人致动力响应分析及在某曲线斜拉桥中的应用

康孝先，华旭刚

(1.绵阳市建设局，四川绵阳621000;2.湖南大学风工程研究中心，湖南长沙410082)

0 引言

随着高强轻质材料使用的增多和对结构形式美学要求的提高，现代人行桥变得越来越轻柔、大跨、低阻尼化。行人步行力荷载是典型的周期性荷载，当荷载频率与结构振动频率相同时，结构就可能发生大幅振动。近年来，一些人行桥发生了由行人荷载引起的大幅侧向振动，严重影响到行人行走的舒适性。最为典型的例子是英国伦敦千禧桥［1］和法国巴黎Solferino桥，这两座桥梁在开放后不久由于发生显著的人致横向振动便被关闭。其中千禧桥的最大横向振幅发生在南跨达到70 mm，对应加速度为0.2～0.25 g，大桥三跨主要的振动频率分别为0.5 Hz、0.8 Hz和1.0 Hz。作为补救措施，随后在这两座桥梁上安装了调谐质量阻尼器和粘性阻尼器。改造工程成本很大，千禧桥的阻尼加固措施耗资约700万美元。日本的T桥也经历了大幅横向振动［2］。1957年，中国的武汉长江大桥(为公路、铁路两用桥梁)由于在开放交通当天有5万人通过，因而发生了大幅度的横向振动。目前，已建成的几个大跨度人行桥均为我国自行设计建设。由于城市化进程，将会建设更多的大跨度人行桥［3］。

本文以一座跨度为200 m的斜拉人行桥为例介绍了人致振动的动力设计的全过程，其中包括步行力荷载模型、横向动力失稳的临界行人数、抑制大幅振动的结构措施和阻尼措施。人致振动响应分析时遵循了德国人行桥设计规范EN03［4］，重点阐述了预测动力失稳临界行人数的三种方法。

1 人行桥的动力设计

1.1 人致动荷载

人在行进过程中，人体重心的左右及上下周期性变化，形成了随时间变化的步行力荷载。这些力有三个方向的分量，即竖向、横向和纵向，力的幅值取决于步长、步频和行走速度等参数。由于正常行走的步行频率是1.8～2.2步/s，所以步行力在竖向的频率大约为1.8～2.2 Hz。侧向力频率为步频的一半，因此侧向力频率介于0.9～1.1 Hz之间。

为便于应用，竖向、横向和纵向步行力荷载Fp(t)统一用傅立叶级数的形式表示:

其中:G为人的体重;αi为第i阶谐波的动载因子(DLF);φi为第i阶谐波相位角;fp为步行力一阶谐波频率，其中竖向及横向步行力一阶谐波频率与步频相等，侧向荷载一阶谐波频率为步频的一半。步行力三个分量的各阶谐波的动载因子DLF可以通过在运动或静止面实测步行力数据导出［2］。步行力的三个分量的简化荷载模型在欧洲、英国和加拿大的设计规范中都有条文说明。

在德国人行桥设计规范EN03中，单位面积上的均布荷载为:

其中:P×cos(2πfpt)是单个步行力荷载的一阶谐波;对竖向力、纵向力和侧向力，P分别取为280 N，140 N和35 N;fp代表步频;n'是荷载作用面上的等效同步行人数:当行人密度为d＜1．0人/m2时，n'当行人密度为d≥1．0人/m2时，n'=1．85为阻尼比;ψ为折减系数，其计算按照图1进行。

值得注意的是人行桥的共振响应在EN03中是按各个模态方式进行计算的。图2为按模态计算的步行力加载图。得到荷载模型后，就可以直接计算最大共振响应:

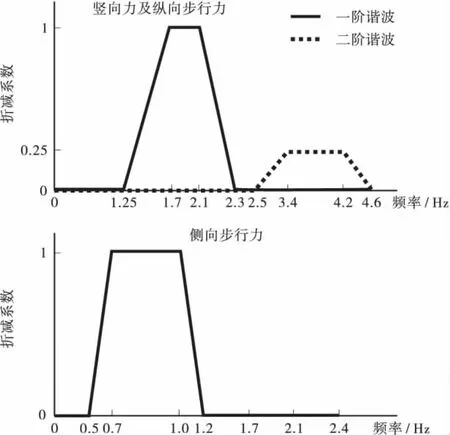
图1 折减系数ψ取值

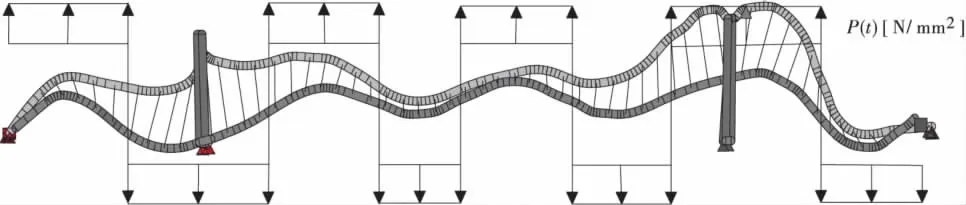
图2 步行力荷载的加载图式

其中:P*为广义步行力荷载，按照式计算;m*和ζ分别是模态质量和模态阻尼比。

1．2 同步横向振动

除了竖向振动，对于大跨度人行桥而言更为重要的是在侧向同步激励作用下的动力失稳。文献中广泛报道的人致振动事件基本上都是横向动力失稳引起的，如英国伦敦千禧桥，法国巴黎的Solferenio bridge和日本的T桥。自伦敦千禧桥事件以来，很多学者对人行桥的横向动力稳定问题进行了研究。

目前，预测人行桥过大横向振动或者研究横向振动的锁定问题主要有三种理论:直接共振理论、相互作用理论和内共振理论。第一种理论认为大幅振动是当行人荷载频率等于人行桥的模态频率时造成的。动力相互作用理论，它基于桥梁运动与桥上行人的运动之间的某种适当的相互作用模型。最后一种理论认为结构的非线性导致桥梁在不同模态间的共振。

Fujino et al.(1993)是首次运用直接共振理论分析了日本T桥的横向振动。他的公式基于模态方法，此公式可以预测人行桥的最大振幅。很多实测表明，当行人数量超过临界值时，可观察横向振动急剧增大。基于这一现象，Dallard et al.(2001)创建了一种相互作用模型来预测导致横向动力稳定的临界行人数量。此模型不能预测振幅，而且还需根据伦敦千禧桥的测试数据来校正参数。Dallard模型在最近人行桥的设计规范中被广泛采用。Nakamura(2003)修订了此模型，加入了振幅自限制特征。我国学者孙利民和袁旭斌不仅考虑了行人的自激特征，而且考虑到造成桥梁强迫振动随意行走的行人。此模型同样需要确定一些自由参数，其取值不太明确。其他不需要选择事前参数的公式主要是Newland(2004)的公式，这一公式是基于行人和人行桥的耦合运动方程而导出的。最后一种理论是由Piccardo提出的，他用这一理论解释了千禧桥的0.48 Hz频率的模态的大幅振动。

1.3 构造与阻尼措施

为了避免人行桥因行人而引起的大幅振动，许多规范建议在设计阶段应该通过修改构造避免人行桥的模态频率控制落入步频范围。这一方法称为频率调整法。对已建桥梁，结构修改往往不可行，最简单的方法就是通过安装外部阻尼装置来增加结构阻尼。应用外部阻尼装置减振是一种有效的措施，并已经有很多工程应用。这些减振措施包括粘滞阻尼器，调谐质量阻尼器(TMD)，调谐液柱阻尼器(TLCD)，调谐液体阻尼器(TLD)。最常用的是粘滞阻尼器和TMDs。

2 德国规范规定的设计步骤

考虑到步行力有固有频率与周期，人行桥的振动本质上可以看成是在步行力谐波作用下的模态叠加响应。在德国规范中，人行桥的设计步骤如下所示:

1)步骤1:确定敏感频率范围。竖向的敏感频率在1.6～2.4 Hz内，侧向在0.5～1.2 Hz内。如果人行桥的模态频率不在这个范围内，在设计阶段不需要考虑行人引起的振动。否则需要详细的评估振动响应来检验是否满足舒适度要求。

2)步骤2:分析人行引起的响应。这个步骤目的在于计算出由行人引起的最大响应，可以用单自由度模态分析或完整的有限元分析。在分析中需要考虑单个行人和一群行人的荷载模型。由上面获得的最大加速度需要满足人体舒适度要求(见表1)。如果不能满足舒适度要求，需要改变结构和安装外部阻尼装置。

表1 人行桥的舒适度指标

3)步骤3:侧向共振失稳人数检验。当侧向加速度超过0.10～0.15 m/s2时，许多行人的步调就会和人行桥的运动一致，导致进一步增强桥的振动，这一过程被称之为侧向动力失稳。因此对侧向频率小于1.2 Hz的人行桥，需要确定行人人数的限值。如果需要，应该安装阻尼装置确保设计行人人数的正常通行。

4)修改结构或安装阻尼装置。通过修改结构和安装阻尼装置，使最大加速度满足人体舒适度要求。

3 曲线斜拉桥的应用

以一个正在建设的曲线斜拉桥为例子来说明行人荷载下动力设计过程。大桥的总长度为400 m。桥的上层是斜拉人行桥，下层为车行桥，其跨度组合为100 m+200 m+100 m。这两部分共用一个索塔。车行桥面主梁采用现浇的预应力混凝土箱梁，人行桥面采用钢箱梁。总共使用了68根拉索，其中52根拉索用于车行桥面，剩余16根拉索用于人行桥面。在原来的设计方案中，人行部分和车行部分之间没有联系。图3显示了人行桥面部分的效果图。

图3 曲线斜拉桥效果图

3.1 原设计方案的振动分析

在桥梁的原设计方案中，人行桥部分和车行桥部分除了共用一个索塔外他们之间没有任何联系。用ANSYS建立了详细的有限元模型并进行模态分析。主要结果归纳如下:

1)第一阶侧弯模态的频率是0.458 8 Hz，为对称性振型;第二阶侧向振动频率为0.731 4 Hz，为反对称振动。这两阶模态频率都位于敏感频率区间，需要检验发生共振时候的共振响应和动力失稳临界人数。

2)第一竖弯模态的频率是0.468 4 Hz，为对称竖弯;第二竖弯模态的频率是0.711 7 Hz，为反对称竖弯。大桥的第14、15、17、18、19、20的模态频率分别为1.620、1.678、1.832、1.960、2.392和2.410 Hz，这些模态频率位于竖向步行力频率范围，即1.60～2.40 Hz，因而也需要验算这些频率的共振响应。

3)对于只有人行桥参与振动模态，其模态质量和阻尼较低，共振时振动较大。

从上面分析可知，本桥的侧弯模态频率非常接近伦敦千禧桥的频率，容易发生振动。但本桥主梁的恒载是48.4 kN/m，达到了伦敦千禧桥的2倍。因此，引发剧烈横向振动的人行桥的临界值大于在伦敦千禧桥相应值。此桥的一个显著特点是曲线桥中存在的三向耦合振动。

在进行共振响应分析时，结构阻尼比假定为0.5%。应用德国规范EN03的方法，计算得到共振条件下最大的竖向和横向加速度为2.776 m/s2和1.463 m/s2，两者都大大超过表2中给出的CL1的加速度的限值。对于两个侧弯模态，应用Dollard和Newland方法进行了动力失稳临界风速预测。结果表明两套方法得到的结果相差很大，Dallard方法得到的结果偏于保守。应用Dallard方法，对称和反对称侧弯模态对应的失稳临界人数分别是220和1 100人。因此，如果满足设计的3 600个行人(按0.5人/m2)，从动态稳定的角度来看最小阻尼比应提高到8.5%和2.0%。

总之，从同时满足行走舒适性和横向动态失稳时模态2、5、14、15、17、18、19和20的最小阻尼比分别为8.5%、2.0%、6.0%、7.5%、1.0%、3.0%、2.0%和3.0%。为达到以上各阶模态阻尼比，设计了7套TMDs减振系统，其总质量高达101.4 t。虽然质量并不大，但控制系统的总费用会很高。此外，如果减振装置失效，人行桥的一小部分可能会导致较大的振动幅度。

3.2 设置链杆装置后的人致振动分析

考虑到人行桥跨度大、柔度小，对原结构进行了一定的结构修改。建议在人行梁和车行梁在主跨用链杆连接。通过参数分析，最后选用一对竖直和一对倾斜的链杆连接人行梁和车行梁，在边跨采用一对水平链杆连接人行梁和车行梁。

通过这个结构改进，第4模态频率(侧弯)是0.986 0 Hz，11，13，14模态频率(竖弯)分别为:1.647，1.885和2.054 Hz。应用同样的方法对这些模态进行了人致振动验算。结果表明，第4，11，13，14模态的最小阻尼比为:4.93%，4.0%，1.0%，2.5%。达到上述阻尼比所需的总调频质量阻尼器质量为42.29 t，只占原设计的40%，预计控制系统的支出将会显著减小。每个调频质量阻尼器的详细参数见表2。

表2 所有调谐质量阻尼器的模态参数

4 结论

人行桥的动力设置旨在通过修改结构设计和安装附加的阻尼装置来降低桥梁的振动加速度，已日益成为现代低频和低阻尼人行桥设计不可缺少的一部分。本文简述了人行桥动力设计过程的主要方面，包括步行力荷载模型、动力失稳临界行人数和抑制大幅振动的结构措施以及阻尼措施。重点描述了预测人致横向动力失稳的三种方法。以国内一座200 m主跨的人、车桥面分离的桥梁为例，阐述了动力设计全过程。

［1］P.Dallard，A.J.Fitpatrick，A.R.Flint，et al.The London Millennium footbridge［J］.The Structural Engineer，2001，79(22):17-33.

［2］Y.Fujino，M.Pacheco，S.Nakamura.Synchronization of human walking observed during lateral vibration of a congested pedestrian bridge［J］.Earthquake Engineering and Structural Dynamics，1993，22(7):741-758.

［3］陈政清，华旭刚.人行桥的振动与动力设计［M］.北京:人民交通出版社，2009.

［4］HiVoSS(2008).Human induced vibrations of steel structures:design of footbridges-guidelines，RFS2-CT-2007-00033，Research Fund for Coal＆Steel.

［5］K.Nakamaura.Lateral Vibration of Footbridge by Synchronised Walking［J］.Journal of Constructional Steel Research，2006，62(11):1148-1160.

［6］D.E.Newland.Pedestrian Excitation of Bridges［J］.Mechanical Engineering Science，2004，218(4):477-492.