基于极限分析的二级边坡稳定性分析方法研究

易建章

(湖南省交通科学研究院，湖南长沙410015)

0 引言

随着交通事业的蓬勃发展，在各种高速公路及铁路建设中，出现了较多的边坡工程。某些边坡工程很可能因失稳而发生滑坡，大规模的滑坡轻则中断交通、破坏农田，重则对群众的生命财产造成重大损失［1-3］。因此，对边坡进行快速准确的稳定性分析，是日益重要的研究课题。

目前对简单边坡的稳定性分析研究较多，而对二级或者多级边坡稳定性分析研究较少。而在实际工程中，随着高边坡的大量出现和施工条件的限制，往往采取多级边坡的方式确保边坡的稳定性并提高坡率，减少边坡占地面积。孙栋梁等［4］一般将多级边坡简化成低阶或单级边坡来进行稳定性分析。时卫民等［5］在假定多级边坡滑动面为直线的前提下，基于传统稳定性系数理论，得到了多级边坡安全系数的表达式。目前的研究方法均在一定假定下对边坡进行稳定性分析，忽略了多级边坡自身的复杂性。

本文运用极限分析上限法对坡顶存在一定倾角及超载的二级边坡稳定性进行研究，并分析各个参数对该类边坡安全系数的影响。

1 计算原理

对于任意假想的破坏机构，如果土体自重所做的功率超过了内部能量耗损功率，那么边坡就会因自重而引起破坏。因此，对于这类机构，使外功率与内部耗损功率相等，即可得到临界高度的一个上限值［6］。

如图1所示二级边坡，在该图中，对数螺旋滑动面通过坡趾下方，该破坏机构由三个变量θ0，θh，D/r0控制。该边坡为各向同性的均质边坡，为得到临界高度，首先需要对外功率及内部耗损率进行计算。

直接从AA'CB'BA区域积分计算土重所做的外力功率非常不便。现通过一种较为简单的方法，即分别计算出OABO，OB'BO，OCB'O，OA'CO及OAA'O区中土重所做的外功率W1，W2，W3，W4和W5。经化简可得土重所做的外功率W0为:

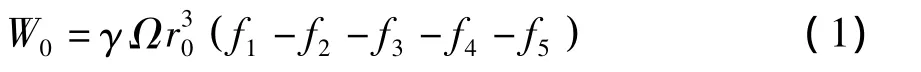
式中:

OB'BO，OCB'O，OA'CO及OAA'O区域得到的函数f2，f3，f4和f5的表达式为:

图1 对数螺旋破坏机构

坡顶荷载q的取值所做外部功率为:

内部能量耗损发生在间断对数螺旋破坏面AB上，可以由该面的微分面积r dθ/cosφ与粘聚力c以及与跨该面的间断速度V cosφ连乘后，在沿整个AB面积分，即可得到总的内部能量耗损率:

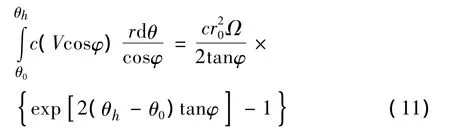
式中f(θ0，θh，D/r0)定义为:

边坡稳定性分析一般可以基于强度储备的安全系数［7］，即降低岩土体强度来保证边坡的稳定性，经折减的剪切强度参数cf和φf变为:

式中，cf和φf为折减后的抗剪强度参数;c和φ为原始抗剪强度参数;K为安全系数。

在工程实际中，α1、α2、β1、β2、γ、c、φ及边坡高度H已知，经过强度折减后，将折减后的强度参数cf和φf代入式(11)中，计算出强度参数折减后的边坡的临界高度Hcr［8］，令Hcr=H，可得:

式中，f1、g2、g3、g4、g5及H/r0中的摩擦角φ均为φf=arctan(tanφ/K)所代替。记:

当θ0，θh和D/r0满足条件:

时，函数f(θ0，θh，D/r0，K)有一个最小值，即最小上限。将满足式(16)的相应的θ0，θh和D/r0值代入式(14)即可得到边坡安全系数K的一个上限解。

2 参数影响及对比分析

目前边坡稳定性分析主要方法有极限平衡法、强度折减有限元法及极限分析法等［9，10］。为体现本文方法的有效性，分别选取若干算例进行分析(见表1)。以下算例中β1=β2。

表1 不同强度参数c，φ下安全系数计算值

当c=25 kPa，φ=10°～20°时，安全系数的计算结果如图2—a所示;当φ=20°，c=10～25 kPa时，安全系数的计算结果如图2—b所示。

图2 强度参数c、φ对安全系数的影响

浙江省开化某国道二级边坡，边坡主体主要由坡残积层及强风化层组成，局部夹强至中风化岩体，在地质构造作用下，具有强烈风化软弱带，其产状倾向坡面，在边坡开挖切削坡脚支撑并致使其软弱带临空暴露的情况下，极易产生上覆风化岩土体沿其下伏基岩较大规模的滑动变形和破坏。具体参数为:c=20 kPa，φ=20°，α1=1/3，α2=2/3，β1=10°，β2=45°，γ=19 kN/m3，H=12 m。经计算，采用传统极限平衡法得到安全系数K1=1．328;强度折减有限元法及极限分析获得的安全系数K2=1．386;而本文方法计算出的安全系数K3=1．296。因此，由计算结果可知，采用本文方法分析边坡稳定性是有效的。

3 结论

本文将强度折减技术与极限分析上限定理相结合，对多级均质边坡进行了稳定性分析，通过算例，论证了本方法的有效性。针对二级的边坡，运用本文方法进行稳定性分析能够得到令人较为满意的结果。但本文方法是对均质边坡进行的稳定性分析，但实际中边坡一般为非均质，同时也没有考虑水压力、坡顶荷载等外界因素对边坡稳定性的影响，因此本方法还待进一步的研究与完善。

［1］韩龙，肖碧，徐世春.公路边坡防治动态信息化的重要性［J］.岩石力学与工程学报，2003，22(增2):2725-2726.

［2］张有天，周维垣.岩石边坡的变形与稳定［M］.北京:中国水利出版社，1999.

［3］李亮，于广明，褚雪松，等.土坡稳定极限分析上限法中的多解性分析［J］.岩土力学，2009，30(增2):97-98.

［4］孙栋梁，侯克鹏，杨春丽.阶梯形边坡简化计算的研究［J］.矿业研究与开发，2005，25(4):18-19.

［5］时卫民，叶晓民，郑颖人.阶梯形边坡的稳定性分析［J］.岩石力学与工程学报，2002，21(5):698-701.

［6］陈惠发.极限分析与土体塑性［M］.北京:人民交通出版社，1995.

［7］王根龙，伍法权，李巨文.折线型滑面边坡稳定系数计算的极限分析上限解［J］.水文地质工程地质，2007，34(1):62-65.

［8］乔丽平，王钊.加筋土坡临界高度的研究［J］.岩石力学，2006，27(1):132-136.

［9］程祖煜.土质边坡稳定性分析—原理、方法、程序［M］.北京:中国水利水电出版社，2003.

［10］郑颖人，赵尚毅.有限强度折减法在土坡与岩坡中的应用［J］.岩石力学与工程学报，2004，23(19):3381-3388.