变质板岩高边坡岩石蠕变特性试验研究

曾伟军

(湖南省炎汝高速公路建设开发有限公司，湖南炎陵412500)

0 引言

道路工程建设必然会遇到路堑边坡开挖问题，为了保证道路施工和工后运营安全，要求边坡不仅在施工期是安全的，而且要求在运营期内也是稳定的。这就要求边坡在设计过程中考虑其长期稳定问题。实际工程中，很多边坡在设计的时候达到了规范要求的安全系数，却并不意味这些边坡就是永久安全稳定的，这是因为边坡岩体存在流变特性。

自1939年Griggs发现当作用岩石试样上的荷载达到破坏荷载的12.5%～80%时，砂岩、泥板岩和粉砂岩等岩石就会发生蠕变现象，此后几十年人们从各个方面进行了不同种类岩石蠕变试验研究，如国外一些学者［1～3］对粘土岩、盐岩、软岩等岩类进行的蠕变试验，分析其蠕变曲线规律及相应的蠕变本构方程。国内的部分学者［4，5］则对花岗岩、大理岩等进行了单轴压缩与三轴压缩蠕变试验，分析该类岩石的蠕变特性建立相应的蠕变本构模型。国内研究过去多数是对于硬岩的蠕变规律进行探讨，如今大多学者逐渐开展了对软弱岩石压缩或岩体剪切蠕变的研究，袁海平等［6］采用改进的伯格斯黏弹塑性模型方程对软弱复杂矿岩进行了单轴压缩蠕变试验。谌文武等［7］对红层软岩不同含水率条件下岩石试样进行了岩石蠕变试验。陈绍杰等［8］从微观角度对某矿煤岩在MTS岩石伺服试验机上进行了蠕变试验。由上述可知，虽然国内外在硬岩和软岩的蠕变规律已经开展了较多和较深入的研究，但是很少见有对板岩进行蠕变试验的报导，且由于区域地质运动等因素并不能完全将前人对软岩的蠕变规律结果应用到研究的板岩对象上，故本文拟开展对板岩蠕变特性的研究，目的是认识该类岩石的蠕变规律，以及建立相应的蠕变本构模型和方程并求出模型参数，为板岩高边坡长期稳定性分析提供可靠的岩石参数。

1 板岩蠕变试验

1.1 试验设备及试样制备

采用RYL—600微机控制岩石剪切流变仪在流变实验室进行板岩的蠕变试验，该流变仪主要用于岩石和岩石弱面的流变试验。

本次试验岩样取自钻孔岩芯，经高精度切割、打磨，成型后的试样规格见表1。试样端面平整度和侧面平整度控制在0.03 mm，试样中心线与端面的垂直度误差小于0.25°。试验采用单轴压缩分级增量循环加载，各级加载所持续的时间根据试件应变速率变化情况予以确定，即当试样的轴向变形在24 h内小于0.01 mm，认为其变形基本稳定，再进行下一级荷载的循环，依此类推逐级循环。本次试验分两组进行加载，一组加载级别为:0→1 MPa→2 MPa→3 MPa→4 MPa;另一组加载级别为:0→0.5 MPa→1 MPa→1.5 MPa→2 MPa→2.5 MPa→3 MPa→3.5 MPa→4 MPa。

表1 蠕变实验试件尺寸记录

1.2 试验结果及数据整理

板岩单轴压缩蠕变曲线如图1所示。

图1 板岩单轴压缩蠕变试验曲线

由图1可知，板岩的蠕变曲线具有弹性、粘性共存的特性，故其单轴压缩下总应变ε包括可恢复的瞬时弹性应变εme、不可恢复的瞬时塑性应变εmp、粘弹性应变εce和粘塑性应变εcp四部分组成［9］，即:

具体到各分级加载，在本级应力σi施加的瞬间，实际测到的瞬时应变值应由瞬时弹性应变值和瞬时塑性应变值组成，公式如下:

同理，在本级应力σi作用过程中试件的蠕变应变值也由下列两部分组成:

第i级荷载作用下产生的瞬时应变为:

由上述可知，对于第i级荷载作用下试件的应变值，公式(1)可写成:

由图1并按上述数据整理方法对试验数据进行整理，可得试件1和试件2、试件3和试件4在各级荷载作用下的瞬时应变增量、瞬时应变、蠕变应变随轴向应力等级的关系曲线(分别如图2、图3、图4)。

图2 瞬时应变增量—轴向应力σ关系曲线

图3 瞬时应变)—轴向应力σ关系曲线

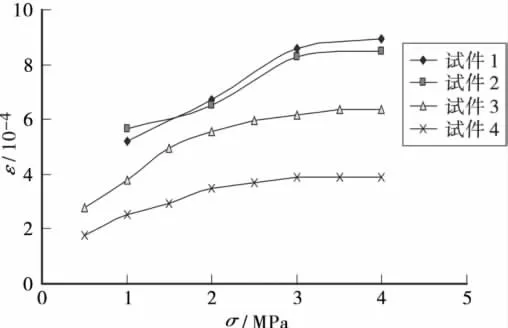
图4 蠕变应变)—轴向应力σ关系曲线

4)由图2可知，试件在加载各级荷载的瞬间，板岩产生瞬时压缩应变，随后应变随时间增长而逐渐增长，产生了明显的蠕变变形。不论轴向应力处于较低或较高状态，每级荷载作用下试件蠕变变形的速率都随时间的增长而逐渐缓慢，当达到一定时间后，变形增长变得很小，甚至不再增长，可以认为板岩的最终变形趋于一个稳定值。

5)以试件1为例(见图5)，对于第1分级加载蠕变率在t=8 h时就很快衰减接近0，随后保持不变，其蠕变性能并不明显。而对于第2分级荷载，蠕变率在t=15 h才衰减至稳定值，对于第3、4分级加载，蠕变率要经过更长一段时间后才接近于0，且随着分级荷载的增加，蠕变达到稳定的时间也越长。

图5 试件1分级加载蠕变率曲线

2 蠕变模型分析及参数确定

2．1 蠕变模型分析［9］

目前常见的蠕变模型有三种:马克斯威尔模型、开尔文模型、博格斯模型。根据对蠕变试验数据的整理与分析，以及对蠕变曲线规律的认识:曲线一开始为瞬时变形，然后应变按指数递减规律的速率增长，最后保持或接近恒定速率增长。可以认为板岩蠕变具有以下两方面的特点:①板岩蠕变前期与开尔文(Kelvin)元件代表的蠕变曲线吻合，可以用开尔文(Kelvin)元件来模拟该时期蠕变性质;②板岩蠕变后期与马克斯威尔(Maxwell)元件代表的蠕变曲线吻合，可以用马克斯威尔(Maxwell)元件来描述该时期蠕变性质。因此，总体上可以用开尔文元件和马克斯威尔元件串联组成的伯格斯(Burgers)模型(见图6)来模拟板岩的蠕变特征。

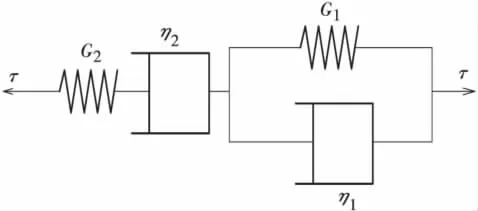
图6 伯格斯模型示意图

伯格斯模型是由开尔文模型和马克斯威尔模型通过串联形式组成的。因此，伯格斯体在受到单轴压应力作用时产生的应变是由马克斯威尔体应变和开尔文体的应变之和可以得到伯格斯体在受到轴向应力σ1时的轴向应变ε1(t)为:

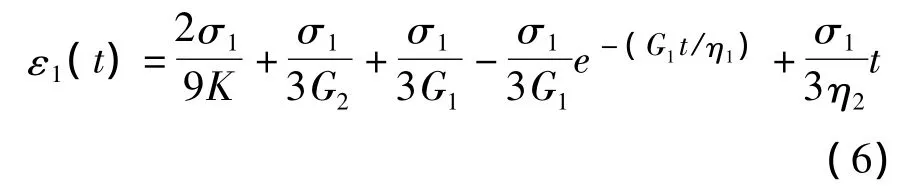
式中:G1、η1为开尔文体的剪切模量和粘滞系数;G2、η2为马克斯威尔体的剪切模量和粘滞系数。

2．2 板岩蠕变参数确定

伯格斯模型中的四个参数η1、η2、G1、G2可采用下列方法确定。

当t=0时，认为蠕变曲线在纵轴上的截距大小表示瞬时弹性应变εe值:

当t足够大时，应变速率可近似认为一常数，蠕变曲线则可近似认为一直线。该直线延长线在纵轴上的截距大小为εa值。

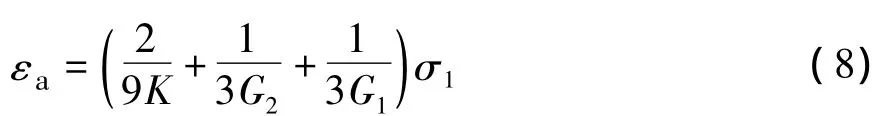
该直线斜率为ma。

由式(9)可确定参数η2。

考虑实际试验时往往不能瞬时施加荷载，所以在实用上还需采用以下方法求得瞬时弹性应变εe。q(t)为蠕变试验曲线与直线延长线(第二期蠕变曲线的渐近线)间的垂直距离。

对式(10)两边取自然对数，有:

在半对数格纸上绘出ln(q)与t的关系曲线，式(11)表明ln(q)与t的函数关系为一直线，该直线在纵轴上的截距为εq，斜率为mq。

由式(12)、式(13)可以确定参数G1和η1。

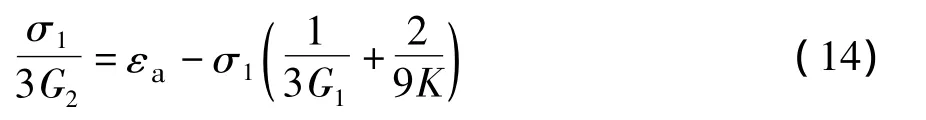
所以:

由于试验数据量偏大，仅以试件3为代表。根据上述方法，图7以及表2给出了计算过程，其中通过板岩的压缩变形试验得出了该板岩高边坡岩石的弹性模量和泊松比(E=1.02 GPa，μ=0．35)。试件3在不同应力水平作用下伯格斯模型参数见表3。

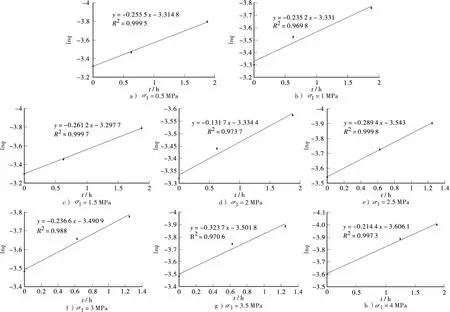
图7 t-ln q关系曲线(试件3)

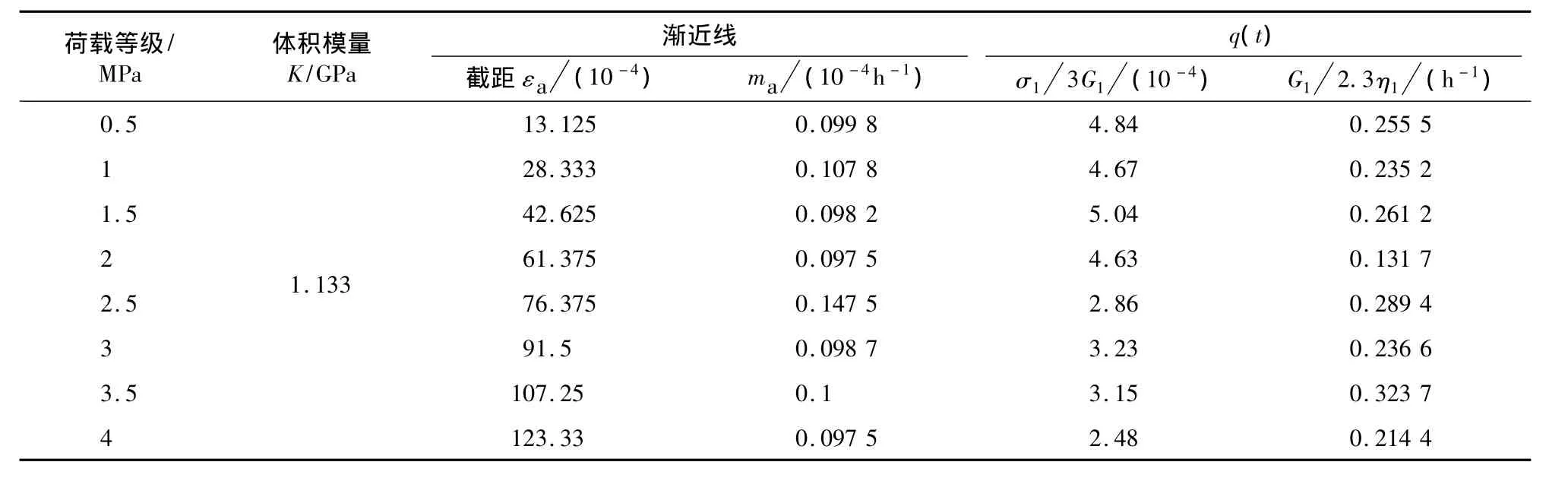
表2 板岩的蠕变(试件3)

表3 试件3伯格斯模型参数

由表3可知，随着每级荷载的增大，伯格斯模型各参数都有减小的趋势，但是G2的变化很小，可忽略不计，而G1、η1、η2的值则逐渐减小，说明板岩的蠕变随着轴向应力的增大，蠕变应变表现越来越明显。因此，板岩蠕变性质为非线性粘弹性。这些变形常数具有实际上的物理意义:G2是弹性剪切模量;G1控制着迟延弹性的数量;η1决定着迟延弹性的速率;η2描述粘滞流动的速率。

3 结论

1)每级荷载产生的瞬时应变增量在实验开始阶段都有增大的趋势，主要是由于细微裂隙受压闭合造成的。随着荷载的继续增加，细微裂隙不再闭合，而承受轴向应力的岩石颗粒由于硬化则表现为逐渐减小。试件在各级应力作用下产生的瞬时应变与轴向应力大小成线性比例增长。

2)以试件1为例，对于第1分级加载，蠕变率在t=8 h时就很快衰减接近0，随后保持不变，其蠕变性能并不明显。而对于第2分级荷载，蠕变率在t=15 h才衰减至稳定值，对于第3、4分级加载，蠕变率要经过更长一段时间后才接近于0，且随着分级荷载的增加，蠕变达到稳定的时间也越长。

3)试件在加载各级荷载的瞬间，板岩产生瞬时压缩应变，随后应变随时间增长而逐渐增长，产生了明显的蠕变变形。不论轴向应力处于较低或较高状态，每级荷载作用下试件蠕变变形的速率都随时间的增长而逐渐缓慢，当达到一定时间后，变形增长变得很小，甚至不再增长，可以认为板岩的最终变形趋于一个稳定值。

4)随着每级荷载的增大，伯格斯模型各参数都有减小的趋势，说明板岩的蠕变随着轴向应力的增大蠕变应变表现越来越明显。因此，板岩蠕变性质为非线性粘弹性。

［1］Aubertin M.Constitutive equations with internal state variables for the inelastic behavior of soft rocks［J］.Appl.Mech.Reviews，ASME(1994)47(6-2):97-101.

［2］Hunsche，U.Result and interpretation of creep experiments on rock salt.Themechanical behavior of salt［C］，Proc.1st Conf.Eds.H.R.Hardy，Jr.，and M.Langer，Trans Tech Publ.，Clausthal-Zellerfeld，1984.

［3］Yongsheng Li，Caichu Xia.Time-dependent tests on intact rocks in uniaxial compression［J］.Rockmechanics andmining sciences，2000，137:178-186.

［4］李铀，朱维申，等.风干与饱水状态下花岗岩单轴流变特性试验研究［J］.岩石力学与工程学报，2003，22(10):1673-1677.

［5］李化敏，李振华，等.大理岩蠕变特性试验研究［J］.岩石力学与工程学报，2004，23(22):3745-3749.

［6］袁海平，曹平，万丈，等.分级加卸载条件下软弱复杂矿岩蠕变规律研究［J］.岩石力学与工程学报，2006，25(8):1575-1582.

［7］谌文武，原鹏博，刘小伟.分级加载条件下红层软岩蠕变特性试验研究［J］.岩石力学与工程学报，2009，28(1):3077-3083.

［8］陈绍杰，郭惟嘉，杨永杰.煤岩蠕变模型与破坏特征试验研究［J］.岩土力学，2009，30(9):2595-2600.

［9］徐志英.岩石力学［M］.北京:中国水利水电出版社，1993.