电驱动低温空气源双作用行波热声热泵
2012-02-26罗二仓余国瑶
杨 卓 罗二仓 余国瑶 赵 阳 周 远
(1中国科学院低温工程学重点实验室 北京 100190)(2中国科学院研究生院 北京 100049)
1 引言
随着资源和环境问题的日益突出,“节能减排”已经成为一个世界性问题。空气源热泵由于其初期投资低、安装方便、无需辅助热源等优点,逐渐引起了人们的重视[1-2]。但是,常规的空气源热泵在室外低温工况下运行时会出现压比增高、容积效率下降、制冷剂质量流量减少、供热能力下降、压缩机排气温度过高等问题。冬季时,常规空气源热泵在中国的哈尔滨和长春(室外温度-20℃左右)运行压缩比接近20(压缩机最佳压比一般在3.5—4.0水平)。以上问题严重制约了常规热泵在寒冷地区的发展[3]。众多学者对常规热泵进行了各种改进,例如:20世纪80年代初Nobukatsu Arai提出了带闪发器的涡旋压缩机注气系统,Hagimoto K等人提出采用带喷液旁路的涡旋压机系统来解决低温工况制热时排气温度过高的问题,后有日本公司推出了成熟的产品[4-6]。20世纪80年代中期有学者提出带经济器的准二级压缩系统[7-8],但这些研究都没有从根本上解决环境温度低时,热泵压比过高的问题。这个问题是常规热泵本身的热力循环所造成的。20世纪末期诞生了一种被称为“热声热机”的新型热机(包括热声发动机和热声制冷机)[9],它基于热声效应-热能与声能的相互转换,其优点包括完全无运动部件、可靠性高、寿命长、可利用低品位能源和环保等[10-13]。热声热机属于一种交变流动热机,其内部流体经历的热力过程完全不同于稳态流动的热机[14]。这为解决低温下常规热泵压比过大的问题提供了全新的思路。在这个基础上,本文提出一种全新双作用行波热声热泵,该热泵由直线压缩机驱动,工作在超低环境温度下进行。本文对其在不同工况下(特别是低温环境下)的泵热性能进行了理论研究。
2 电驱动低温环境双作用行波热声热泵流程
双作用的概念源于双作用斯特林热机,双作用是指压缩活塞与膨胀活塞同时集于一个活塞,该活塞前后端面分别起到压缩和膨胀的作用。但是常规双作用斯特林热机一般由曲柄连杆机构驱动,气缸活塞摩擦大,密封困难,一直存在可靠性不高等致命问题。新型的双作用行波热声热泵系统结构简图如图1。该系统由3个完全相同的部件组成。每一个部分都包括直线压缩机、次低温换热器、热缓冲管、高温换热器、回热器及主低温换热器。每个热泵的工作状态都完全一致,因而3个热泵的边界具有周期性,两两之间相同位置的波动压力及体积流率的相位差为120°,因此系统能够方便地实现结构调相。双作用行波热声系统的最大特点有两个:(1)使用热缓冲管,解决斯特林系统中膨胀活塞必须位于低温温区的问题;(2)采用无摩擦、寿命高的直线压缩机,整个系统形成了一种高效转换的共振系统。通过调节直线压缩机的输入电压可以容易调节制冷容量,可达到无极调节的水平。

图1 双作用低温热泵结构图Fig.1 Schematic diagram of double-acting traveling-wave thermoacoustic heat pump
3 低温双作用热泵的优化计算
3.1 设计工况
本实验室已经研制了一种双作用直线压缩机,其谐振频率在80 Hz附近,工作压力为5 MPa。为了与该直线压缩机匹配,热泵设计工作频率也定为80 Hz,平均压力5 MPa,工质采用氦气。热泵入口处直线压缩机的振动位移幅度为6.5 mm。考虑到空调供暖和生活热水的供应,热泵高温换热器温度设计温度为50℃。考虑到北方地区冬天的室外环境温度,热泵低温换热器温度定为-20℃。
3.2 理论模型和计算方法
本计算采用美国Los Alamos国家实验室编写的DeltaEC 6.2程序进行模拟计算。该程序是基于热声理论建立和编写的,即在指定的几何边界条件下对动量方程、连续性方程和能量方程进行积分,得到压力波动、体积流率及温度分布。根据计算得到的波动量、热力参数后,可以评价热声系统的转换性能。
DeltaEC中的积分方程为式(1)—式(4):


式中:p1为波动压力,U1为体积流率,Tm为平均温度,H·tot为总能流,pm为平均压力,ω为系统工作频率。DeltaEC提供了超过200种几何结构模块,不同模块根据实际情况对波动方程和能量方程进行了相应的简化。
该系统中的双作用行波热声热泵由3个相同的直线压缩机驱动3个相同的热声热泵。由于结构的对称性,只需要计算其中的一个模块就可以评估系统的制热性能。对于每个热声热泵单元,其制热量Qh就是高温换热器6进出口的总能流之差。而该热泵消耗的声功则为该热声热泵系统进出口的声功之差:W=Win-Wout。制热系数为:COPh=Qh/(Win-Wout),相对卡诺系数(或热力完善度)为:η=COPh/(Th/(Th-Tc))。
3.3 优化方法
由于3台热泵完全对称,所以取其一进行优化。热泵的换热器均采用板叠式换热器,回热器采用丝网填充。可优化变量包括各部件的长度和直径,换热器的板叠间距和孔隙率,丝网的目数和丝径。对于单台热泵,有23个可优化变量。其中影响较大的量为:工作频率,平均工作压力,回热器丝网、长度、直径、孔隙率,换热器长度、直径、板叠间距、孔隙率。影响较小的量为:热缓冲管壁厚,次低温换热器的尺寸。先考虑整个热泵直径不变,可优化变量减少为17个,再除去影响较小的量,变量减少为13个。
优化流程:
(1)在工作频率80 Hz,平均压力5 MPa的条件下,将热泵所有的参数设定在较为合理的值,得到最初模型;
(2)计算不同管径,寻求一个效率与泵热量都较高的点;
(3)选取一种丝网(丝径和目数);
(4)优化回热器长度;
(5)优化高温换热器和主低温换热器的板叠间距;
(6)优化高温换热器及主低温换热器长度;
(7)转到D,直到效率不再有显著提高;
(8)优化热缓冲管的长度及连接管长度;
(9)转到C,得到效率最高的一种丝网;
(10)优化影响较小的变量。
这样就获得了80 Hz平均压力5 MPa等直径条件下满足要求的热泵,据此再进一步计算各部件不同直径下的情况,获得最优的热泵。
3.4 优化计算的结果
通过优化流程,在设计工况下获得了单台COPh为2.93、相对卡诺效率为63.54%、泵热量为1 574.2 W的热泵,关键结构尺寸见表1。直线压缩机的效率通常为0.7—0.9,也就是整个系统的COPh在2.01到2.64之间,而通常当环境温度低于-10℃,常规热泵的COPh不大于2。只需要将直线压缩机之间的相位差由-120°调整为120°,该热泵就能在制冷工况下运行。此时,热泵的高温换热器变成了制冷机的冷端换热器。在环境温度35℃,制冷温度10℃时,热泵的 COPc为 4.07。即整个系统的 COPc在2.85—3.66,也高于目前常见家用空调COPc。

表1 双作用行波热声热泵的主要结构参数Table 1 Dimensions of double-acting traveling-wave heat pump
4 低温双作用热泵在不同运行工况下运行状态
用户对热量大小有不同的需求,外界环境的温度也时刻发生着变化,这导致热泵不总是在额定工况下运行。所以,对新型热泵不同的运行工况进行了模拟,以预测其变工况工作性能。在热泵的运行过程中,为了满足不同的泵热量需求,通常通过调节压缩机的运行频率和压缩机的活塞位移来达到目的。在使用过程中,不仅低温换热器温度是变化的,高温换热器的温度通常也不是固定的。希望低温双作用热泵能够适应各种工作条件,所以也计算了不同换热器温度下热泵的运行参数。
4.1 运行频率的影响
图2、图3给出了低温双作用热泵在不同工作频率(20 Hz到90 Hz)下的运行的计算结果。因为压缩机的活塞移位和系统内空体积的大小是不变的,变化的仅仅是系统运行频率,所以系统压比变化应该较小。由图2可见,系统运行频率增大,入口压仅变化了0.48%。由图3知,随着运行频率增大,系统的相对卡诺效率从74.583%下降到了61.748%,下降了17.2%;而系统的泵热量由364.71 W上升到了1 779.7 W,上升了388.0%。由此可见,通过调节系统工作频率系统可以在效率变化较小的情况下,较大幅度地调节泵热量。

图2 热泵入口压比随运行频率的变化曲线Fig.2 Pressure ratio at inlet vs.frequency

图3 泵热量和相对卡诺效率随运行频率变化曲线Fig.3 Efficiency and heating capacity vs.frequency
4.2 压缩机活塞位移的影响
由于活塞的面积是固定的,所以压缩机活塞位移的改变对热泵的影响其实是通过热泵入口处体积流率V1的改变来实现的。80 Hz的运行频率时,3 mm的活塞位移对应着V1=6.66×10-3m3/s,10 mm的活塞移位对应着V1=2.2×10-2m3/s。图4、图5给出了系统工作状态是如何随入口体积流率改变而改变的。对于其余参数都不变的热泵系统,入口处的压比变化应随入口处体积流率近似呈线性变化。图4显示,入口处压比和入口处体积流率的变化的确近似呈线性变化。由图5可见系统的相对卡诺效率随入口体积流率增加,先增大后减小,在体积流率为1.103 2×10-2m3/s处到达最大值64.6%,对应活塞位移为4.98 mm,此时的泵热量为889.53 W。热泵的泵热量随入口体积流量增大显著增大,泵热量从291 W增大到了3 821.1 W。可以通过调节压缩机外接电路,改变直线压缩机的输入电压,从而达到改变压缩机的活塞位移无级调节泵热量的目的。

图4 热泵入口压比随入口体积流率变化曲线Fig.4 Pressure ratio at entrance changes with inlet volume flow rate
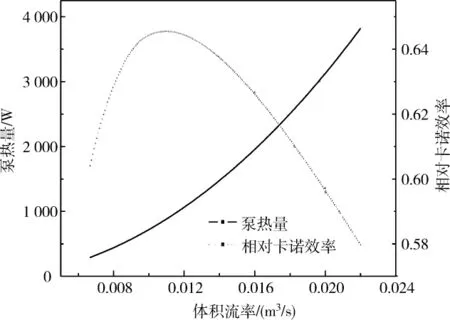
图5 泵热量与相对卡诺效率随入口体积流率变化曲线Fig.5 Efficiency and heating capacity changes with inlet volume flow rate
4.3 换热器温度
图6给出了当高温换热器温度固定在323 K时,计算了低温换热器温度从233 K上升到273 K系统运行参数的变化。图7给出了当低温换热器温度固定在253 K时,计算了高温换热器温度从303 K上升到343 K系统运行参数的变化。计算结果表明,高温换热器和低温换热器的温度变化对热泵入口压比和热泵的泵热量的影响均较小。例如:高温换热保持323 K,低温换热温度从273 K下降到233 K时,系统压比从1.187 7上升到1.190 5,系统泵热量从1 562.8 W上升到了1 585.4 W。低温换热器保持253 K不变,高温换热器温度从303 K上升到343 K,系统压比从1.188 2上升到了1.189 8,泵热量从1 564.1 W上升到1 584.3 W。这就意味着换热器温度的改变对系统的运行状态影响不是太大。图8给出了低温为253 K时两种高温时热泵内部压力波和速度波相位分布情况。图9给出了低温为253 K时两种高温情况下热泵声功流分布情况。由图6、图7发现,当高温换热器温度升高时或者低温换热器温度降低时,热泵的相对卡诺效率反而略微升高。原因可能有二:(1)虽然系统压比和体积流率随着温差的增大没有太大变化,但是由图8知,高温换热器温度升高20 K,入口处体积流率与压力波动的相位差由54.7°变化到了53.9°,所以入口声功从1799.6 W上升到1 844.4 W,即直线压缩机的输出功率变大了(如图9)。又因为系统的波动压力和体积流率变化不大,所以阻力损失所占比例变小。(2)温度改变后,回热器效率更高(计算方法参考文献[15])。高温换热器温度为323 K时,制冷系数 NTACOP为3.51,高温换热器为353 K时,制冷系数NTACOP为2.77,分别除以其极限效率得到76%和78%,说明回热器的相对效率有所提升。低温换热器温度降低相对卡诺效率升高的原因与此类似。
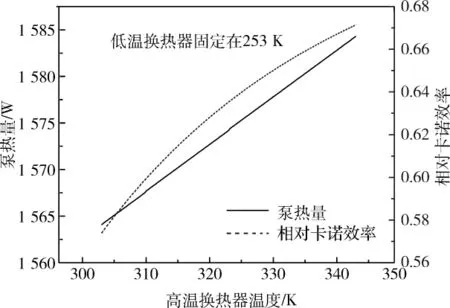
图6 热泵泵热量与相对卡诺效率随高温换热器温度变化曲线Fig.6 Heat pumping capacity and relative Carnot efficiency changes with temperature of high-temperature heat exchanger

图7 热泵泵热量与相对卡诺效率随低温换热器温度变化曲线Fig.7 Heat pumping capacity and relative Carnot efficiency changes with temperature of low-temperature heat exchanger

图8 热泵内部压力波动与体积流率相位角Fig.8 Phase distributions of pressure and volume flow waves inside heat pump
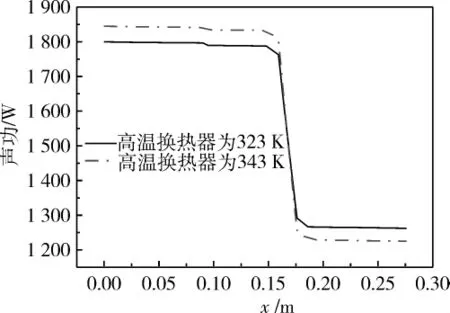
图9 热泵内部声功流Fig.9 Acoustic power flux inside heat pump
5 结论
通过DeltaEC的优化计算,设计了一台与现有直线压缩机相匹配的低温双作用行波热声热泵。在环境温度-20℃,供热温度50℃的条件下,热泵入口的压比为 1.19,COPh为 2.93,相对卡诺效率为64%,泵热量为4 722.6 W(单台1 574.2 W)。计算模拟了热泵在不同工况下运行的表现,发现通过调节压缩机频率和活塞位移系统能很容易在热泵效率改变较小的情况下调节泵热量。通过改变压缩机活塞运动的相位差,系统能很容易实现制冷,并且制冷时系统的COPc也超过一般常规家用空调。低温双作用行波热声热泵能够克服常规热泵在环境温度低于0℃时压比过大的问题。这是因为热声泵热原理不同于常规的热泵,在低温换热器温度下降或者高温换热器温度上升时,系统压比和泵热量变化均很小,且相对卡诺效率略有提升。而且,该热泵与常规热泵相比在温差较大时更有优势。若采用规整流道的板叠式回热器及换热更好的管壳式换热器,双作用行波热声热泵的效率和泵热量可能进一步提升。计算结果表明双作用行波热声热泵在低环境温度的情况下具有压比低、效率高、泵热量易调节等优点,非常有潜力成为一种高端热泵技术。
1 范存养.空气热源热泵的应用与展望[J].暖通空调,1994(6):20-24.
2 龙惟定.试论中国的能源结构与空调冷热源的选择取向[J].暖通空调,2000,30(5):27-32.
3 马最良,杨自强,姚 杨,等,空气源热泵冷热水机组在寒冷地区应用的分析[J]. 暖通空调,2001,31(3):38-31.
4 Afjei Th,Suter P,Favrat D.Experimental analysis of an invert-driven scroll compressor with liquid injection[A].Proceedings of International Compressor Engineering Conference at Purdue,1992(2):541-550.
5 Yanagisawa T,Fleming John S,Dutta A K,et al.A study of a refrigerant cycle driven by a liquid refrigerant injected compression[A].Proceedings of the ASME Advance Energy System Division,1997,337:295-302.
6 Asit K Dutta,Tadashi Yanagisawa,Mitsuhiro Fukuta.An investigation of the performance of a scroll compressor under liquid referigerant injection[J].Inter Journal of refrigeration,2001,24:577-587.
7 Zhang Jianyi.Super-subcooling with R12&R22 refrigeration plants using reciprocating compressors[J].Applied Energy,1993,45(2):157-166.
8 Steven Jonsson.Performance simulations of twin-screw compressors with economizer[J].International Journal of Refrigeration,1991(14):345-350.
9 Wheatley J C,Cox A.Natural engines[J].Physics Today,1985:38-50.
10 Chen Guobang,Tang Ke,Jin Tao.Advances in thermoacoustic engine and its application to pulse tube refrigeration[J].Chinese Science Bulletin,2004,49(13):1319-1328.
11 Hu Jianying,Luo Ercang,Li Shanfeng,et al.Heat-driven thermoacoustic cryocooler operating at liquid hydrogen temperature with a unique coupler[J].Journal of Applied Physics,2008,103(10):104906.
12 Backhaus S,Tward E,Petach M.Travelling-wave thermoacoustic electric generator[J].Applied Physics Letters,2004,85(6):1085-1087.
13 Luo E C,Wu Z H,Dai W,et al.A 100W-class traveling-wave thermoacoustic electricity generator[J].Chinese Science Bulletin,2008,53(9):1453-1456.
14 Luo Ercang,Dai Wei,Wu Zhanghua,et al.Meso-Scope thermodynamic theory for cyclic flow engines,Part I:Meso-Scope thermodynamic model for cyclic flow regenerator[J].Cryogenics,2004(1):1-11.
15 Pfotenhauer J M,Shi J L,Nellis G F.A parametric optimization of a single stage regenerator using REGEN 3.2[J].Cryocoolers 13,Springer Science&Business Media,New York(2004):463-470.
