基于改进凸包算法的叶片型面特征参数提取

（华中科技大学数字制造装备与技术国家重点实验室，湖北 武 汉 430074）

叶片在航空航天、汽车、能源等领域，都有非常广泛的应用。据有关专家预测，到2025年，新增民用飞机（客机和货机）将达到2.72万架，全球机队规模将翻一番；到2020年，国内通用航空飞机将超过1万架。巨大的国际、国内市场，使得叶片的需求量迅速增大。

叶片型面一般为复杂曲面，加工工序比较复杂，其型面品质对发动机的性能起着决定性的影响[1]。如何检测和评估叶片的型面品质，已经成为航空制造领域的一个关键性技术问题之一。

目前，国内外主要采用人工卡板测量法和三坐标测量机（CMM）测量法，来对叶片型面进行检测。这两种方法都是离线式检测方法，检测速度比较慢。用激光扫描仪、结构光测量仪等非接触式测量设备进行叶片型面的检测，可以克服传统人工卡板测量法和CMM测量法的不足，并且实现叶片型面的在机检测，其还将成为叶片类复杂曲面型面精密检测的重要手段。利用非接触式测量得到叶片的点云数据，高效快速地提取叶片型面特征参数，具有重要的现实意义和实用价值。

如何根据测量得到的叶片数据，准确提取出叶片型截面凸包点云，是提取叶片型面特征参数的关键步骤之一。目前带有叶片检测模块的软件如Geomagic Qualify和Polyworks等均未提供叶片叶身轴线方向，叶片型面的截面选择具有任意性，从而使得提取的结果并不能真正体现叶片型面的特征。经典的凸包算法包括卷包裹（Jarris）法、格雷厄姆（Graham）方法以及分治算法等。这些算法在处理海量点云数据时，存在效率低下、精度难以保证等诸多问题。

刘人午提出先将数据点集进行一次扫描，得到横向和纵向排序点表并建立初始凸包，再运用增点法从外向内判别数据点是否加入凸包表的改进算法，成功解决了数据量超大时计算效率低下问题[2]。

但该算法存在两处不足之处：一是直接将大量的原始点集进行排序非常耗时，二是其判别算法结束的条件不具有通用性，从而使得到的结果不准确。

王文军提出以叶片截面在其最小外接圆上的各点之间距离最大者作为弦长[3]，由于没有在弦线上投影变换，使得计算结果不准确。

俞学兰在《基于MATLAB的叶片参数辨识》一文中详细讲解了求弦长的方法[4]，但该方法比较繁琐，且不能用于前后缘是椭圆型叶片弦长的计算中。

本文提出了基于主成份分析法的叶片叶身轴线方向的提取方法，并以此轴线方向为叶片型截面的法矢，准确截取叶片型面，得到叶片型截面点云数据。

本文改进了文献[2]的算法，用矩形区域腐蚀法确定凸包边界区域，删除矩形区域内的大量冗余点，大大提高了算法效率。

在叶片型面检测中，本文用改进的凸包算法来对测得的叶片型面点云数据进行排序，提取叶片型面关键特征参数。

在提取叶片前后缘参数时，传统的方法是按前后缘是圆弧的形式进行提取，但是近年来采用非圆弧形如椭圆形前缘可以明显改善叶片的气动性能[5]。

本文基于最小二乘法和随机原理，提出了一种用椭圆一般方程拟合叶片前后缘的抗噪声的高精度算法。最后，应用MATLAB软件开发了用于叶片型面特征参数提取的软件模块。

1 凸包算法的改进

凸包问题是计算几何的基本问题之一，在计算机图形学、图像处理、模式识别以及CAD、CAM等领域，都有着广泛的应用[6]。

构建凸包通常要解决两个问题：其一是要从大量的离散点中判断出哪些是符合要求的凸包顶点；其二是要解决这些点的拓扑连接关系。

文献[2]求取凸包最耗时的地方，是对点集快速排序与生成凸包。如果能够减少参与排序和生成凸包的点集数量n，就可大大提高算法的效率，本文基于该思想，提出用矩形区域腐蚀法确定凸包边界区域，以删除矩形区域内的冗余点。

1.1 针对文献[2]算法做出的改进

本文根据凸多边形的边同侧特性[7]，针对文献[2]的算法做出如下改进：

（1）用矩形区域腐蚀法确定凸包边界区域，删除矩形区域内大量的冗余点，形成初始的平面点集；

（2）找出初始平面点集中的极值点构成初始凸包；

（3）将初始平面点集中的点进行扫描得到按x、y坐标值从小到大排序的横向排序表H（x值相同，按y值从小到大排序）和纵向排序表V（y值相同，按x值从小到大排序）；

（4）在每次调入H、V点集中第一点和最后一点进行判别后，要重新生成H、V点集，并判断这两个点集是否为空，若全为空时，结束判断，生成凸包点集。

矩形区域腐蚀法原理如下：

先找出点集中的4个边角点，即

A点（x+y值最小的点），

B点（x–y值最大的点），

C点（x+y值最大的点），

D点（y–x值最大的点）

然后用

y ＝ max（Ay，By），

y ＝ min（Cy，Dy），

x ＝ max（Ax，Dx），

x ＝ min（Bx，Cx）

画直线围成矩形区域，最后用腐蚀法将点集中落于这个矩形区域的点腐蚀掉，剩下凸包边界区域点，即初始平面点集，如图1所示。

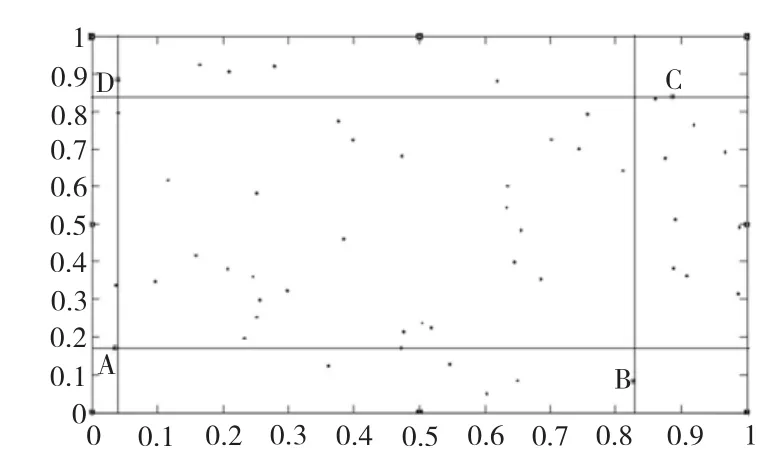
图1 矩形区域腐蚀法示意图

1.2 初始凸包生成方法

（1）找出点集中的极值点。

A1为x坐标等于x min的点中y坐标最小的点；

A2为x坐标等于x min的点中y坐标最大的点；

A3为y坐标等于y max的点中x坐标最小的点；

A4为y坐标等于y max的点中x坐标最大的点；

A5为x坐标等于x max的点中y坐标最大的点；

A6为x坐标等于x max的点中y坐标最小的点；

A7为y坐标等于y min的点中x坐标最大的点；

A8为y坐标等于y min的点中x坐标最小的点。

（2）将这些极值点按顺时针方向的顺序，写入数组A中，即

A＝[A1；A2；A3；A4；A5；A6；A7；A8]

(A为8×2的数组)。

（3）删除A中相同的点并将A中的第一点复制增加为A的最后一点，使其首尾相连，形成初始凸包如图2所示。

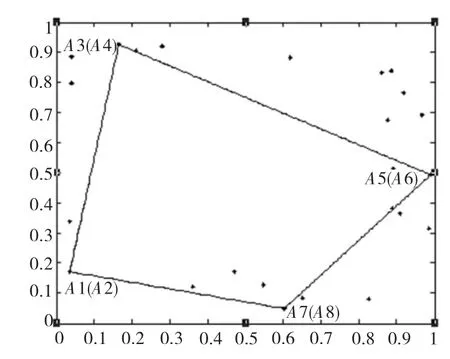
图2 初始凸包生成示意图

1.3 定义点与有向直线的关系判别函数

定义点与有向直线的关系判别函数S如下：设

A(xa、ya)、B(xb、yb)和 C(xc、yc)

为XY平面内任意不同的3点，记

L（AB）为A指向B的有向直线，用三点面积S判断点C与L(AB)的侧向关系，其判别函数为

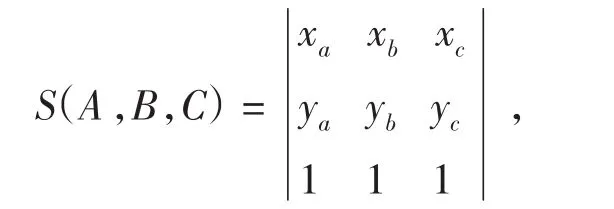
S为正时，表示A、B、C是逆时针；

S为负时，表示A、B、C是顺时针。

（1）如果 S＞0，点 C 在 L（AB）的左侧；

（2）如果S＝0，点C在L(AB)上；

（3）如果S＜0，点C在L(AB)的右侧。

如果当前判断点在当前凸包外(存在一条边使得该点在该边的左边)，则将该点插入凸包表中该边的两端点之间[2]。这种说法欠妥，如果这个点在当前凸包相邻两边交点的外顶点区域，增加到其中任一边两端点之间后，会使凸包发生畸变，改变了这个多边形的凸包属性。

改进如下：

设凸包两相邻边为AB、BD，当前判断点C，

若 S（A，B，C）＞0

且S（B，D，C）≤0，C点增加到边AB 两端点之间；

若 S（A，B，C）＞0

且 S（B，D，C）＞0，去掉 B 点，C 点增加到边 AD两端点之间。

1.4 凸包算法流程及其效率分析

凸包算法流程如图3。

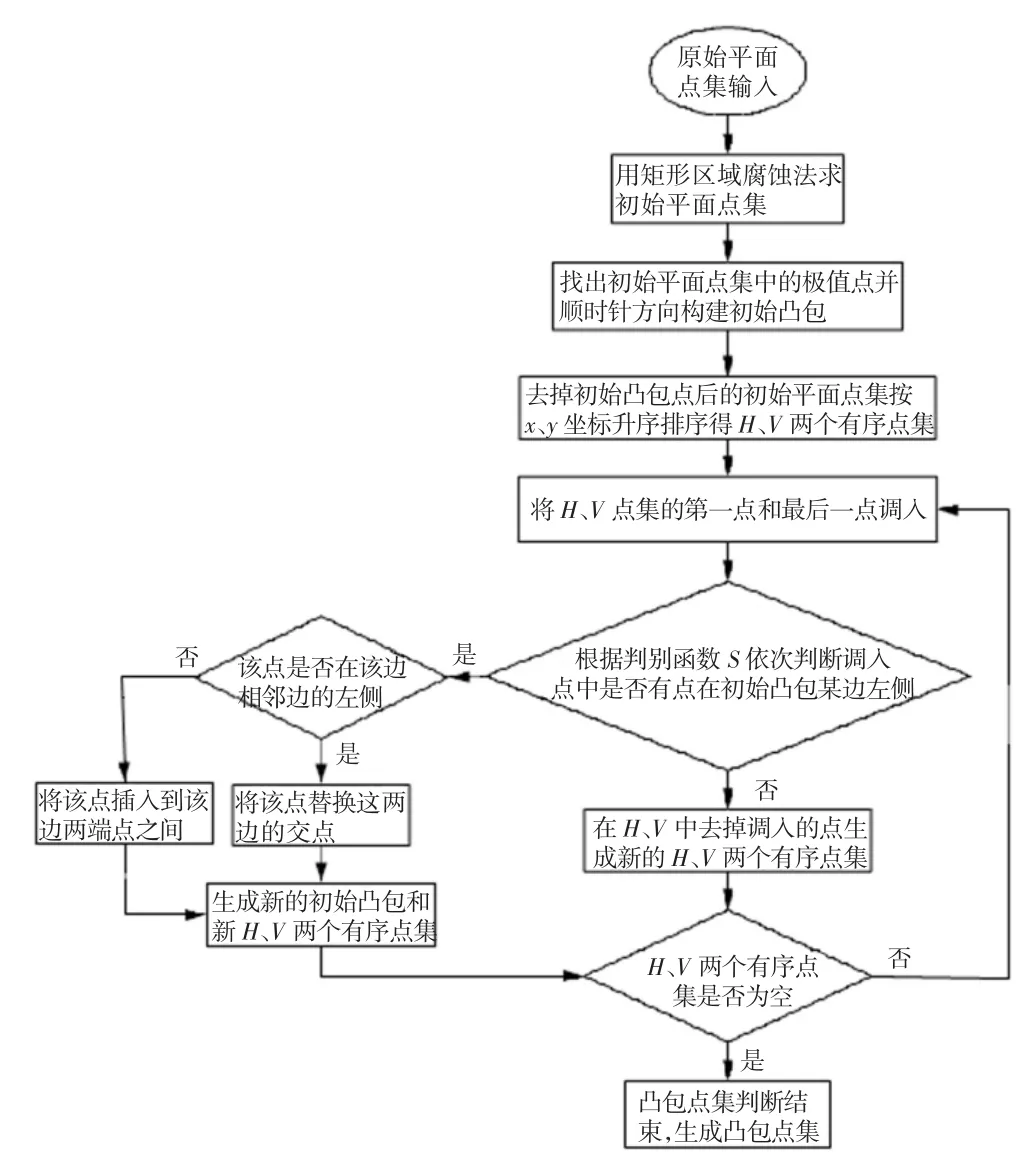
图3 凸包算法流程图

下面进行该算法效率的分析：

该算法主要分4步：

第一步是用矩形区域腐蚀法求原始平面点集（设点数为n）得初始平面点集（设点数为n1），n1大约是n的1/10，其时间复杂度为O（n）；

第二步是提取初始平面点集中的极值点生成初始凸包，其时间复杂度为O（n1）；

第三步是对去除初始凸包点后的初始平面点集（设点数为n2）进行双向排序生成H、V集，若采用时间复杂度逼近于O（n）的排序方法时[8]，其时间排序的时间 O（n2）；

第四步根据判别函数S，在初始平面点集中提取凸包点生成凸包，其时间复杂度为O（n2）。

综合起来，该算法的时间复杂度为O（n），这与目前平面点集凸包问题的渐进最好算法的时间复杂度为O（n log h）相比，下降了一个数量级，具有很好的时间效率[9]。

在2G内存2.5 GHz主频的电脑上，利用MATLAB软件编程对上述算法进行实验分析。

在用矩形区域腐蚀法删除矩形区域内部点效率分析的实验中，点集的坐标由随机函数（rand）产生，在实验中分别设置点集数量为103、104、105、106、1.5×106和1.5×107，实验结果如表1所示。实验表明，大约有90%以上的冗余点集，可以通过本算法删除。

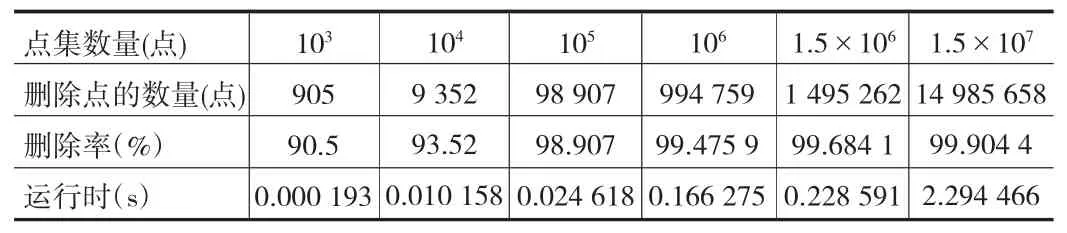
表1 用矩形区域腐蚀法删除矩形区域内部点效率分析

在凸包算法运行结果比较实验中，点集的坐标由随机函数（rand）产生，文献[2]和本文的算法运行结果如表2，可以看出本文算法所费时间比文献[2]少一个数量级，原因在于本文在进行初始平面点集排序前运行矩形区域腐蚀法去除了矩形区域内的大量冗余点，使其点数锐减为原来点数的3‰左右，从而大大提高了程序的运行效率。

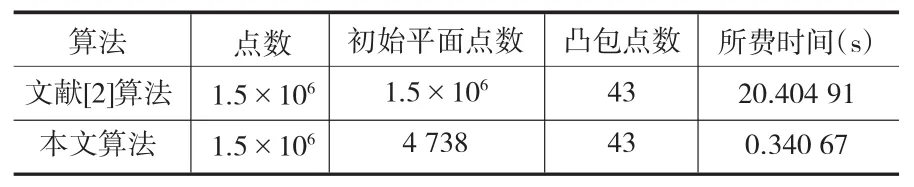
表2 凸包算法运行结果

2 叶片型截面凸包点云数据的提取

为了体现出叶片型面特征，不能随意用一个平面去截取叶片型面，必须使截平面垂直于叶片叶身的轴线，即截面的法矢与轴线方向一致，以确保准确提取出叶片型面的特征参数。

在接触式测量中，可以精确调整坐标轴，使其Z轴与叶片叶身轴线一致（如图4），这样在测量的叶片点云数据中锁定Z轴，根据具体的精度要求，以一定的间隔△Z移动垂直于Z轴的截面去截叶片型面，即可得相应的叶片型截面点云数据（如图5)。

图4 CMM测量叶片

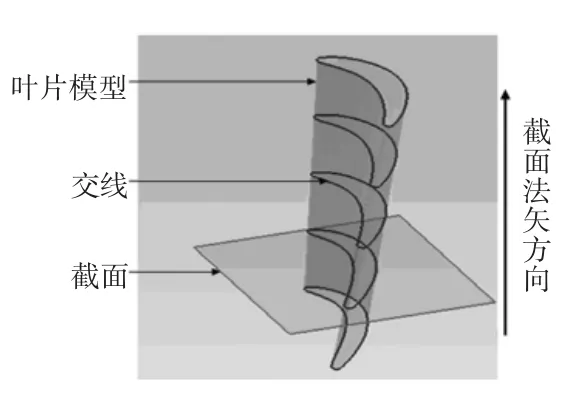
图5 叶片截面示意图

在非接触式测量中，由于测量仪坐标轴方向随机，叶片叶身轴线与坐标轴不一致，我们可以通过对测量的叶片点云数据进行主成份分析找到叶片叶身的轴线方向[10]，并将叶片点云数据通过坐标转换，使其新坐标系的Z新与叶片叶身轴向一致，然后根据精度要求以一定的间隔△Z新移动垂直于Z新轴的截面去截叶片型面得到相应的叶片型截面点云数据。下面介绍一下基于主成份分析法提取叶片叶身轴向的方法。

主成份分析法是一种降维的统计方法（Principal Components Analysis，PCA），也是一种数学变换的方法，其借助于一个正交变换，将其分量相关的原随机向量，转化成分量不相关的新随机向量，这在代数上，表现为将原随机向量的协方差矩阵变换成对角形阵；在几何上，表现为将原坐标系变换成新的正交坐标系。

经过特征矢量矩阵的转置矩阵作为变换矩阵变换后，新的坐标轴是沿数据分布的主要分量方向即特征矢量的方向。对于二维空间，如果数据分布是一椭圆，那么特征矢量正好在椭圆的两个轴上，U轴方向是第一主成份，V轴是第二主成份方向，如图6所示。

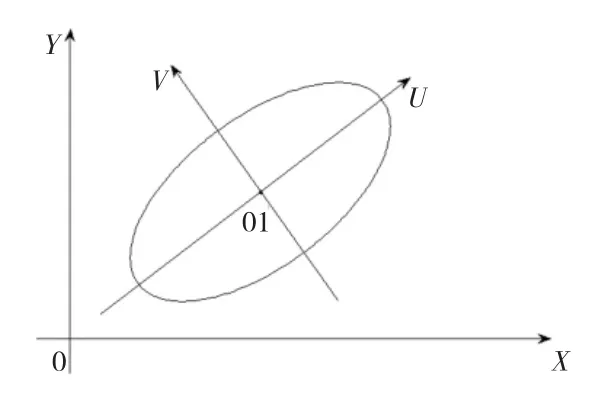
图6 椭圆主成份分析示意图

这样，将原相关变量集在特征向量空间的投影，即得不相关变量集，其特征向量矩阵为投影变换矩阵，也为XOY坐标系到UO1V坐标系的变换矩阵。

利用主成份分析法提取叶片叶身轴向的一般步骤为：

（1）根据叶片点云数据

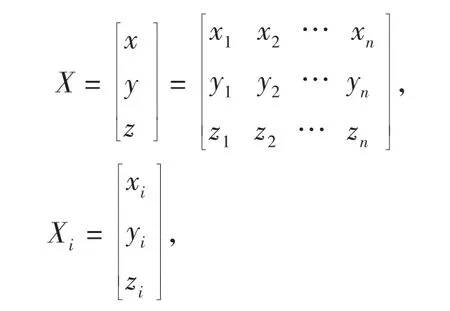
计算其数学期望

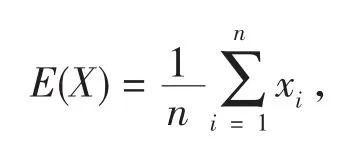
协方差矩阵

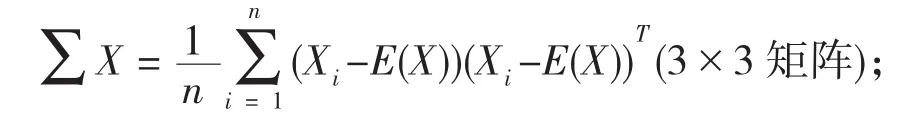
（2）对协方差矩阵ΣX用特征值分解。即

ΣX× V=V×D，

D为ΣX的特征值对角阵；

V为ΣX的特征向量矩阵；

从而计算变换矩阵A=VT和主成份矢量方向。

根据叶片叶身长度与叶片型截面的长宽粗略比较：

若叶身长度是最长的，则选第一主成份（特征值最大）矢量方向为叶身轴向；

若为第二长，则选第二主成份（特征值第二大）矢量方向为叶身轴向；

若为第三长，则选第三主成份（特征值最小）矢量方向为叶身轴向。

（3）用A×X即得叶片点云数据在新坐标系下的点云数据X新。

在MATLAB中，改进的凸包算法，能高效处理测得的叶片点云数据：获取按逆时针排序的叶片型截面凸包点云数据；将余下的凹点按x坐标值的升序排列求得叶片凹弧点云数据。这样就将叶片型截面点云数据就按逆时针有序排列了（见图7），为后面的叶片型截面数据处理作好了准备。

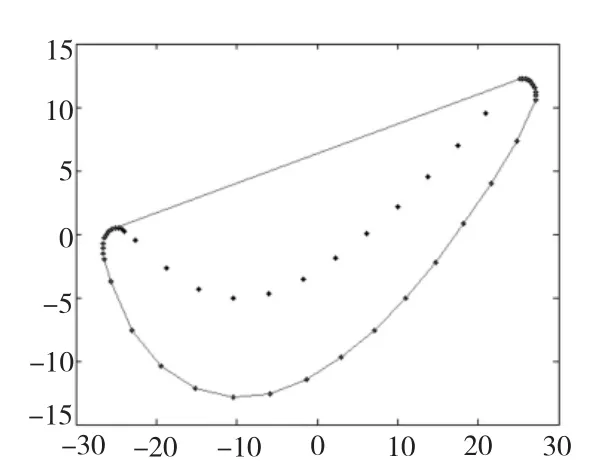
图7 叶片型面凸包点云数据

3 叶片型面特征参数的提取

叶片的型面检测通过型面特征参数来表达,这些参数主要包括弦长及弦倾角、前后缘点、中心、半径及厚度、型面最大厚度、中弧线等，具体定义如下（图8所示）。

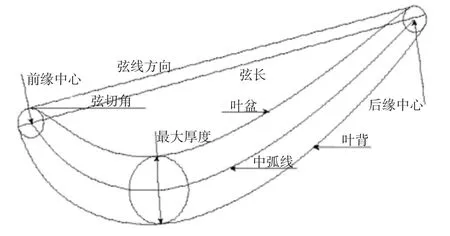
图8 叶片型面特征参数示意图

弦线：叶片型截面上与叶盆的前后部型线同时相切的切线。

弦长：整个叶片截面轮廓在弦线上投影的长度。

轴弦：整个叶片截面轮廓在发动机轴心线上投影的长度。

弦倾角：弦线与发动机轴心线的夹角即为弦倾角。

前后缘点：分别是中弧线延拓后与前缘曲线和后缘曲线的交点。

前后缘中心：前后缘拟合后图形的几何中心，若前后缘是圆形则为圆心。

前后缘半径：对于圆弧形缘头，即为缘头所在圆的半径；其他类型的缘头不存在此参数，如椭圆就是长短轴。

前后缘厚度：叶片型面中弧线上距离前后缘点1 mm处点为圆心的叶型内切圆直径。

中弧线：由一系列叶身截面内切圆圆心定义的曲线。

最大厚度：一系列叶身截面内切圆中的最大内切圆的直径。

限于篇幅，本文仅对叶片型面弦线及前后缘关键特征参数提取算法进行详细介绍，对其他叶片型面关键特征参数，根据其定义在MATLAB中也可方便求解。

3.1 弦线及其参数提取

弦线为叶片型截面上与叶盆的前后部型线同时相切的切线。弦线提取技术的关键，是获取弦线与叶盆前、后缘相切的切点。根据前面提取的叶片型截面凸包数据特点，可以认为凹线的两端点即叶盆与叶背的交点为待求的两切点。弦线提取方法如下：

（1）采用凸包算法获取轮廓数据点的凸包；

（2）逐个计算凸包中相邻两点的距离，获取距离最大的相邻两点；

（3）过该两点作直线，即为弦线，该弦线斜率的反正切值，就是弦线与X轴（设X轴方向为发动机轴心线）的夹角，即弦倾角。

弦长为整个叶片截面轮廓在弦线上投影的长度。对于前后缘不是圆形，是其他图形如椭圆，采用俞学兰法会过于复杂，因此研究一种通用的计算弦线参数的方法具有重要意义。

根据弦长的定义，弦长的计算可以将测得的点云数据往弦线方向投影，求其在新坐标系下的坐标，然后求在新坐标系X坐标最大的点与X坐标最小的点的距离即为弦长（简称投影变换法）。投影变换法的原理如下：

假设弦线L通过平移与X轴交于原点O，夹角为弦切角α。通过绕Z轴逆时针旋转α，使X轴与弦线L重合如图9所示。

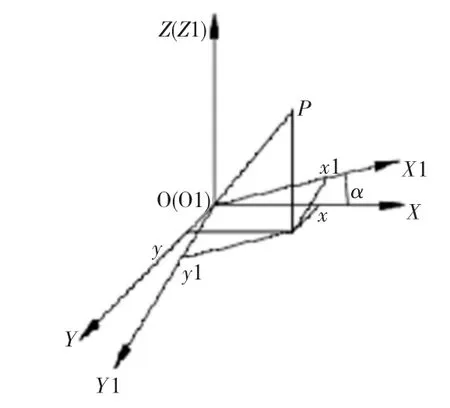
图9 坐标转换示意图

同一点P在原坐标系OXY下的坐标为P0（x，y），在新坐标系O1X1Y1的坐标为P1（x1，y1），则P0和P1具有如下变换关系：

弦长 L＝max（P1x）– min（P1x）

(即叶片点云数据转化到新坐标系后的x坐标最大值与x坐标最小值之差)。

几种方法计算弦线参数结果如表3所示，由表可知，本文提出的投影变换法计算弦线参数可靠，且能通用于任意形状的叶片截面。

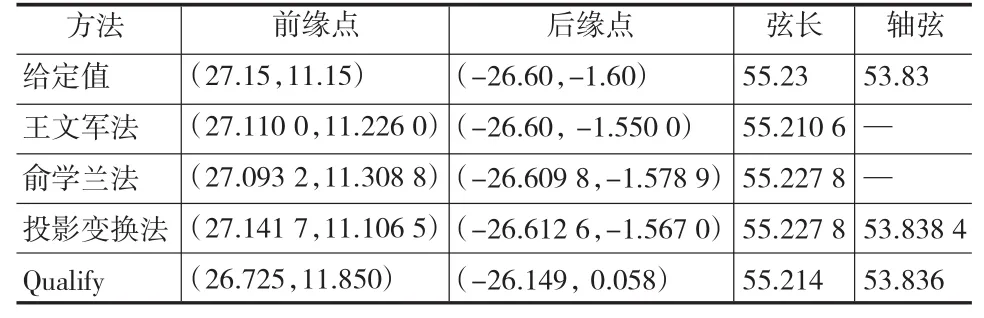
表3 几种方法弦线参数计算结果 单位：mm

3.2 前后缘参数提取及叶片型面精确分割

由于圆是椭圆的特殊情况，所以可以直接设叶片前后缘类型为椭圆弧，根据椭圆的一般方程建立模型

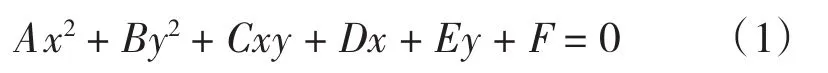
（如果A＝B则为圆；如果A≠B则为椭圆）。

基于代数距离最小二乘法的常规椭圆拟合法将所有样本点都当作准确值来拟合[11~13]，但当样本点中出现杂质点时，拟合出的椭圆误差较大，不能满足精确度要求较高的系统需求，因此在拟合前后缘参数前，要精确提取出前后缘上的点。

（1）粗略确定前后缘的范围。在前面提取凸包后，将弦线两端点沿前后缘方向上取相对精确的6个点，代入方程（1）得到拟合椭圆的相关参数，计算叶片型截面点云数据到这个椭圆方程的欧式距离d，若d≤△d（设定的阀值），则认为该点在椭圆上，从而得到叶片前后缘的粗略范围（记为样本点云）。

（2）精确确定前后缘上的点云数据。在第一步求取的前后缘点中，有可能含有噪声，如何除去前后缘上的噪声，即不在椭圆上的点，本文基于最小二乘法和随机原理，提出了一种能有效去除前后缘噪声确定前后缘精确数据点的方法。

其算法原理如下：

其一，在初步确定的前后缘范围内的样本点云（已编号）随机取6个点。

其二，将这6个点代入

Ax2+By2+Cxy+Dx+Ey+F=0中，

求得 A、B、C、D、E、F。

其三，计算样本点云中所有点到前面6个点拟合成的椭圆的代数距离，即

D＝｜Ax2+By2+Cxy+Dx+Ey+F｜。

若D≤△D（设定的阀值），将这个点的编号记入数组Dianhao中，然后将样本点云中满足要求的点的总个数记入Dianshu中。

其四，比较匹配点总个数（Dianshu）与匹配点数最大值（Maxdianshu），当前者大于后者，将椭圆参数(A、B、C、D、E、F)和记录匹配点编号的数组（Dianhao）保存下来,分别拷贝至数组Canshu和数组Maxdianhao，最后将Dianshu赋值给Maxdianshu。

其五，循环执行步骤其一到其四一定次数（根据运行时间、需要结果的准确度以及样本点总个数适当定义），最后在Canshu保存了最优椭圆参数，在数组Maxdianhao保存了在所有样本点中匹配点的编号，也就可以相应地得到不匹配点的编号。

算法流程图如图10所示。根据Maxdianhao中保存所有样本点匹配的编号，求得前后缘精确的点。

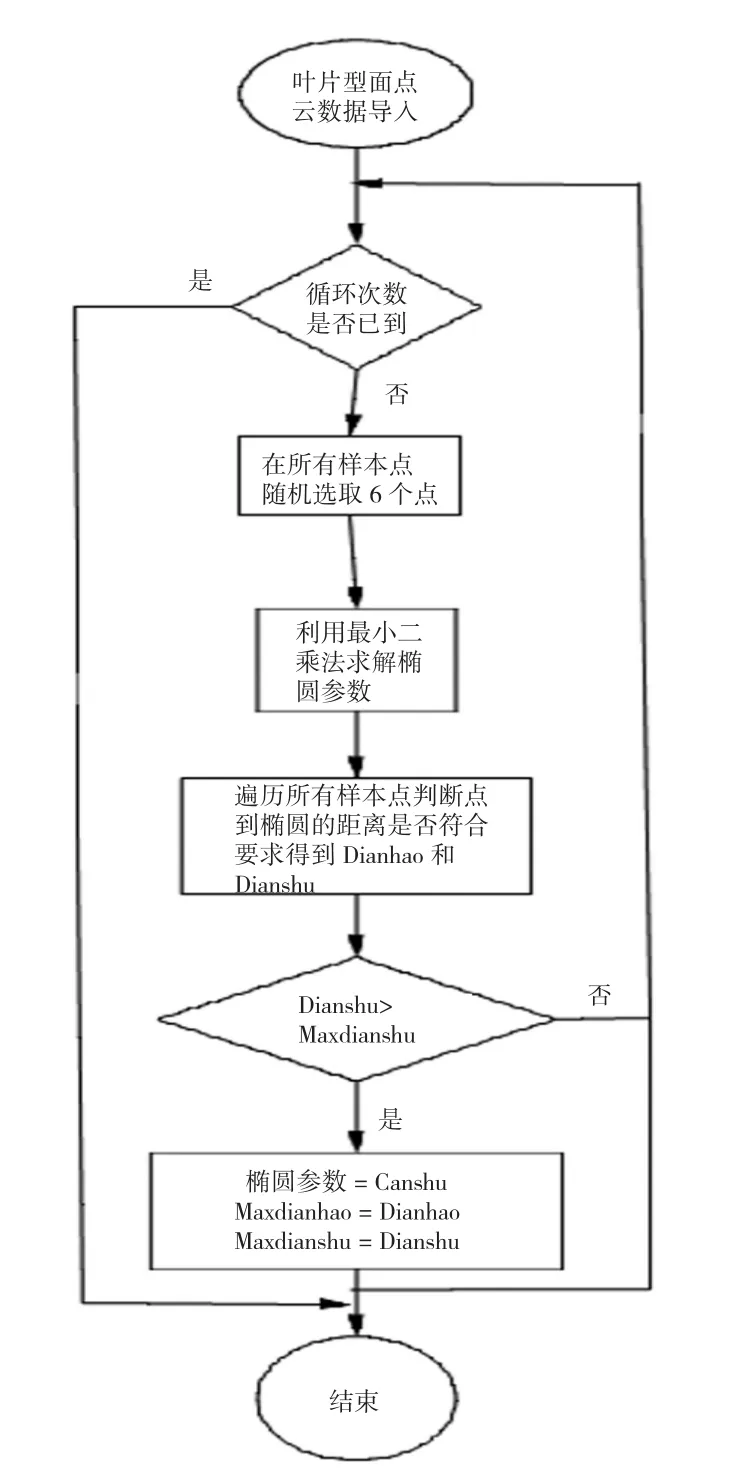
图10 前后缘参数算法流程图

算法实验：将方程为(x2)/9+(y2)/25＝1的椭圆离散成63个点，设定循环次数为N次，D的阀值为△D，在不同的高斯噪声（0，σ2）下，本算法提取到符合要求的点数为n1，椭圆的5个参数及运行时间。

在不同的噪声（即改变σ2）下，拟合结果如表4、表5所示，从表可以看出在N＝200，△D＝0.001情况下，除噪声效果最好。

经过实践证明，在求取最优椭圆的过程中，剔除了绝大多数的杂质点，相比传统方法，准确度得到一定提高，系统鲁棒性得到增强，且所需运行时间较短。

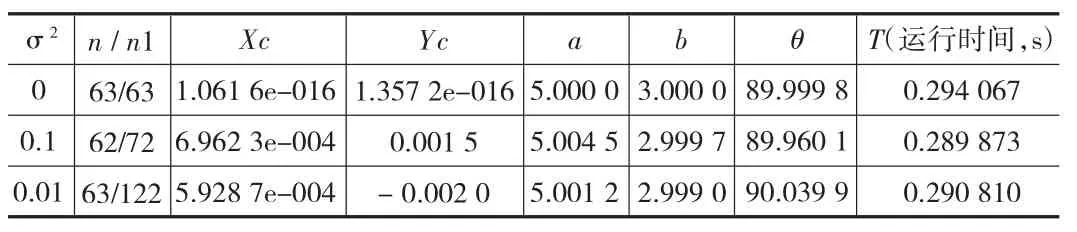
表4 本文方法对含有噪声数据的拟合结果(N=100,△D=0.01)

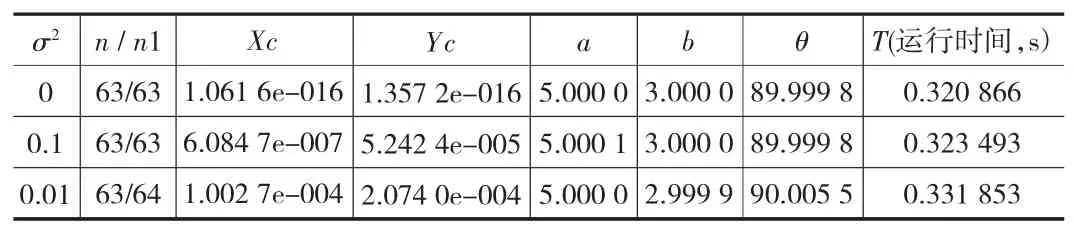
表5 本文方法对含有噪声数据的拟合结果（N＝200，△D＝0.001）

（3）精确确定前后缘的参数。在确定前后缘数据点后运用椭圆拟合的程序确定前后缘的精确参数，若椭圆的长短轴相差的绝对值不大于error(设定的阀值)，再运用圆拟合程序进行拟合得到圆弧形前（后）缘的精确参数（提取前后缘结果如图11）。

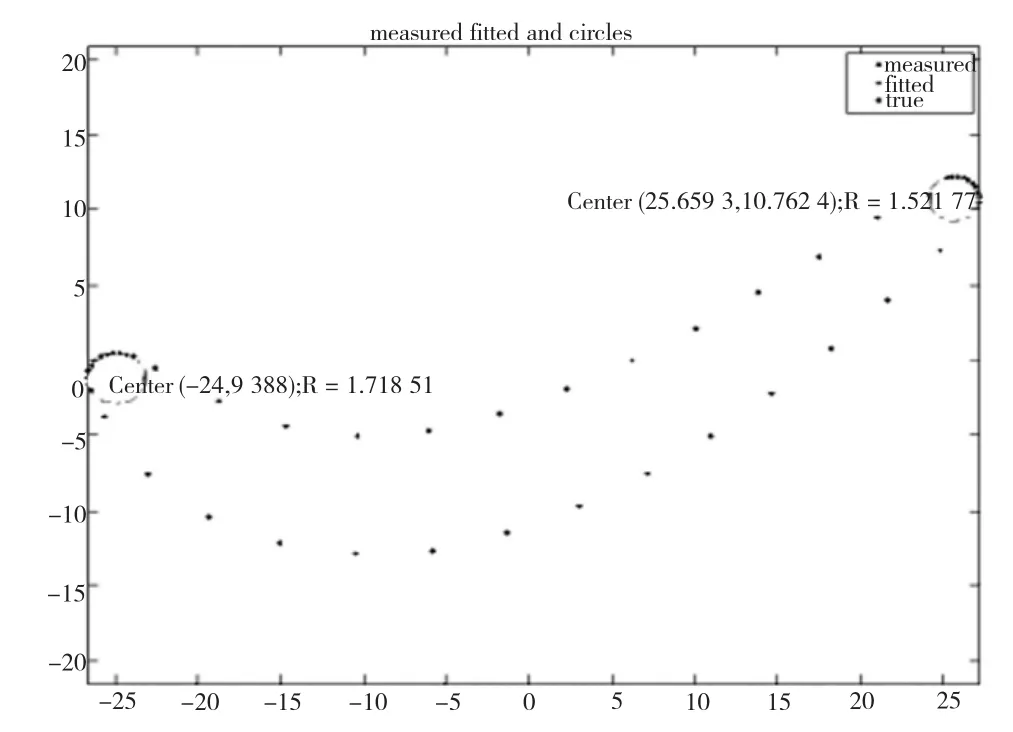
图11 叶片截面前后缘提取结果

（4）叶片型截面点云的精确分割。叶片型截面点云数据可分为如下4部分：叶盆、叶背、前缘、后缘。在精确确定前后缘点后，凸包上的点集减去在其上的前后缘点即得叶背部分点云，凹弧部分的点集减去在其上的前后缘点即得叶盆部分点云。

4 叶片型面特征参数提取的GUI设计

在研究叶片型面关键特征参数提取算法的基础上，利用MATLAB软件的GUI模块，编写了一个提取叶片型面特征参数的用户界面，便于实现人机交互。

该界面主要包括叶片型面测量点云的输入（*.dat或*.txt格式）、图形显示设置（如线型、线宽、网格、坐标轴等）、处理后结果的显示（如文本输出、各特征参数在图形窗口中的显示等）。

将某型号航空发动机叶片型面的激光扫描点云数据，导入到叶片型面特征参数提取的软件模块，提取结果如图12所示。

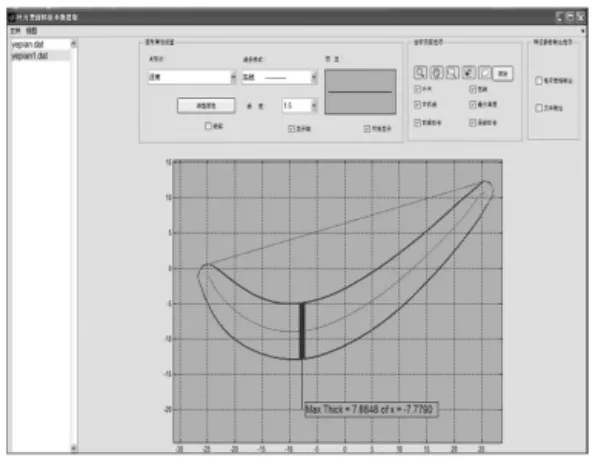
图12 叶片截面特征参数提取界面

本文方法提取的结果与Geomagic Qualify软件提取结果（如图13）的比较见表6。本文采用了时间效率高的凸包算法，并改进了叶片型面特征参数的提取算法，从表6给出的数据可以看出，本方法在精度上比这款软件高。

另外，本方法在提取叶片型面特征参数方面比Qualify软件有更好的操作性。

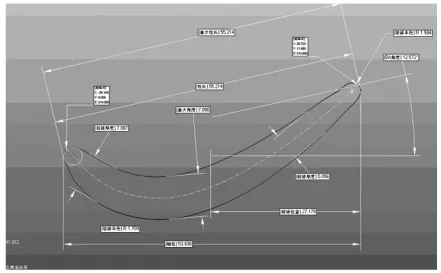
图13 Qualify软件提取叶片型面参数结果

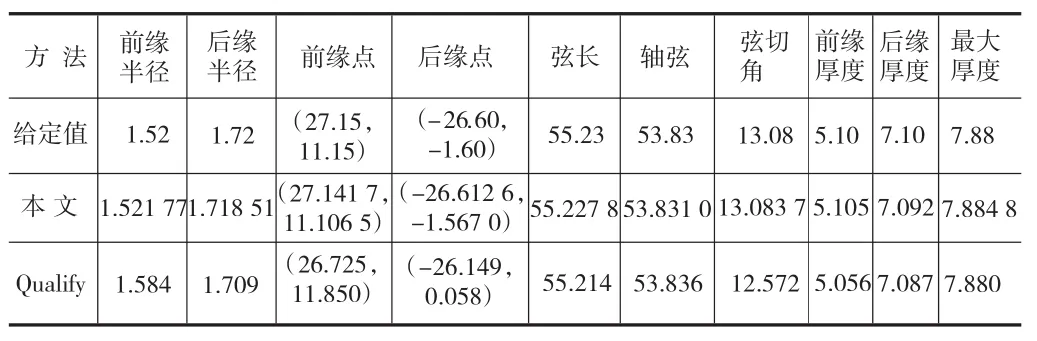
表6 叶片截面特征参数提取结果比较

5 结束语

本文提出了基于矩形区域腐蚀法的改进凸包算法，用于提取叶片型面特征参数，如弦线、前后缘参数等，实验结果表明，改进后的算法具有更高的计算效率和计算精度，通用性好，且具有一定的抗噪能力。主成份分析法用于分析和提取叶片截平面法矢，为准确提取叶片型面特征参数提供方向矢量。在Matlab软件平台下开发了面向叶片测量点云数据叶片型面特征参数提取的人机交互界面，并通过实验数据验证了该软件模块的可行性与有效性，为航空发动机叶片在机非接触式检测应用提供了基础。

[1]陆佳艳，熊昌友，何小妹，等.航空发动机叶片型面测量方法评述[J].计测技术，2009，29(3)：1-3.

[2]刘人午，杨德宏，李 燕，等.一种改进的最小凸包生成算法[J].大地测量与地球动力学，2011，31(3)：130-133.

[3]王文军.基于Surfacer叶片型面检测模块的开发[D].无锡:江南大学,2008.

[4]俞学兰，叶佩青.基于MATLAB的叶片参数辨识[J].航空维修与工程，2009，(4)：56-58.

[5]张力宁，张定华.叶片前缘高精度重建方法研究[J].航空动力学报，2006，21(4)：722-726.

[6]李光军，郑军红，张光忠.一种凸包的改进算法设计与实现[J].现代计算机(专业版)，2010，(6)：92-94.

[7]刘光惠，陈传波.求解简单多边形和平面点集凸包的新算法[J].计算机科学，2007，34(12)：222-226.

[8]Pigeon S.Quicksort and radix sorts on lists[J].Dr.Dobb's Journal，2002，27(5)：89-89.

[9]Kirkpatrick D G,Seidel R.Ultimate planar convex hull algorithm[J].SIAM Journal on Computing，1986，15(1)：287-299.

[10]白困利.基于主成份分析法的绝缘子外绝缘特性的综合评判[J].华中电力，2010，23(2)：9-12.

[11]Fitzgibbon A，Pilu M，Fisher R B.Direct least square fitting of ellipses[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1999，21(5)：476-480.

[12]雷志术，张雁波.椭圆定形曲线拟合问题若干新型算法[J].上海交通大学学报，2002，36(8)：1210-1213.

[13]Halí R，Flusser J.Numerically stable direct least squares fitting of ellipses[C].The sixth International Conference in Central Europe on Computer Graphics and Visualization[A].1998，1(1)：125-132.