基于柔性多体动力学的混凝土泵车臂架仿真分析

（长沙理工大学汽车与机械工程学院，湖南 长沙 410114）

混凝土泵车，是把泵送混凝土的泵送机构和用于布料的臂架系统，集成在汽车底盘上的专用车辆。作业时，利用底盘发动机的动力，通过分动箱将动力传给液压泵，然后带动混凝土泵送机构和臂架系统，泵送系统将料斗内的混凝土加压送入输送管道内，输送管安装在臂架上，臂架系统可大范围移动，从而将混凝土直接送到浇注点。

臂架系统用于完成混凝土的输送和布料作业。通过转台旋转、油缸伸缩，将混凝土送达臂架末端软管所指位置，完成浇注。臂架系统由臂架、连杆、连接件和油缸等部件组成，具有足够的强度、刚度的同时，保证自身净质量小，是泵车臂架系统设计的基本要求。在实际作业中，混凝土泵的两个油缸交替循环动作，将对整个臂架系统产生冲击作用，从而引起臂架振动，最终影响泵车的使用寿命和混凝土浇注精度。

本文采用三维建模、有限元分析和多体动力学仿真，建立包括臂架柔性体以及其他零部件刚性体在内的整个臂架系统的虚拟样机模型，对臂架系统进行动态分析，更加精确地得到了臂架系统在真实工况下工作的的实时动力学响应分析。

1 臂架系统的动力学模型分析

1.1 受力分析

泵车结构采用高强度进口钢；

定义材料弹性模量为2.1×105MPa；

泊松比为0.3；

密度为7 850 kg/m3。

鉴于动态负荷的影响，还应在臂架系统自重载荷的数值上乘以系数1.2[1]，在ADAMS软件中开启重力选项，系统仿真时会根据各结构密度自动处理各部件的重力。为模拟输送管中充满混凝土时的真实效果，将输送管和混凝土两种材料的等效密度产生的重力加载在输送管上，混凝土的密度规定为2.4 t/m3，计算方法为

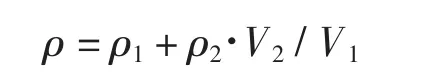
ρ、ρ1、ρ2分别为输送管和混凝土的等效密度、输送管密度、混凝土密度；

V1、V2分别为单位长度输送管体积、单位长度混凝土体积。

将输送管输送混凝土产生受到的摩擦力，加载在各节臂架的托架上，末端软管及其中混凝土的重力，以力的形式作用在第5节臂末端点[2]。混凝土泵的周期性推动力，模拟成一个谐波函数力加载到转台上。根据混凝土泵车标准QC/T718—2004，布料杆在有风的情况下工作时，风载荷是一个沿任意方向的水平力，计算风压力为25 N 0/m2。

1.2 臂架系统动力学模型参数

该臂架系统模型在三维软件UG中建立，将模型存为Parasolid格式导入ADAMS中，修改模型的外观和名称。单位设置为MMKS（长度mm、质量kg、力N、时间s、频率Hz）。开启重力项，通过定义材料密度等到各结构质量。添加系统约束副，创建固定副、旋转副和圆柱副，添加驱动。构件之间同轴旋转时用旋转副约束，油缸和活塞用圆柱副约束，转台和大地之间用固定副约束，各节输送管和各节臂架也用固定副约束[3]。臂架系统模型如图1所示。

图1 臂架系统三维模型

2 刚柔混合模型的建立

混凝土泵车臂架系统，具有连续分布的质量，而连续体具有无限多个自由度。利用有限元法，将无限多个自由度系统离散成有限多个自由度系统，所以问题可描述为柔性体任意单元上任意节点的形位。在多体系统中，用非线性代数约束方程，描述各构件之间的连接点和指定轨迹，表示为

C(q，t)=0

式中，

q为柔性体的广义坐标；

t为时间。

将柔性体的动能、应变能、广义力虚功和约束方程式通过拉格朗日乘子引入，得到物体的柔性多体系统运动方程

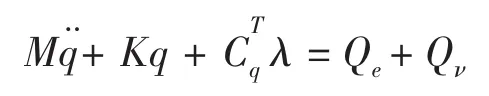
式中，

M为柔性体质量矩阵；

K为刚度矩阵；

q为节点位移；

λ为拉格朗日乘子；

Qe为整体载荷向量；

Cq为约束雅可比矩阵；

Qν为动能对时间和物体坐标取导得到的二次速度矢量，包括回转力和哥氏力分量。

将以上两式联立，得到柔性多体系统动力学模型：

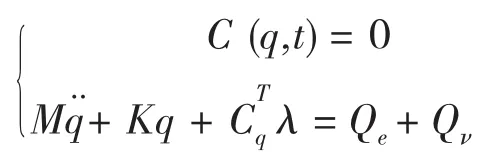
解之，得物体任意点在运动过程中各时刻的位置、速度和加速度，进一步得到各时刻系统的应力和应变，获得瞬时动态响应。

根据多体系统动力学理论，在混凝土泵车实际工作时，臂架系统的运动为大范围的臂架系统运动，与臂架弹性变形的耦合，将整个臂架系统完全作为刚体来分析，而得到的结果达不到精度要求，所以有必要把臂架作为可以产生变形的柔性体来处理。考虑到计算机仿真速度，把油缸、转台和连杆仍作为刚形体处理。臂架柔性化而其他构件刚性的模型为刚柔混合模型。

通过有限元分析软件ANSYS将5节臂架柔性化处理。首先将各节臂架模型导入到ANSYS中，通过划分网格将臂架离散成细小的网格。对于需要建立关联运动副的位置，要设置节点，并且将此节点指定为外连节点，可以通过各个节点在ADAMS中创建运动副和载荷的受力点[4]。

臂架受力不是作用于某一点，而是作用在孔臂区域上，所以可以将外连节点与周围相邻区域的节点固化。以一节臂为例，共需要建立9个外连节点，其中5个外连节点建立在臂架旋转副处，其他4个建立在臂架与混凝土输送管连接处。一节臂架外连点固化图如图2所示。

图2 第一节臂架外连点固化图

由于臂架振动起主导作用的是低阶固有频率，而高阶固有频率对臂架的振动影响小，所以进行模态计算时取前10阶模态，一节臂架上有9个外连节点，最终得到模态数共有

9×6+10=64阶。

在做自由模态计算时，臂架前6阶为刚性模态，频率值近似为0 Hz，一节臂前7阶柔性模态固有频率值及振型描述见表3，前12阶模态振型见图3。

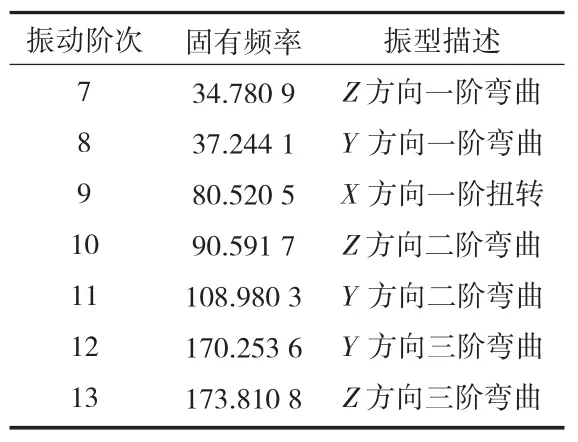
表3 一节臂固有频率和振型描述

图3 一节臂前7阶柔性模态振型

将计算的模态保存为模态中性文件（MNF文件），然后再用柔性臂架替代原来的刚性臂架，得到臂架系统的刚柔混合模型。

图4 第一节臂的刚柔混合模型图

3 刚柔混合模型的动力学仿真

生成臂架系统刚柔混合模型后，对臂架系统在最危险工况5节臂水平外伸工况下，做某施工动作的动力学仿真。设定油缸1的活塞在20 s内匀速伸出0.8 m，油缸2、油缸4和油缸5的活塞在10 s内匀速缩回0.1 m，油缸3的活塞在10 s内匀速缩回0.2 m。

为定义各节臂架系统的动作，在各液压缸的移动副上加一个关于时间的STEP函数，各个液压缸的驱动函数分别为

N1=STEP(time，0，0，20，800)；

N2=STEP(time，20，0，30，100)；

N3=STEP(time，30，0，40，200)；

N4=STEP(time，40，0，50，100)；

N5=STEP(time，50，0，60，100)。

在上述仿真条件下，用ADAMS对臂架系统进行系统动力学分析。

图5 臂架系统末端轨迹

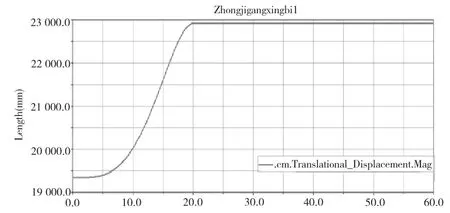
图6 臂架1质心刚体仿真位移时间曲线

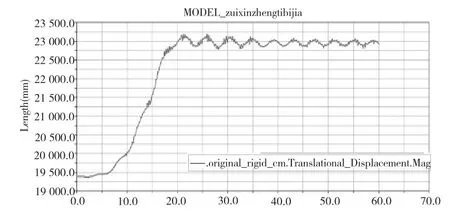
图7 臂架1质心柔体仿真位移时间曲线

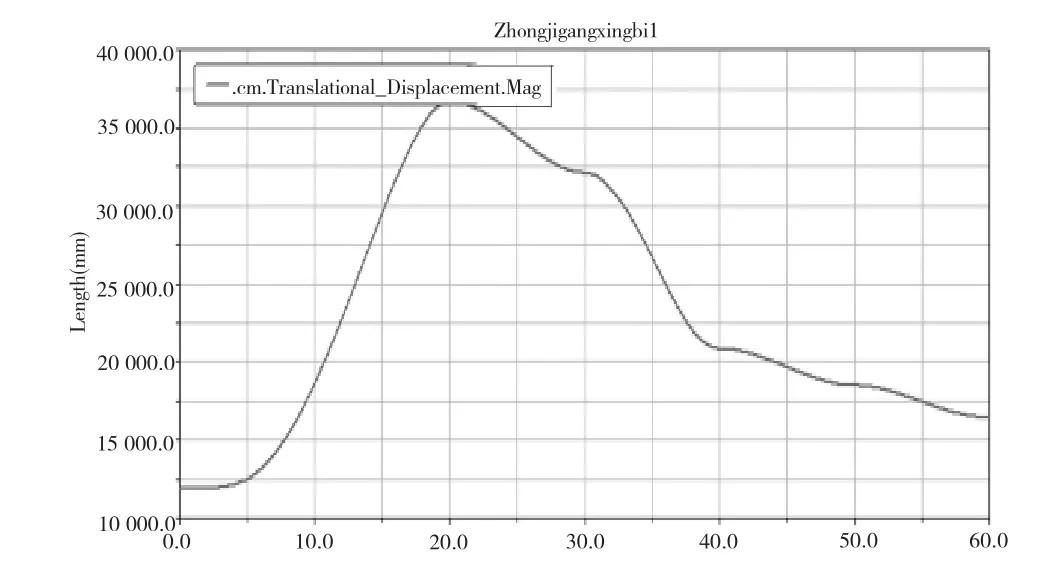
图8 臂架5质心刚体仿真位移时间曲线

图9 臂架5质心柔体仿真位移时间曲线

4 结果分析

综合比较图7～图10，可以发现，刚性臂架系统与刚柔混合模型臂架系统的仿真，有明显不同。图7与图9为纯刚体仿真，运动过程不存在振动，曲线变化较为平缓；图8与图10为刚柔混合体仿真，运动时臂架发生了抖动，仿真曲线波动，这是因为考虑了臂架结构弹性变形的影响。

对比图8与图10，可以发现刚柔混合模型臂架5质心振动幅度明显大于臂架1质心振动幅度。由此可知，考虑臂架系统柔性化的仿真结果，更加接近实际。

5 结束语

以某公司混凝土泵车臂架为例进行分析，确定其各节臂架固有频率和振型，建立臂架系统刚柔混合模型，对比刚柔混合模型与刚体模型的运动仿真结果，得出柔体仿真结果更加接近实际，为进一步动力学分析提供了理论依据。

[1]QC/T718-2004，混凝土泵车[S].

[2]田润利，吕彭民，贾剑峰.混凝土泵车臂架系统瞬态动力响应研究[J].建筑机械，2010，（3）：85-91.

[3]姜 涛，吕嘉宾，殷晨波.虚拟样机技术在混凝土泵车中的应用研究[J].工程机械，2006，37(6)：33-38.

[4]李增刚.ADAMS入门详解与实例[M].北京：国防工业出版社，2006.