混合制冷工质充注装置设计与分析计算

芮胜军 张 华 黄理浩

(上海理工大学制冷技术研究所 上海 200093)

1 引 言

制冷工质充注是制冷装置系统必不可少的环节，系统安装后，必须先进行检漏、抽真空和充注制冷工质，然后才能进行系统调试。本装置是在设计五级自动复叠制冷系统设计时提出的一种方案，自动复叠制冷循环的设计灵感源于经典复叠制冷循环，其原理为:单级压缩，多级分凝，自动复叠［1］。即混合工质经一次压缩后，按沸点高低顺序在多级分离器中逐级分离，使沸点最低的制冷工质进入蒸发器，制取预定的低温［2］。本实验需要充注的5种制冷工质分别为:R600a、R23、R14、R728 以及 R740，五级自动复叠制冷系统的工作原理如图1所示［3］。

2 充注装置具体实施方式

2.1 装置设计思路

制冷工质的充注方法常用的有电流法和称重法［4］，电流法是以压缩机的满载电流值为标准，充注过程中若充注的电流符合规定值，则表示制冷工质充注量合适。与电流法相比较，称重法直接将装有制冷工质的钢瓶置于台秤上，记下充注前后的质量，则可得到制冷工质的充注量，这种方法操作简单，测量准确，应用较广。但对于较高精度的台秤而言，其测量范围有限，只对其载重范围内的轻质钢瓶适用，对于大钢瓶则无法实现，例如本实验中涉及的R740、R728以及R14都是无法直接通过称重法进行充注的，为了解决这样的问题，一种方法就是将其导入小钢瓶。由于小钢瓶的耐压有限，这些低沸点气体常温下压力均较高，使每次充注量小，效率也降低了，而且容易造成泄漏和浪费，也有可能混杂进其它的气体成分，造成制冷工质纯度下降。

基于以上原因，利用工程热力学原理，设计出了一套制冷工质充注装置。所充制冷工质的基本热力性质如表1所示［5］，从该表中可以看出，R740、R728和R14的临界温度都较低，在环境温度下，且压力不太高时，气体的状态远离临界状态，可以近似的按照理想气体处理。

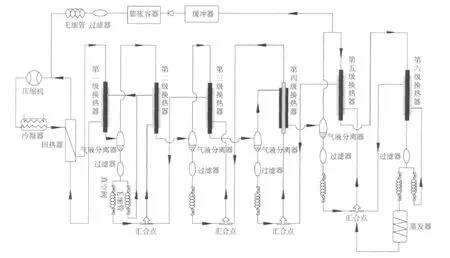
图1 五级自动复叠制冷系统图Fig.1 Five stage auto-cascade refrigeration system diagram

表1 所充制冷工质的基本热力性质Table 1 Basic thermodynamic properties of filling refrigerant

所设计的装置采用测温、测压的制冷工质充注方法，将制冷工质钢瓶与一中间储气罐相连接，然后再接到系统注入口。充注时记下环境温度和充注前后储气罐压力，根据温度、压力计算其密度。储气罐的容积已定，通过计算则可得到制冷工质的充注量。制冷工质充注方法又可分为低压充注法和高压充注法。低压充注法比较容易控制制冷工质的充注量，安全而且不易损坏部件，但充注时间较长，而且制冷工质呈气态，必须经过干燥器处理才能除去制冷工质中的微量水分;高压充注法充注时间短，但较难控制充注量，特别是小型设备，所以适用于制冷工质充注量较大的制冷系统。由于本装置是在五级自动复叠制冷系统设计时提出的一种方案，所充制冷工质较少，通常为几十克，所以适宜采用低压充注法。

所设计的充注装置结构如图2所示［4，6］。充注系统是由虚线内的部分构成，包括箱体、储气罐、干燥过滤器、压力表、毛细管以及两个手动调节阀。充注箱体左侧通过一段毛细管连接制冷工质钢瓶，使用毛细管主要有两个方面的原因:首先，如果钢瓶内的气体压力过高，阀门打开瞬间极易损坏压力表;其次，制冷工质气体压力过大，充注速度过快，不易控制充注量。充注箱体右侧与压缩机的低压端相连。干燥过滤器内装有活性碳和变色硅胶，中间储气罐通过毛细管接有精密压力表。两个手动调节阀分别位于箱体的入口端和出口端。

图2 充注装置系统图Fig.2 Schematic diagram of filling device system

2.2 制冷工质充注过程

所设计的充注装置分两个充注线路，A线路为R740、R728以及R14的充注流程，B线路为其余轻质钢瓶直接用高精度电子台秤采用称重法进行充注。多流程混合制冷工质的充注方法如图3所示。

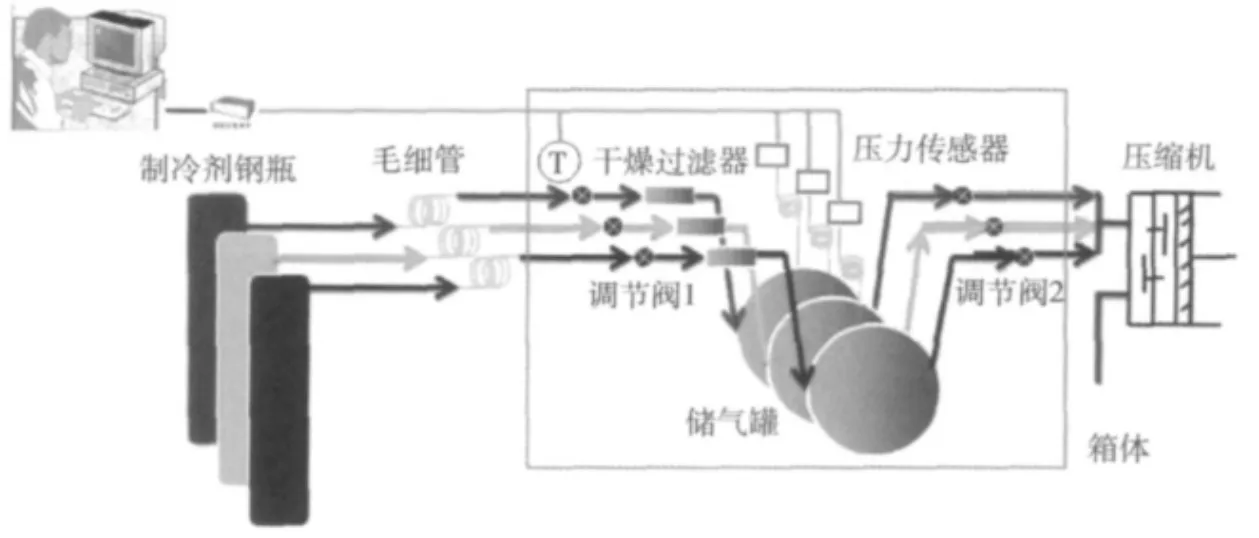
图3 多流程混合制冷工质的充注方法Fig.3 Filling method of multi-process mixed refrigerant

A流程的原理为:将制冷工质钢瓶与一中间储气罐相连接再接到系统注入口。充注时记下环境温度和充注前后储气罐压力，根据温度、压力分别算出其对应的比体积，而储气罐的容积已定，计算即得制冷工质的充注量。手动调节阀1打开，手动调节阀2关闭，打开制冷工质钢瓶，制冷工质由左侧入口通过毛细管缓慢进入充注箱，经过干燥过滤器干燥后，进入储气罐，记录环境温度T0。当储气罐压力到达一定数值的时候，关闭手动调节阀1。记录此时压力表数值P1。打开手动调节阀2，向右侧的制冷系统充注制冷工质，当压力表读数降到一定数值的时候，关闭手动调节阀2，再记下此时压力表的数值P2，完成一次充注。

B流程的原理为:将钢瓶与压缩机低温端进行连接，电子称打开，记录此时电子称稳定读数m1;缓缓旋开钢瓶阀门，观察电子称读数至适当数值关闭阀门，记录电子称稳定读数m2;则充注制冷工质质量为:Δm=m1－m2。

3 制冷工质充注量的计算

3.1 用理想气体计算

根据前文的介绍，所充制冷工质气体R740、R728和R14的状态远离临界状态，可以近似的按照理想气体处理。应用理想气体状态方程［7］:

对质量为m(千克)的气体:

则:

上式中:p为制冷工质的绝对压力，MPa;V为储气罐的容积，m3;m为工质的质量，kg;R为每种气体的气体常数，J/(kg·K)，T0为环境温度，K;Δp为充注前后的压力差，MPa;Δm为充注制冷工质的质量，kg。

在本实验中储气罐的容积为0.001 m3，环境温度T0为291.15 K，所以充注的制冷工质质量与充注前后制冷工质的压力差成正比。本实验中的计算结果如表2所示，根据所充制冷工质的压差就可以得到其质量。

表2 所充制冷工质的质量基数(1)Table 2 Basic quality of filling refrigerant(1)

3.2 用REFPROP软件按照实际气体方程计算

应用美国国家标准与技术研究院的制冷工质物性计算软件 REFPROP8.0［8-9］，按照实际气体方程，计算出环境温度为T0、压力为p1时制冷工质的密度ρ1。同样计算出T0环境温度下，压力为p2时，制冷工质的密度 ρ2。

又因为储气罐的容积V一定，可以分别求出压力为p1和p2时储气罐中制冷工质的质量m1、m2:

则制冷工质充注量为:

m1、m2为充注前后储气罐中制冷工质的质量，kg;ρ2、ρ1为充注前后储气罐中制冷工质的密度;V为储气罐的容积，m3，Δm为充注制冷工质质量，kg。

表3为按照实际气体方程CSD方程、MBWR方程、Helmhltz自由能状态方程、P-T方程、M-H方程等计算出的结果。

表3 所充制冷工质的质量基数(2)Table 3 Basic quality of filling refrigerant(2)

由表2和表3可以看出，两种方法对于R740和R728计算出的充注量几乎没有差别。而对于R14，两种方法计算出的误差为1.24%，这主要是因为表2按照理想气体状态方程计算，而表3按照实际气体方程CSD方程、MBWR方程、Helmhltz自由能状态方程、P-T方程、M-H方程等计算，相对准确一些。可以预测，对于R600a和R23，通过这两种方法计算出的结果差别更大，因为其临界状态温度与环境温度差别较小，不能作为理想气体，必须按照实际气体进行计算。

4 结 论

混合制冷工质充注装置是多组分制冷工质系统的必要设备，测量原理是通过计量定容器内气体在充注前后的压差根据工质物性计算出充注质量。特点是容积固定，温度影响小(1/300)且可补偿，压力测量精度高，计量精度高。装置简单，解决多元混合制冷工质充注难题;制冷工质充注精度高，精度到0.01 g;加工、使用和控制简便;对充注的制冷工质有过滤和干燥功能。

同现有技术相比，此制冷工质充注系统的显著优点是:解决了一些制冷系统因制冷工质钢瓶过重，而难以准确计算制冷工质充注量的问题。具有制冷工质充注精度高，加工、使用和控制简便以及维修方便等优点。

1 杜 凯，廖开蒙.自然复叠制冷系统初探［J］.低温工程，2002，127(3):29-33.

2 曹 丹，王 勤，陈光明.一种新型的自动复跌制冷循环［J］.低温工程，2003，135(5):49-54.

3 芮胜军，张 华，张海东，等.自动复叠制冷系统混合工质运行成分分析［C］.2011年中国制冷学会学术年会论文集，南京:2011.

4 刘红绍.单级与自动复叠耦合制冷系统的试验研究［D］.上海:上海理工大学，2008.

5 陈光明，陈国邦.制冷与低温原理(第2版)［M］.北京:机械工业出版社，2010.

6 张 华，刘训海，刘红绍，等.一种高精度制冷工质充灌装置:中国，200710047016.8［P］.2008-03-05.

7 沈维道，童钧耕.工程热力学(第4版)［M］.北京:高等教育出版社，2007.

8 Alexandrow A A，Crigoriev B A，Ustjuzhanin E E，et al.Some modelling of cooling cycles used in individual and mixed refrigerants［J］.Fluid Phase Equilibria，2000，174:178-189.

9 Eric W Lemmon，Reiner Tillner-Roth.A Helmholtz energy equation of state for calculating the thermodynamic properties of fluid mixtures［J］.Fluid Phase Equilibria，1999，165:1-21.