一种新的具有光滑二次函数多涡卷混沌系统及其FPGA实现

黄 沄，罗小华，张 鹏

(1.重庆邮电大学资产管理处，重庆 400065;2.重庆邮电大学光电学院，重庆 400065;3.重庆邮电大学教务处，重庆 400065)

0 引言

由于多涡卷混沌系统比传统的单涡卷和双涡卷混沌系统具有更为复杂的动力学行为，在保密通信和信息隐藏等领域具有更好的应用前景，因此，构造新的多涡卷混沌系统及其电路实现已成为目前混沌研究领域的一个热点。

1993年，Sukens等［1］通过增加非线性函数曲线的转折点发现了多涡卷混沌吸引子，从此人们展开了对多涡卷混沌系统的研究。起初，都集中在研究只有一个非线性函数的多涡卷混沌系统，得到单方向多涡卷混沌吸引子［1－5］;2002年，文献［6］提出了在多涡卷混沌系统中引入两个或多个的相同类型非线性函数，获得了网格多涡卷混沌吸引子。之后又相继提出大量的网格多涡卷混沌系统［7－11］，扩展和补充了多涡卷混沌系统;2009年，一种含有不同类型的非线性函数的网格多涡卷混沌系统被提出并研究［12］，进一步补充和完善了多涡卷混沌系统。然而，对于含有光滑二次函数的多涡卷混沌系统还未见报道，显然有必要对这类多涡卷混沌系统进行研究。

在文献［9］的多涡卷混沌系统上添加了一个光滑二次函数，并进行了适当的修改，得到了一个新的具有光滑二次函数的多涡卷混沌系统，系统中同时含有光滑二次函数和三角波函数。分析了系统的基本动力学行为，包括平衡点、Lyapunov指数谱、分岔图、相图和Poincaré截面。最后，利用FPGA进行了硬件实验，硬件实验结果与数值仿真结果相一致。

1 光滑二次函数的多涡卷混沌系统

文献［9］的产生单方向多涡卷混沌吸引子的系统的状态方程为

在(3)式和(4)式中，取a=0.2，b=0.8，c=2，d=0.25，β=0.02，m=1，2，…，M。系统(3)能产生 M+1个涡卷。当 M=1，2，3，4 时，系统(2)产生的2，3，4和5涡卷混沌吸引子如图1所示。

图1 系统(3)在y－z平面上的多涡卷吸引子Fig.1 Multi－scroll chaotic attractors of system(3)in y － z plane

2 系统的基本动力学行为

2.1 平衡点及其稳定性分析

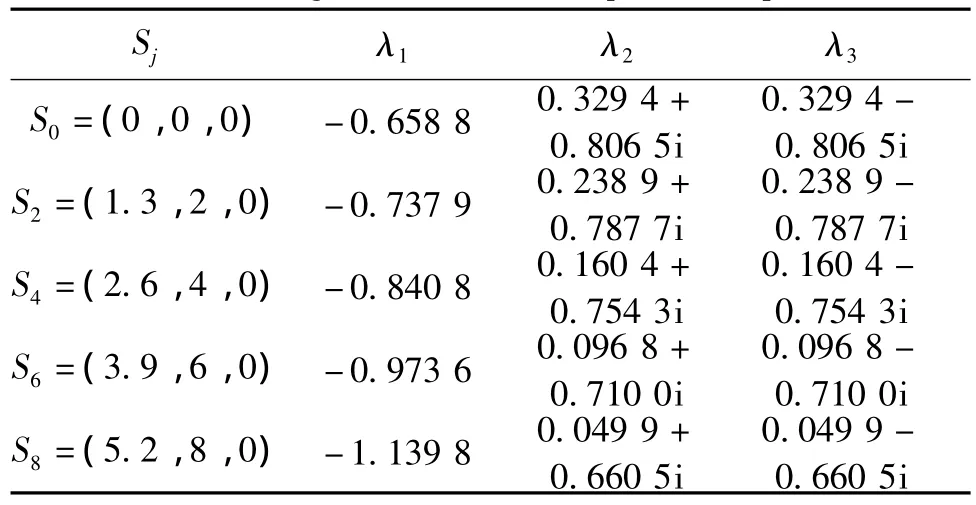
表1 涡卷平衡点的特征值Tab.1 Eigenvalue of scroll equilibrium point

从表1可知，λ1为负实根，λ2和λ3是一对具有正实部的共轭复根，因此，系统(3)的所有涡卷平衡点都是不稳的鞍焦点。

2.2 Lyapunov指数谱和分岔图

取M=4，系统(3)随二次函数项的系数a变化的Lyapunov指数谱和分岔图如图2所示。

图2 系统(3)的lyapunov指数谱和分岔图Fig.2 Lyapunov exponent spectrum of system(3)and its bifurcation diagram

2.3 Poincaré截面

以五涡卷为例，对系统(3)的Poincaré截面进行数值模拟。取通过所有平衡点的面x－0.65y=0作为Poincaré截面，其在y－z平面上的Poincaré映射如图3所示。从图3可以看出，截面上的Poincaré映射是成片的密集点且分成5个部分，而每个部分的点向多个方向散开，表明系统具有复杂的动力学特性。

图3 系统(3)的Poincaré截面Fig.3 Poincarémaps of system(3)

3 系统的FPGA实现

基于 IEEE－754 标准和 FPGA 技术［13］，对系统(3)进行了硬件实验。

在用FPGA对系统的电路设计之前，必须对系统进行离散处理，采用Euler算法对系统(3)作离散化处理，系统(3)离散化后的方程为

图4 利用FPGA对系统(6)进行硬件设计的模块简图Fig.4 Module diagram of hardware designed for system(6)based on FPGA

图4中，开关K置于位置1时，选择系统初始值;置于位置2时，选择系统迭代值。开关K1，K2，K3，K4控制系统产生涡卷的个数，当开关K1置于位置1，K2置于位置2，K3置于位置2，K4断开时，FPGA能产生二涡卷，如图5a所示;当开关K1和K2置于位置1，K3置于位置2，K4断开时，FPGA能产生三涡卷，如图5b所示;当开关K1，K2和K3置于位置1，K4断开时，FPGA能产生四涡卷，如图5c所示;当开关 K1，K2和 K3置于位置1，K4闭合时，FPGA能产生五涡卷，如图5d所示。

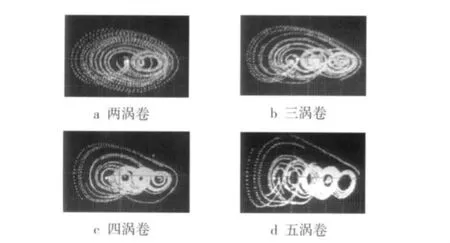
图5 FPGA产生的多涡卷混沌吸引子Fig.5 Multi－scroll chaotic attractor generated by FPGA

从图1和图5可以看出，利用FPGA产生的多涡卷吸引子与数值仿真结果相一致。

4 结论

构造了一个含光滑二次函数和分段函数的多涡卷混沌系统。分析了系统的平衡点、Lyapunov指数谱和分岔图，对系统的多涡卷混沌吸引子和Poincaré截面的数值仿真，呈现出了其复杂的动力学特性。最后，利用FPGA对系统进行了硬件实验，其结果与数值仿真结果相一致。另外，值得注意的是对该系统的构造方法还可用于其他多涡卷混沌系统的设计而不失一般性。

［1］SUYKENS JA K，VANDEWALLE J.Generation of ndouble scrolls(n=1，2，3，4，…)［J］.IEEE Trans Circuits Syst I，1993，40(11):861－867.

［2］SUYKENS JA K，HUANG A，CHUA L O.A family of n－scroll attractors from a generalized Chua's circuit［J］.Int JElectron Commun，1997，51(8):131－138.

［3］王发强，刘崇新.一类多折叠环面多涡卷混沌吸引子的仿真研究［J］.物理学报，2007，56(4):1983－1987.

WANG Fa－qiang，LIU Chong－xin.Simulation of a family of multi－folded torus and multi－scroll chaotic attractors［J］.Acta Phys Sin，2007，56(4):1983－1987.

［4］罗小华，李华青，代祥光.一类多涡卷混沌吸引子及电路设计［J］.物理学报，2008，57(12):7511－7516.

LUO Xiao－hua，LIHua－qing，DAIXiang－guang.A family ofmulti－scroll chaotic attractors and its circuit design［J］.Acta Phys Sin，2008，57(12):7511－7516.

［5］ZHANG Chao－xia，YU Si－min.Design and implementation of a novelmulti－scroll chaotic system［J］.Chin Phys B，2009，18(1):119－129.

［6］YALCIN M E，SUYKENS J A K，VANDEWALLE J.Families of scroll grid attractors［J］.Int JBifurc Chaos，2002，12(1):23－41.

［7］CAFAGNA D，GRASSI G.Hyperchaotic coupled Chua circuits:An approach for generating new n × m－scroll attractors［J］.Int J Bifurc Chaos，2003，13(9):2537－3550.

［8］LÜ J，HAN F，YU X，et al.Generating 3－Dmulti－scroll chaotic attractors:A hysteresis series switching method［J］.Automatica，2004，40(10):1677－1687.

［9］禹思敏.用三角波序列产生三维多涡卷混沌吸引子的电路实验［J］. 物理学报，2005，54(4):1500－1509.

YU SM.Circuit implementation for generating three－dimensionalmulti－scroll chaotic attractors via triangular wave series［J］.Acta Phys Sin，2005，54(4):1500－1509.

［10］包伯成，刘中，许建平，等.基于Colpitts振荡器模型生成的多涡卷超混沌吸引子［J］.物理学报，2010，59(3):1540－1548.

BAO Bo－cheng，LIU Zhong，XU Jian－ping，etal.Generation ofmulti－scroll hyperchaotic attractor based on Colpitts oscillatormodel［J］.Acta Phys Sin，2010，59(3):1540－1548.

［11］LUO Xiao－hua，TU Zheng－wei，LIU Xi－rui，et al.Im lementation of a novel two－attractor gridmulti－scroll chaotic system［J］.Chin Phys B，2010，19(7):070510.

［12］张朝霞，禹思敏.用时滞和阶跃序列组合生成网格多涡卷蔡氏混沌吸引子［J］.物理学报，2009，58(1):120－130.

ZHANG Chao－xia，YU Si－min.Generation of grid multiscroll Chua's chaotic attractors with combination of hysteresis and step series［J］.Acta Phys Sin，2009，58(1):120－130.

［13］周武杰，禹思敏.基于IEEE－754标准和现场可编程门阵列技术的混沌产生器设计与实现［J］.物理学报，2008，57(8):4738－4747.

ZHOU Wu－jie，YU Si－min.Design and implementation of chaotic generators based on IEEE－754 standard and field programmable gate array technology［J］.Acta Phys Sin，2008，57(8):4738－4747.

(编辑:田海江)