噪声连续波雷达脉压输出主旁瓣比推导与分析

程院兵，张卫，顾红，苏卫民

(南京理工大学 电子工程与光电技术学院，江苏 南京210094)

0 引言

近年来，噪声连续波雷达(Noise Continuous Wave Radar，NCWR)被广泛研究应用于搜索雷达、合成孔径雷达(SAR)、逆合成孔径雷达(ISAR)、防撞雷达、穿地探测雷达和穿墙成像雷达等诸多领域［1－5］。NCWR 具有图钉形模糊函数，使其具有无测距测速模糊、良好的距离速度分辨率和精度等优点［6］。另外，NCWR 的低截获概率(LPI)、低截获识别概率(LPID)和良好的电子反对抗能力(ECCM)使其在复杂的电子战环境中更具优势［7］。

然而，噪声连续波雷达信号属于多普勒敏感信号，使其应用受到限制，因此定量描述NCWR 脉压输出主旁瓣比与脉压长度、多普勒频率和回波信噪比等参数的关系，对NCWR 参数选取、旁瓣抑制及多普勒容限扩展等均具有重要指导意义。一些学者对NCWR 脉压输出旁瓣特性进行了研究［8－9］。文献［8］指出对于静止目标，脉压输出主瓣均方旁瓣比等于脉压长度，但没有给出其与多普勒频率的关系;文献［9］通过统计方法指出对于静止目标，脉压输出主瓣峰值旁瓣比随脉压长度的增加而增加，但没有给出定量关系。本文在考虑多普勒频率和回波信噪比情况下，通过对脉压输出旁瓣的概率分布和二阶统计量分析，推导了NCWR 脉压输出主瓣均方旁瓣比和主瓣峰值旁瓣比的数学表达式。对影响主瓣均方旁瓣比和主瓣峰值旁瓣比的参数进行了分析和讨论。由于发射信号本身为随机信号，所以脉压输出主瓣均方旁瓣比和主瓣峰值旁瓣比实际上是统计值，分别称之为统计主瓣均方旁瓣比(Statistical Mainlobe to Mean Square Sidelobe Ratio，SMMSSR)和统计主瓣峰值旁瓣比(Statistical Mainlobe to Peak Sidelobe Ratio，SMPSR)。计算机蒙特卡罗实验结果与理论推导结果能够很好的吻合，验证了本文结论的正确性。

1 信号模型及脉压处理

噪声连续波雷达发射信号s(t)表示为

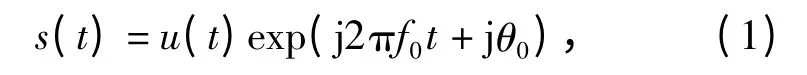
式中:u(t)=x(t)+jy(t)为信号复包络，x(t)和y(t)是服从均值为0，方差为σ2的窄带高斯白噪声，且x(t)与y(t)不相关;f0为发射信号载频;θ0为固定初始相位。

假设存在延时为T，多普勒频率为fd的单个点目标，其回波表达式为

将发射信号s(t)延时Tref作为参考信号，表示为

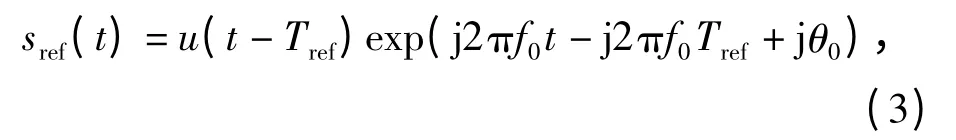
回波信号与参考信号相关输出表示为

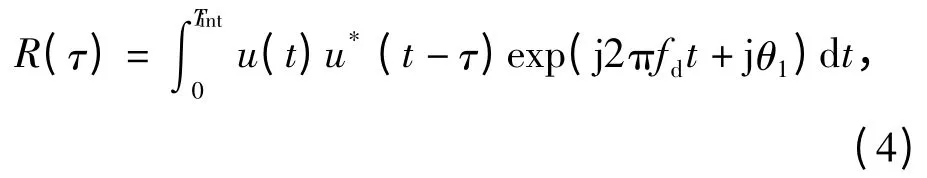
式中:τ =Tref－T;θ1=2πf0τ 为固定相位;* 表示共轭运算;Tint为相关处理时间，须满足vTint≤c/(2B)，其中v 为目标径向速度;B 为发射信号带宽;c 为光速。假设式(4)中相位项exp(j2πfdt +jθ1)在某一较小时间间隔ΔTint内变化较小，将相关处理时间Tint划分为M 个连续的时长为ΔTint的片段，分别对每个片段进行脉压，然后再对M 次脉压结果沿同一距离单元做离散傅里叶变换(DFT)可得到距离－多普勒二维处理结果。这儿我们只研究其中一个片段脉压输出的统计特性，其脉压处理框图如图1所示。将采样得到的时长为Tint的基带回波序列作为一帧数据，考虑对第l 帧回波中第m 个片段进行脉压，写成离散形式

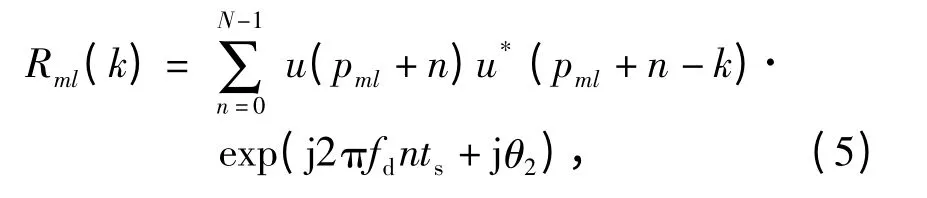
式中:pml=(l－1)NM +(m－1)N 为第l 帧回波中第m 个数据片段的起始位置;l=1，2，…为帧数据的索引;m =1，2，…M 为一帧回波中进行脉压处理的数据片段的索引;ts=1/B 为采样间隔;N =BΔTint为脉压长度;k=0，1，…K－1 为相对延时τ 关于采样间隔为单位划分的距离单元数，K 为需要观测的距离单元数;θ2=2πfdpmlts+θ1为第l 帧回波数据中第m 个片段的初始相位。

图1 噪声连续波雷达脉压处理框图Fig.1 Block diagram of pulse compression for NCWR

2 脉压输出统计主瓣均方旁瓣比推导

下面在式(5)的基础上推导脉压输出统计主瓣均方旁瓣比的数学表达式。当k=0 时，Rml(k)为脉压输出峰值，用Vp表示。由于u(n)是一复随机序列，所以Vp是一统计值。当N≫1 时，Vp等于其均值，表示为

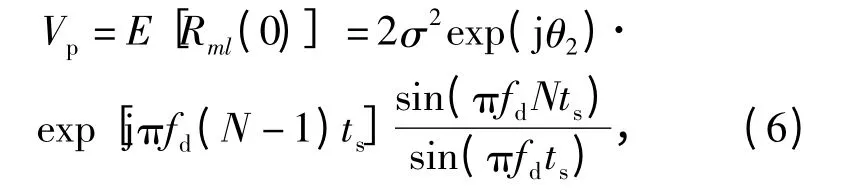
式中:E(·)表示取均值。当k≠0 时，Rml(k)为脉压输出旁瓣，其均值为0，方差为

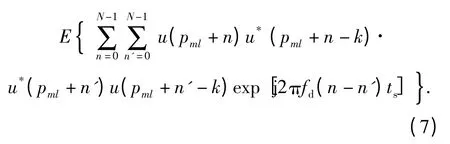
上式仅当n=n'时不为0，此时式(7)可改写为

则脉压输出统计主瓣均方旁瓣比(SMMSSR)可表示为

下面对考虑回波噪声情况下的SMMSSR 进行分析，此时式(5)可写为

式中:ε(n)=ε1(n)+jε2(n)为复加性噪声，ε1(n)和ε2(n)为服从均值0，方差为σ2n的高斯白噪声，且x(n)、y(n)、ε1(n)和ε2(n)之间均互不相关。此时脉压输出峰值为

脉压输出旁瓣均值为0，类似式(7)到式(8)推导可得其方差为

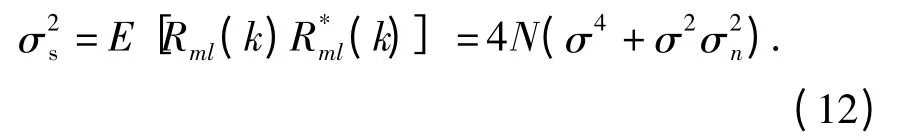
由式(11)和式(12)可以看出多普勒频率仅影响脉压输出峰值，回波噪声仅影响旁瓣功率，使旁瓣基底抬高。最后，得到噪声连续波雷达脉压输出统计主瓣均方旁瓣比可表示为

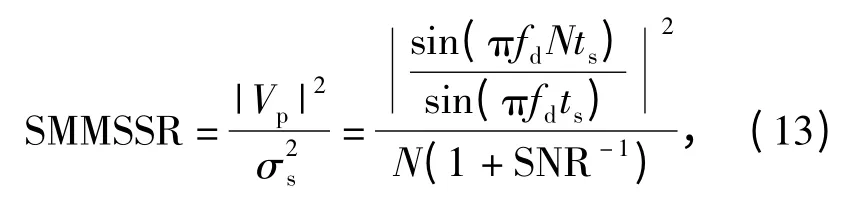
式中:SNR=σ2/σ2n为回波信噪比。由上式可以看出统计主瓣均方旁瓣比与脉压长度、回波信噪比和多普勒频率与采样间隔的乘积有关，与回波固定相位和目标延时无关(即，与m，l 和τ 无关)。特别的，对于静止目标，在不考虑回波加性噪声情况下，统计主瓣均方旁瓣比等于脉压长度，与文献［8］结论一致。

3 脉压输出统计主瓣峰值旁瓣比推导

根据式(10)，脉压输出旁瓣可表示为

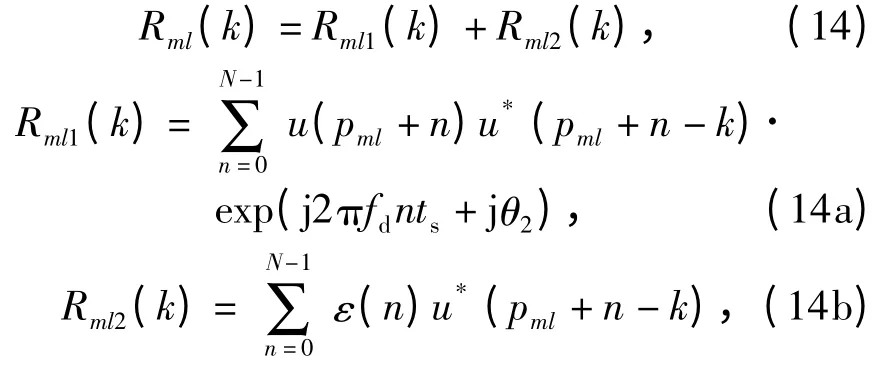
式中:k≠0.可将Rml1(k)看作是一个噪声序列通过一个窄带FIR 滤波器的输出，满足“宽带输入窄带输出”过程，则Rml1(k)的实部和虚部均服从正态分布［10］。可将Rml2(k)看作高斯信号序列ε(n)通过系数为序列u(pml+n)的共轭倒置的线性滤波器的输出，则Rml2(k)的实部和虚部均服从正态分布［11］。因此，脉压输出旁瓣的实部和虚部均服从正态分布。用序列S 表示式(14)，写成S =Sr+j Si，其中Sr和Si分别为S 的实部和虚部，均服从正态分布，其表达式为Sr=Re［Rml(k)］和Si=Im［Rml(k)］.由式(5)可得Sr和Si的均值均为0，方差均等于=2N(σ4+σ2σ2n)，则均服从标准正态分布，其中Sr和Si分别为Sr和Si的元素。令z =|S|2/σ2hs，S 为序列S 的任一元素，则可知z 服从自由度为2 的χ2分布，其概率密度为

图2给出了在脉压长度N =1 000，观测距离单元数K=5 000，目标延迟距离单元数r=160，回波信噪比SNR=0 dB，多普勒频率fd=1/(10Nts)，仿真信号是均值为0，方差σ2=10，带宽B =50 MHz 的平稳高斯白噪声条件下，脉压输出旁瓣的概率密度直方图。图中直方图进行了归一化处理，使其具有单位面积。假设z 的峰值zp仅出现在K－1 个距离旁瓣单元中的一个，其概率密度为1/(K－1)，则有

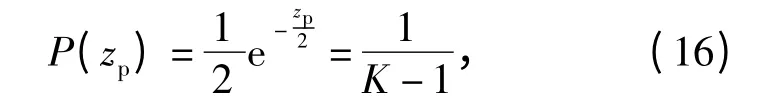
由上式可得zp=2ln［(K－1)/2］，则脉压输出峰值旁瓣电平|Sp|为

结合式(11)和式(17)得到统计主瓣峰值旁瓣比(SMPSR)表达式为

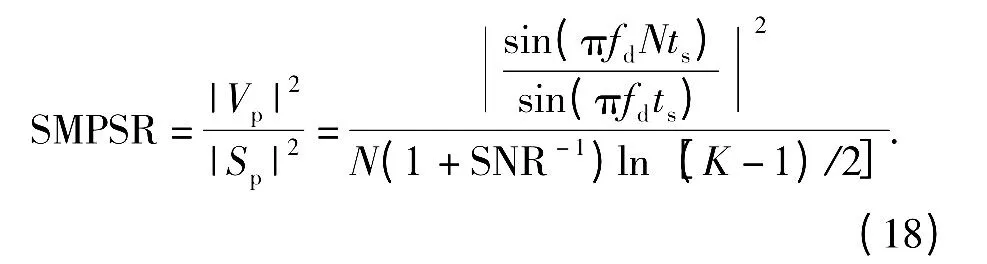
从上式可以看出统计主瓣峰值旁瓣比与脉压长度、回波信噪比、多普勒频率与采样间隔的乘积和观测距离单元数有关，与回波固定相位和目标延时无关(即，与m，l 和τ 无关)。特别的，对于静止目标，在不考虑回波加性噪声情况下，统计主瓣峰值旁瓣比等于N/ln［(K－1)/2］，当观测距离单元K 固定时，SMPSR 随脉压长度N 的增加而增加，与文献［9］结论一致。下面讨论观测距离单元数K 的取值范围，一般我们认为统计主瓣峰值旁瓣比小于统计主瓣均方旁瓣比，根据式(13)和式(18)可得

式中:「·⏋表示向上取整。上式为观测距离单元数K 的下界，但为了保证足够的观测距离单元样本数，一般要求K ≫1.假设要求SMPSR 的门限值为α(dB)，令须有SMPSR ＞β，可得

4 仿真结果与分析

本节通过计算机仿真验证式(13)和式(18)的正确性，脉压处理采用延时相关处理方法［5，8－10］，其流程框图如图1所示，将参考信号按距离单元逐个延时后分别与回波信号做相乘累加处理，即可得到每个距离单元的脉压结果。通过4 个仿真实验分别验证SMMSSR 和SMPSR 与脉压长度、多普勒频率、回波信噪比和观测距离单元数的关系。仿真信号是均值为0，方差σ2=10 的平稳复高斯白噪声，带宽B=50 MHz，采样间隔ts=1/B，单个点目标延迟距离单元数r=160，对第一帧回波数据的第一个片段进行脉压，即l=m=1.

实验1:图3给出了在不考虑回波加性噪声，多普勒频率fd=0，观测距离单元数K =1 000 情况下，SMMSSR 和SMPSR 与脉压长度的曲线关系。脉压长度N 的取值为N =10，20，40，80，…，20 480，进行了1 000 次蒙特卡罗实验。从图3可以看出，仿真结果与理论结果能很好的吻合。SMMSSR 误差小于0.3 dB，SMPSR 误差小于1 dB;SMMSSR 和SMPSR均随着脉压长度的增加线性增加，SMMSSR 近似等于N，SMPSR 近似等于N/ln［(K－1)/2］.因此，可通过增加脉压长度提高脉压输出主旁瓣比，且对相同的脉压长度，SMMSSR 比SMPSR 高8 dB，近似等于ln［(K－1)/2］.

实验2:图4给出了在不考虑回波加性噪声，脉压长度N =1 000，观测距离单元数K =1 000 情况下，SMMSSR 和SMPSR 与归一化多普勒频率的曲线关系。最大多普勒频率fdmax为1/(2Nts)的1.9 倍，多普勒频率从0 到fdmax之间以0.05fdmax的步长增加，进行了1 000 次蒙特卡罗实验。从图4可以看出，仿真结果与理论结果能很好的吻合。SMMSSR误差小于0.3 dB，SMPSR 误差小于1 dB;随着多普勒频率的增大，主峰减小，从而使SMMSSR 与SMPSR 均减小。当归一化多普勒频率为0.47 时，SMMSSR 与SMPSR 均比多普勒为0 时降低了3 dB;当归一化多普勒频率增大到0.97 时，脉压输出主峰被峰值旁瓣淹没，不能检测到目标。另外，相比伪码调相连续波雷达［10］，NCWR 的多普勒敏感性有所改善。

图3 统计主瓣均方旁瓣比和统计主瓣峰值旁瓣比与脉压长度的关系Fig.3 The SMMSSR and SMPSR vs.N

实验3:图5给出了在多普勒频率fd=0，脉压长度N =1 000，观测距离单元数K =1 000 情况下，SMMSSR 和SMPSR 与回波信噪比的曲线关系。回波信噪比从－30 dB 到30 dB 之间以2 dB 的步长增加，进行了1 000 次蒙特卡罗实验。从图5可以看出，当信噪比低于－22 dB 时，SMMSSR 的仿真结果与理论出现较大偏差，脉压输出主峰被峰值旁瓣淹没，不能检测到目标;当信噪比大于－22 dB 时，仿真结果与理论结果能很好的吻合，SMMSSR 误差小于0.3 dB，SMPSR 误差小于1 dB.随着信噪比的增加，SMMSSR 和SMPSR 均增加。当信噪比大于－20 dB小于0 dB 时，SMMSSR 和SMPSR 与信噪比为线性增加关系;当信噪比大于10 dB 时，SMMSSR和SMPSR 分别达到各自的稳定值，近似等于无加性噪声时的值，此时可认为回波噪声对SMMSSR 和SMPSR 几乎没有影响，旁瓣主要取决于发射信号脉压后的自身杂波。

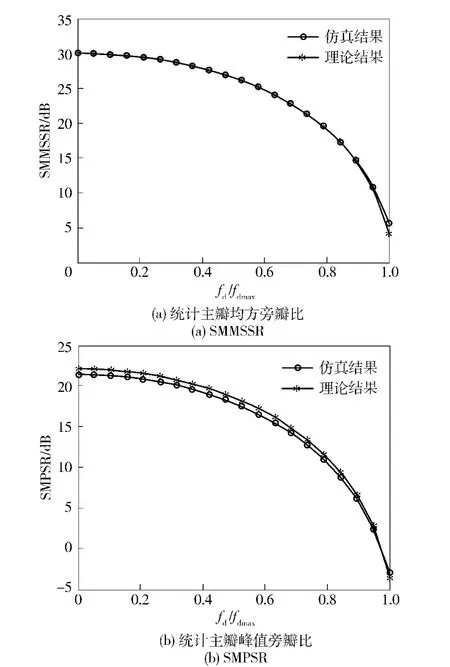
图4 统计主瓣均方旁瓣比和统计主瓣峰值旁瓣比与归一化多普勒频率的关系Fig.4 The SMMSSR and SMPSR vs.fd/fdmax

实验4:表1给出了在多普勒频率fd= 1/(10Nts)，SNR=0 dB，脉压长度N=1 000，观测距离单元数K =300，3 000，30 000 情况下，SMMSSR 和SMPSR 的值。进行了1 000 次蒙特卡罗实验。从表1可以看出，仿真结果与理论结果能很好的吻合，SMMSSR 误差小于0.3 dB，SMPSR 误差小于1 dB，观测距离单元数对SMMSSR 几乎没有影响。K =30 000时的SMPSR 比K =300 时小了约2.7 dB，与式(18)中SMPSR 随着K 的增加以对数形式缓慢减小相一致。同时需要指出NCWR 的观测距离单元数只受式(20)的限制，脉压输出不存在距离模糊，较大的观测距离单元数会增加峰值旁瓣电平，从而增加虚警概率。

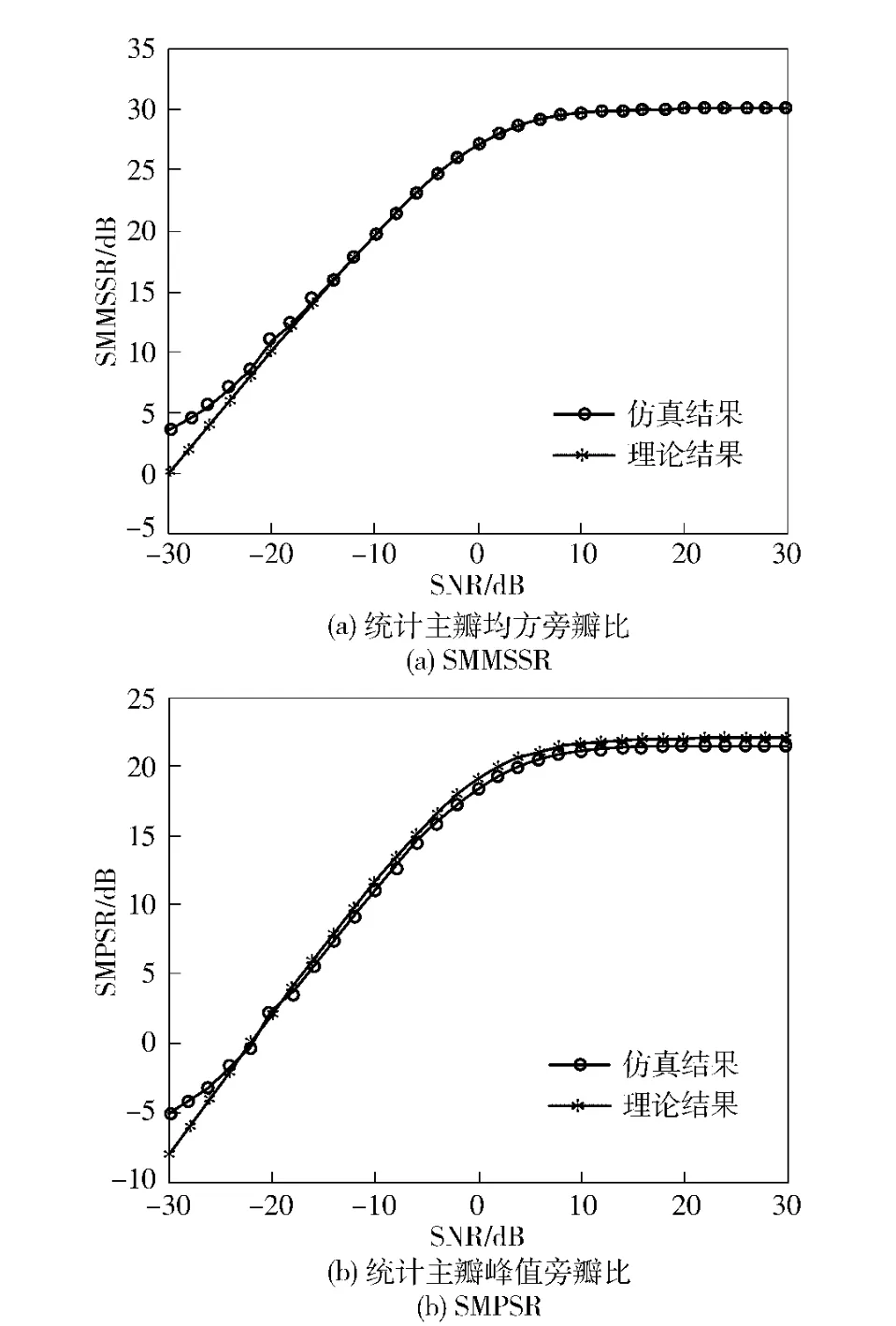
图5 统计主瓣均方旁瓣比和统计主瓣峰值旁瓣比与回波信噪比的关系Fig.5 The SMMSSR and SMPSR vs.SNR

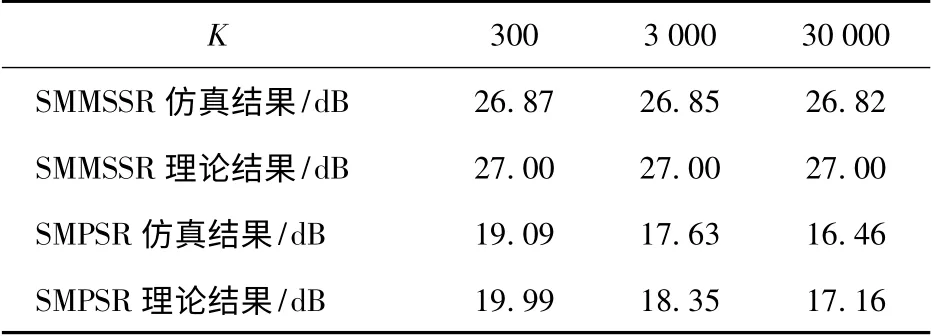
表1 统计主瓣均方旁瓣比和统计主瓣峰值旁瓣比与观测距离单元数的关系Tab.1 The SMMSSR and SMPSR vs.K

5 结论

本文在考虑多普勒频率和回波噪声情况下，通过对噪声连续波雷达脉压输出旁瓣的概率分布和二阶统计量分析，推导了噪声连续波雷达脉压输出统计主瓣均方旁瓣比和统计主瓣峰值旁瓣比的数学表达式，为定量分析噪声连续波雷达脉压输出主旁瓣比与脉压长度、多普勒频率和回波信噪比等参数的关系提供了理论依据，这对噪声连续波雷达参数选取、旁瓣抑制及多普勒容限扩展等问题的研究具有重要的指导意义和参考价值。计算机蒙特卡罗实验结果与理论推导结果式(13)和式(18)能很好的吻合，验证了本文结论的正确性。

References)

［1］ Liu Guo－sui，Gu Hong，Su Wei－min，et al.Random signal radar－A winner in both the military and civilian operating environments［J］.IEEE Transactions on Aerospace and Electronic Systems，2003，39(2):489－498.

［2］ Lukin K A，Narayanan R M.Fifty years of noise radar［C］∥11th International Radar Symposium(IRS).Vilnius，Lithuania，2010:1－2.

［3］ Tarchi D，Lukin K，Fortuny－Guasch J，et al.SAR Imaging with noise radar［J］.IEEE Transactions on Aerospace and Electronic Systems，2010，46(3):1214－1225.

［4］ Xu Yi，Narayanan R M，Xu Xiaojian，et al.Polarimetric processing of coherent random noise radar data for buried object detection［J］.IEEE Transactions on Geoscience and Remote Sensing，2001，39(3):467－478.

［5］ Hong Wang，Narayanan R M，Zheng Ou Zhou.Through－wall imaging of moving target using UWB random noise radar［J］.IEEE Antennas and Wireless Propagation Letters，2009，8:802－805.

［6］ 刘国岁，顾红，苏卫民.随机信号雷达［M］.北京:国防工业出版社，2005:26－43.LIU Guo－sui，GU Hong，SU Wei－min.Random signal radar［M］.Beijing:National Defence Industry Press，2005:26－ 43.(in Chinese)

［7］ Pace P E.Detecting and classifying low probability of intercept radar［M］.London:Artech House Press，2009:34－35.

［8］ Axelsson S R J.On the theory of noise Doppler radar［C］∥Proceedings of International Geoscience and Remote Sensing Symposium，Honolulu，2000:856－860.

［9］ 张先义，苏卫民，顾红.随机噪声超宽带雷达信号性能分析［J］.兵工学报，2007，28(5):557－560.ZHANG Xian－yi，SU Wei－min，GU Hong.Performance analysis for random noise ultra－wideband radar signal［J］.Acta Armamentarii，2007，28(5):557－560.(in Chinese)

［10］ 陈金立，顾红，苏卫民.伪码调相连续波雷达的脉压主旁瓣比数学分析［J］.兵工学报，2008，29(10):1203－1209.CHENG Jin－li，GU Hong，SU Wei－min.Mathematical analysis of main－to－sidelobe ratio after the pulse compression in pseudorandom code phase modulation continuous wave radar［J］.Acta Armamentarii，2008，29(10):1203－1209.(in Chinese)

［11］ Robert M G，Lee D D.An introduction to statistical signal processing［M］.Cambridge:Cambridge University Press，2004:381－382.