给定辐射时间限制下的雷达辐射时机最优规划研究

吴巍，王国宏，李世忠

(海军航空工程学院 信息融合研究所，山东 烟台264001)

0 引言

现代战场环境中总存在着各种敌方的侦察和干扰，为了有效的保护自身安全，需要限制雷达电磁辐射时间以减少雷达被侦察的概率，而雷达探测目标时又必须向外辐射电磁波，这就存在着不可抗拒的矛盾。为了减少雷达辐射，在限定雷达辐射时间的情况下，如何对雷达辐射时机进行规划，使得目标跟踪的状态估计精度最高，是一个有待研究的问题。

对于雷达的辐射规划问题，国内外学者做了一些相关的研究。文献［1］利用优化目标函数—雷达/ESM 联合估计的可拉美－罗(Cramer－Rao)下限来研究雷达规划问题，利用数值计算方法得到雷达辐射规划原则。文献［2～4］分别研究了几种自适应的雷达数据更新算法。文献［5］提出了等间隔辐射控制和实时辐射控制两种机载雷达辐射控制方法。文献［6－9］利用雷达、红外同时开机时的量测信息，构造出一组时间多项式，在雷达静默期间，利用该组时间多项式估计目标的运动状态，辅助红外传感器对目标进行跟踪。文献［10］在极坐标系下，利用singer 模型对目标的距离、方位、俯仰分别进行跟踪，利用距离预测协方差和预定门限比较来确定雷达是否辐射。文献［11－14］利用交互多模型对目标进行跟踪，将预测协方差矩阵对角线上对应的x－y－z 方向的误差转换到极坐标系下的距离、方位、俯仰对应的误差，再分别与预定门限进行比较，任一个参数超过门限雷达就辐射。

本文研究了给定辐射时间限制下的雷达辐射规划问题，建立了雷达辐射最优规划模型，得出了最优规划准则。基于该准则，提出一种基于协方差的雷达实时辐射控制方法，并比较了不同辐射控制参数情况下雷达辐射时间，得出了一些有意义的结论。

1 问题描述

现代战场环境下，为了保证雷达的隐蔽性，雷达辐射时间需要进行控制。在给定一段时间内雷达辐射次数的情况下，对雷达辐射时机进行优化控制，可以提高目标状态的估计精度。假设目标跟踪过程在(0，T］时间段内进行，在该时间段内，限定雷达辐射次数为N 次，现要将这N 次雷达辐射时机点规划到(0，T］时间区间内，使得目标状态估计精度最高。假设目标匀速运动，运动模型为

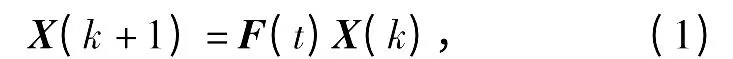
式中:X(k)为状态向量;F(t)为状态转移矩阵，其中，t 表示两个雷达辐射时机点时间间隔。

文献［5］提出雷达辐射控制最简单的模型是等间隔辐射模式，即将N 辐射时机点等间隔的分布在(0，T］时间区间内。研究发现，等间隔辐射并不是最优的辐射规划。那么，如何在(0，T］时间区间内规划N 次雷达辐射呢?本文建立辐射限制下的雷达辐射时机规划模型，理论推导出了最优规划准则。

2 雷达辐射时机最优规划

2.1 规划模型及推导

假设雷达跟踪目标的整个过程在(0，T］时间段内进行，限定该段时间段内雷达辐射次数为N.雷达辐射点分别是T1、T2、…、Tn－1、Tn.易知，要使得跟踪末端目标状态估计精度最高，跟踪末端雷达需要辐射，即Tn=T 时雷达需要辐射。雷达辐射规划示意图如图1所示。

图1 雷达辐射时机规划示意图Fig.1 Radar radiation timing scheme sketch map

假设采用Kalman 滤波对目标状态进行估计，由于目标状态估计误差协方差反映了目标状态估计误差的大小，因此辐射时机规划的优化目标函数f 可以取跟踪末端Tn处估计误差协方差的迹，即

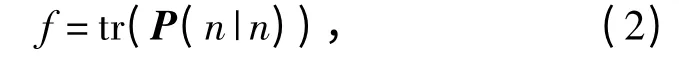
式中，P(n|n)为跟踪末端点Tn的状态估计误差协方差。

上述规划问题可以描述为一个动态规划问题。先假设给定辐射时机点Tn－2、Tn，规划Tn－1的位置，使得Tn点处目标状态估计误差协方差的迹tr(P(n|n))最小。得到Tn－1的位置后，再假设给定了Tn－1、Tn－3，规划Tn－2的位置，使得Tn－1点处目标状态估计误差协方差的迹tr(P(n－1|n－1))最小。依次类推，就可以得到整个时间段内雷达辐射点的规划。现在，假设已知T1、T2、…、Tn－1、Tn点中任意两点Ti－2、Ti(i∈(3，n］)的位置来规划Ti－1位置。

由于规划的优化目标函数f 等于跟踪末端Tn处目标状态估计误差协方差的迹，因此规划问题转化为已知Ti－2，Ti点位置和Ti－2点处状态估计误差协方差P(i－2|i－2)，规划Ti－1的位置，使得目标函数f=tr(P(i|i))值最小。这里不妨取x 方向上的规划来进行分析。

令

式中:ti=Ti－1－Ti;ti－1=Ti－2－Ti－1.

令目标x 方向量测误差为

量测矩阵H 为

假设Ti－2处目标状态估计误差协方差为

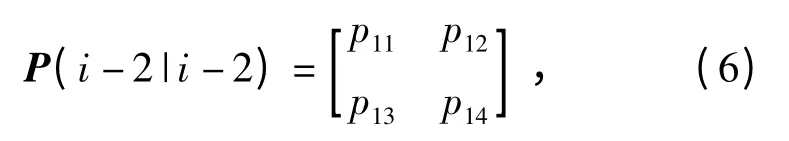
式中，p12=p13，且p11＞0，p12＞0，p13＞0，p14＞0.

令p11=ασ2x，p12=βσ2x，p22=γσ2x，其中α、β、γ 为常数，且α ＞0、β ＞0，γ ＞0.

那么

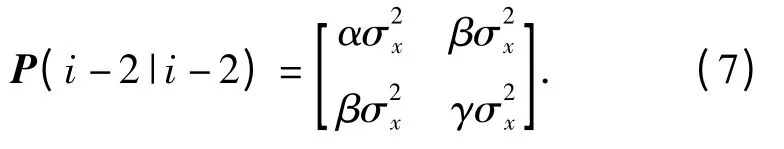
假设过程噪声为0，Ti－1处的预测误差协方差为

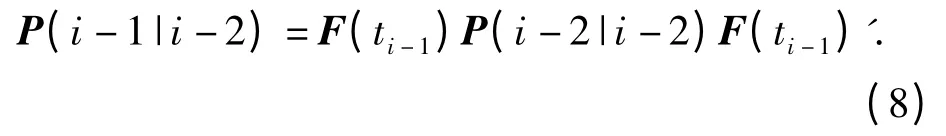
Ti－1处的估计误差协方差［15］为

Ti处的预测误差协方差为

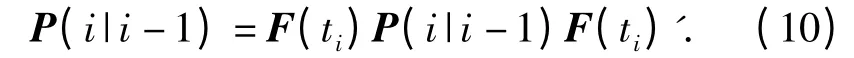
将ti－1=T－ti，带入式(10)可得

Ti处的估计误差协方差［15］为

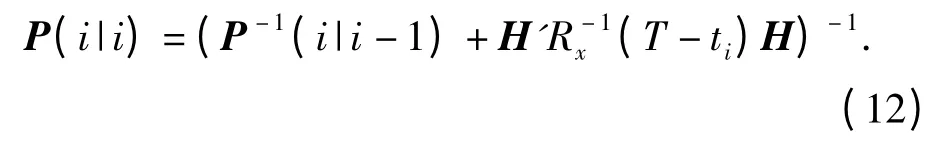
规划的优化目标函数为

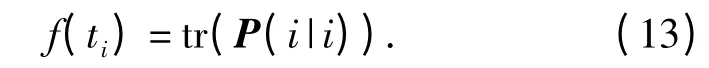
将等式(7)、式(8)、式(9)、式(10)、式(12)、式(13)逐步迭代可得

令

由柯西－许瓦兹不等式可知:

那么，f1(ti)表示开口向上，对称轴位于ti=－ β/γ处的抛物线，显然ti∈(0，T］时，f1(ti)函数值单调增加。f2(ti)表示开口向上，对称轴位于ti=T 处的抛物线，显然ti∈(0，T］时，f2(ti)函数值单调递减，且f2(ti)＞0.由式(14)可知，f(ti)＞0.所以f(ti)在ti∈(0，T)内是单调减少的，即当ti→T 时，f(ti)取极小值。

以上分析表明，在(Ti－2，Ti)内规划Ti－1的位置，Ti－1越靠近Ti，估计的误差越小;同理，在(Ti－3，Ti－1)中规划Ti－2的位置，Ti－2越靠近Ti－1，估计误差越小，依次类推。所以T1、T2、…、Tn－1、Tn在(0，T］内的最优化规划准则是:N 个辐射时机点相隔越近且越接近时间终点Tn，Tn处的估计误差越小。

2.2 模型验证

下面用迭代寻优的方法验证以上推导。假设雷达跟踪过程中辐射间隔最小单位为1 s，雷达辐射时机点正好在整数上。寻找最优辐射时机点依照下面步骤:

1)令常数M=∞;

2)利用循环嵌套(N 个辐射点就有N－1 个循环)，取雷达辐射时间分别为t1=1～(Tn－1)，t2=1～(Tn－1－t1)，…，tn－1=1～(Tn－1－t1－t2－，…，tn－2)，tn=Tn－1－t1－t2－，…，－tn－1;

3)得到一组雷达辐射点t1，t2，t3，…，tn，逐步迭代，计算得出tn点处的状态估计误差协方差，如果tr(P(n|n))＜M，则令M = tr(P(n|n))，Tmin(P)=［t1，t2，t3，…，tn］，返回第2)步;否则直接返回第2)步;

4)如果所有的可能辐射时机点都取完，即迭代到t1=Tn－n +1，t2=1，t3=1，…，tn=1 时，取出M和Tmin(P)，Tmin(P)即为雷达最优辐射规划分布点，M即为最优规划的函数值。

下面分别取规划总时间T=20 s，40 s，60 s，辐射次数N=2，5，10 时辐射规划的最优时机分布情况。

表1 不同跟踪时间和辐射次数下的辐射规划情况Tab.1 Radiation planning situation under different tracking time and radiation time

由表1可以看出，对于一段时间内给定辐射次数的最优规划分布点，集中分布在时间终点一端，证明了理论推导准则的正确性。在进行雷达辐射控制时，可以适当的增加辐射间隔时间，增加每次辐射的次数，这样会使得跟踪精度更高。由于结论是在过程噪声为0 的情况下得到的，考虑到实际情况中的过程噪声、目标机动、滤波算法非线性等因素的影响，每次辐射间隔不宜过大，那样可能导致滤波发散。

3 基于协方差的雷达实时辐射控制

3.1 方法描述

由上节推导结论可知，一段时间内雷达辐射规划最优原则是雷达辐射时机点集中于时间终点一端(辐射间隔不易过大)，基于该准则，本文提出了一种基于协方差的雷达时实辐射控制方法。方法描述如下:

1)航迹起始，两点法(或三点法)滤波初始化，得到初始协方差P0.

2)雷达连续辐射一段时间，建立稳定的航迹后进入辐射控制阶段。

3)确定雷达下次开机的时间，具体步骤为:

a)设Tleft=Tmin，Tright=Tmax(Tmin、Tmax分别表示雷达最小和最大辐射间隔)，进入循环;

b)如果Tright－Tleft＜ε(ε 为一个较小的常数)，退出循环，得到下一雷达辐射时刻点T =Tleft或T =Tright，否则令Ttest=Tleft+［(Tright－Tleft)/2］;

c)利用滤波公式和T =Ttest计算预测误差协方差P(k+T|k);

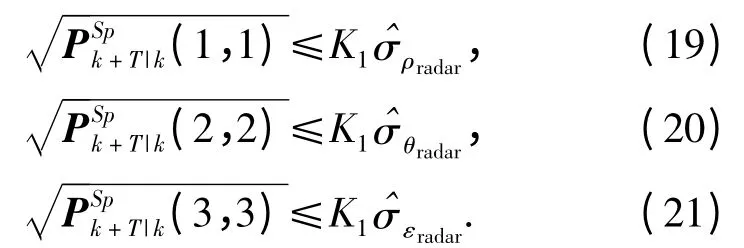
其中，K1为比例常数，其大小决定了预测协方差门限的大小。如果式(19)、式(20)、式(21)都成立，则Tleft=Ttest，否则Tright=Ttest，回到第b)步。

4)预定辐射时刻到，雷达连续辐射，利用滤波算法对目标进行跟踪，当目标位置误差小于预定门限时，即

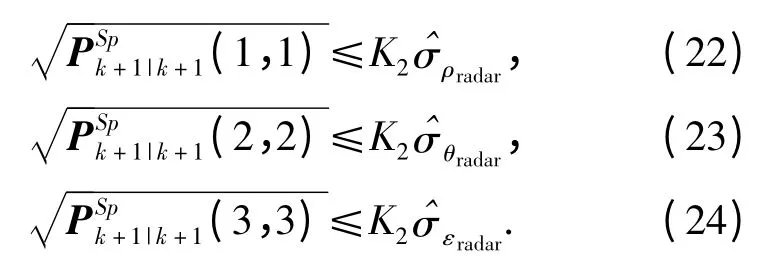
其中:K2为比例常数，如果式(22)、式(23)、式(24)都成立，雷达再次关机，返回第3)步计算下次雷达辐射时机点，否则连续辐射。

3.2 仿真

仿真环境1:我机地理坐标经度、纬度、高度为(37.0°，119°，10 000 m)，初始速度为(0，100 m/s，0)(表示纬度、经度、高度切线方向的速度);敌机地理坐标为(37.1°，119.5°，10 000 m)，初始速度都为(－200 m/s，100 m/s，0);我机和敌机都做匀速运动;仿真总时间110 s，雷达测距均方根误差为100 m，方位角均方根误差为0.2°，俯仰角均方根误差为0.2°，径向速度均方根误差为10 m.

仿真环境2:在仿真的时间内，敌机前1/8 时间段匀速运动，其后的1/4 时间段左转弯(转弯角速度为3 rad/s)，接着的1/4 时间段右转弯(转弯角速度为－3 rad/s)，最后1/8 时间段匀速运动，整个过程敌机运动呈蛇形。我机运动方式不变，其它仿真参数与环境1 相同。

仿真结果:

设置辐射门限K1=3，K2=0.6 时，对于仿真环境1，对应的敌我飞机飞行轨迹图如图2所示，雷达辐射时机图如图3所示，跟踪轨迹图如图4所示，跟踪总体距离误差图如图5所示。

图2 环境1 下敌我飞机飞行轨迹图Fig.2 Enemy and our aircraft flight trajectory under ensironment 1

图3 环境1 下雷达辐射时机图Fig.3 Radar radiation timing diagram under environment 1

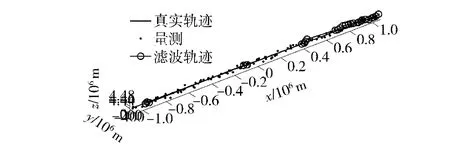
图4 环境1 下目标跟踪轨迹图Fig.4 Tracking trace under environment 1

对于仿真环境2，辐射控制的双门限不变，对应的敌我飞机飞行轨迹图如图6所示，雷达辐射时机图如图7所示，跟踪轨迹图如图8所示，跟踪总体距离误差图如图9所示。

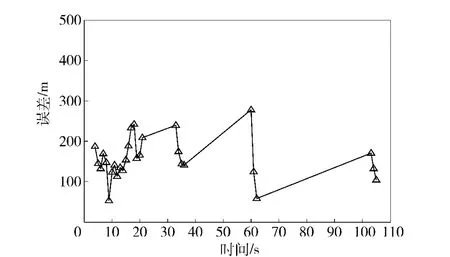
图5 环境1 下跟踪距离总体误差图Fig.5 Total distance tracking error diagram under lnvironment 1

图6 环境2 下敌我飞机飞行轨迹图Fig.6 Enemy and our aircraft flight trajectory under environment 2

图7 环境2 下雷达辐射时机图Fig.7 Radar radiation timing diagram under environment 2

从图2～图9可以看出:

1)提出的辐射控制方法能很好的根据预定精度门限要求控制雷达辐射，对匀速运动目标以及机动目标进行跟踪，形成一个反馈控制环路。

2)由于提出的控制方法采用跟踪误差和预测误差两个门限进行控制，既增加了雷达两次辐射之间的间隔时间，增强了雷达隐蔽性，同时又增加了跟踪精度，使得其能够达到预定精度。

图8 环境2 下目标跟踪轨迹图Fig.8 Tracking trace under environment 2

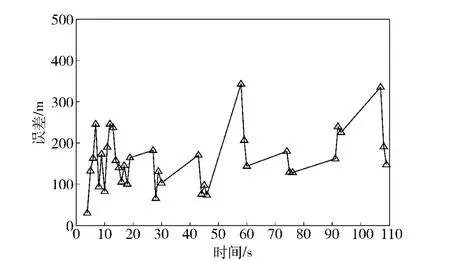
图9 环境2 下跟踪距离总体误差图Fig.9 Distance tracking error diagram under cnvironment 2

设置不同的门限，蒙特卡罗仿真100 次，比较对应的雷达开机时间如表2所示。其中对于匀速运动目标采用扩展卡尔曼滤波、蛇形机动目标采用交互多模型滤波进行跟踪。

表2 不同门限下的雷达开机时间比较Tab.2 Rdar radiation timing comparison of different threshold

从表2可以看出:

1)提出的辐射控制方法能在不同的控制参数下对匀速目标、机动目标进行正常的跟踪，对于相同的辐射控制门限，跟踪机动目标比跟踪匀速目标要求的雷达辐射次数多。

2)雷达辐射次数多少主要受预测协方差门限K1和滤波协方差门限K2的影响，实际应用的时候可以根据不同目标的跟踪需求选择控制门限，以达到控制雷达辐射的目的。

4 结论

本文研究了给定辐射时间限制下雷达辐射时机规划问题，建立了规划模型，理论推导出了雷达辐射时机最优规划准则。研究表明，给定辐射时间限制下，雷达辐射时机点越集中于时间终点，目标状态估计精度越高。基于该准则下，提出了一种实时雷达辐射控制方法，仿真实验证明了方法的合理性和有效性。研究结论还可以推广到单平台雷达与被动传感器以及多平台多传感器的协同管理与辐射控制，具有重要的军事意义和广阔的应用前景。

References)

［1］ Leibowicz I，Nicolas P，Ratton L.Radar/ESM tracking of constant velocity target:comparison of batch (MLE)and EKF performance［C］∥the Third International Conference on Information Fusion，2000:3－8.

［2］ Shin H J，Hong S M，Hong D H.Adaptive－update－rate target tracking for phased－array radar［J］.Radar，Sonar Navigation，1995，142(3):137－143.

［3］ 赵艳丽，刘剑，罗鹏飞.基于相控阵雷达的自适应采样目标跟踪算法［J］.现代雷达，2003，25(5):37－39.ZHAO Yan－li，LIU Jian，LUO Peng－fei.Adaptive sample target tracking algorithm for phased array radar［J］.Modern Radar，2003，25(5):37－39.(in Chinese)

［4］ 施龙飞，王雪松，肖顺平.基于新息范数的相控阵雷达自适应数据率跟踪［J］.舰船电子对抗，2005，28(5):45－47.SHI Long－fei，WANG Xue－song，XIAO Shun－ping.Adaptive data rate tracking of phased－array radar based on residue norm［J］.Shipboard Electronic Warfare，2005，28(5):45－47.(in Chinese)

［5］ 钟晓军，王国宏.异类多传感器系统中基于跟踪质量的辐射控制研究［J］.现代雷达，2004，26(2):18－21.ZHONG Xiao－Jun，WANG Guo－hong.A study on radiation control based on the tracking quality in heterogeneous sensors system［J］.Modern Radar，2004，26(2):18－21.(in Chinese)

［6］ LI A P，JING Z L，HU S Q.UKF－based multi－sensor passive tracking with active assistance［J］.Journal of Systems Engineering and Electronics，2006，17(2):245－250.

［7］ DOU L H，YANG G S.Synergy decision for radar and IRST data fusion［J］.Journal of Beijing Institute of Technology［J］.2002，11(3):229－231.

［8］ HU S Q，JING Z L.Sensor management in RADAR/ IRST track fusion［C］∥Proceedings of SPIE，Bellingham，2004，5430:173－181.

［9］ 李安平，敬忠良，胡士强.基于有源辅助的被动跟踪系统［J］.上海交通大学学报，2005，39(12):2048－2051.LI An－ping，JING Zhong－liang，HU Shi－qiang.The passive tracking system with active assistance［J］.Journal of Shanghai Jiaotong Universitty，2005，39(12):2048－2051.(in Chinese)

［10］ Baudo O，Rattonl L.Radar scheduling with emission constraints［C］∥Proceedings of SPIE，2002，4714:153－156.

［11］ 程咏梅，潘泉，张洪才.红外/雷达传感器协同跟踪算法研究［J］.火力与指挥控制，2001，26 (3):20－23.CHEN Yong－mei，PANG Quan，ZHANG Hong－cai.Study on infrared and radar sensor synergistic tracking algorithm［J］.Fire Control and Command Control，2001，26(3):20－23.(in Chinese)

［12］ Watson G A，Blair W D.Revisit calculation and waveform control for a multifunction radar［C］∥Proceedings of 32nd IEEE Conference on Decision and Control，San Antonio，1993，12:448－453.

［13］ Watson G A，Blair W D.Tracking maneuvering targets with multiple sensors using the interacting multiple model algorithm［C］∥Proceedings of SPIE，1954:438－449.

［14］ Watson G A，Blair W D，Rice T R.Enhanced electronically scanned array resource management through multisensor integration［C］∥Proceedings of SPIE，3163:329－340.

［15］ 何友，王国宏，陆大纟金，等.多传感器信息融合及应用［M］.电子工业出版社，2007:14－15.HE You，WANG Guo－hong，LU Da－jin，et al.Multisensor information fusion and its application［M］.Beijing:Electronic Industry Press，2007:14－15.(in Chinese)