对抗雷达网最优电子战布阵研究
2012-02-22陈中起于雷鲁艺周中良
陈中起,于雷,鲁艺,周中良
(空军工程大学 工程学院,陕西 西安710038)
0 引言
现代战场环境中,敌方雷达为有效抗击所面临的“四大威胁”[1],常采用先进的组网技术[2],使雷达网具有很强的“四抗”能力[1]。因此,即使是隐身性能比较好的现代战斗机也很难实现安全突防,常需要借助于支援干扰对敌雷达网实施有效地压制。当前国内外对电子干扰的研究主要侧重于干扰压制效果及干扰机作战效能等方面[3],对干扰机和攻击机的协同突击作战的研究相对较少,而且研究往往缺乏明确的衡量指标,从而使结果很难应用于实战中去。文献[1]重点考虑了干扰机或干扰机编队作环形机动时,干扰机的运动给干扰效果造成的影响,提出了“干扰过渡区”的概念;文献[4]在干扰机布阵方案已知的情况下,研究了对抗敌雷达网的压制效果,在此基础上进行航迹规划;文献[5]给出了干扰机布阵的概念,重点对直线布阵和扇形布阵两种形式进行了研究;文献[6]以协同干扰功率最大为目标,给出了编队协同有源压制性干扰作战使用的一般原则。
而研究干扰机协同攻击机进行突击规划,首先需解决规划空间的生成问题,而攻击机执行不同的突击作战任务、所具有的不同机动飞行性能以及不同的编队组成等对规划空间都有不同的要求。
基于此,本文首先提出了安全走廊的概念,以其宽度作为干扰效果的衡量指标,重点研究为获得特定宽度安全走廊,对抗敌雷达网干扰机的最优布阵问题,这也是进行突击航迹规划的基础;为此提出了一种基于数学形态学的安全走廊宽度的计算方法;根据安全走廊宽度要求,通过遗传算法解决了多部干扰机的最优布阵问题,最后进行了实例仿真验证。
1 基本概念及电子战模型
1.1 雷达探测范围
本文中的雷达探测范围是指对于特定的雷达,特定的目标雷达散射截面,由于地形遮蔽影响,在雷达最大作用范围内,在各个方位方向上,雷达视线被山地所遮挡形成,其边界是由雷达视线与山体表面所成仰角最大位置处点组成。需说明的是本文重点研究的是为获得特定宽度安全走廊,干扰机的最优布阵问题,因此暂未考虑攻击机RCS 的动态变化对探测范围的影响,文中将其设为定值σ=1 m2.

图1 φ 方位方向雷达探测范围示意图Fig.1 Radar detecting range in φ azimuth
由图1知,ρh(φ)对应φ 方向探测范围远边界点,θmax为在最大探测范围内雷达视线与山体表面所成的最大仰角。
1.2 安全走廊
安全走廊是指攻击机可以安全飞行的航路带,它构成了攻击机最优航迹规划的搜索空间。主要参数有走廊宽度、走廊高度,其中走廊宽度是指整条走廊最窄处的宽度。
本文中基于雷达探测范围的安全走廊是指在某一高度范围内不被敌雷达网探测到的一条相对安全的航路带。
1.3 复杂电子压制模型
1)单部干扰机电子压制模型
由目标回波信号功率[3]及噪声功率模型可得雷达接收端信噪比模型如下

干扰机干扰信号进入雷达接收机输入端的功率为

于是可得综合噪声和干扰信号的综合信噪比模型如下
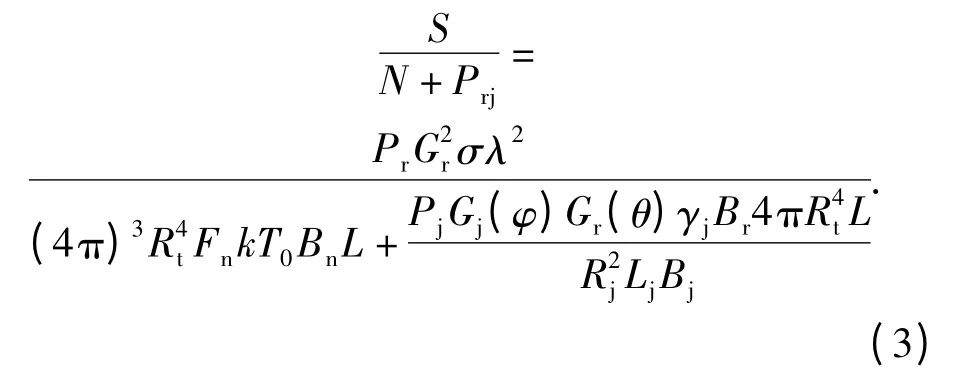
由雷达最小压制系数K 可得单部干扰机实施电子压制后雷达最大探测距离为
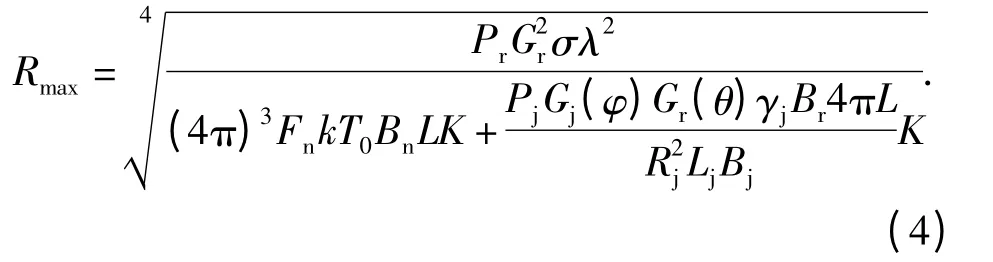
2)多部干扰机电子压制模型
对于多部干扰机的情况采用信号叠加原理,如上所述,可得电子压制后雷达最大探测距离为

式(1)~式(5)中,(S/N)0min为雷达最小可检测信噪比;Pr、Pj分别为雷达和干扰机发射功率;Gr、Gj分别为雷达和干扰机发射增益;σ 为目标雷达散射面积;λ 为雷达波长;Rt为雷达目标间距离;Rj为干扰机至雷达的距离;γj为干扰机极化损失;Fn为噪声系数;k为波尔茨曼常数;T0为工作温度;Bn、Br、Bj分别为噪声信号、雷达接收机和干扰信号带宽;L、Lj分别为雷达和干扰机综合损耗因子;Gj(φ)为干扰机天线在雷达方向增益;Gr(θ)为雷达天线在干扰机方向的增益;Pji、Rji、Lji、Bji、γji、Gji(φi)分别为第i 部干扰机发射功率、与被压制雷达间距离、综合损耗因子、信号带宽、极化损失及天线在被压制雷达方向增益;这里假设雷达发射、接收共天线。
2 基于数学形态学的安全走廊宽度的计算
2.1 数学形态学
数学形态学(Mathematical Morphology)诞生于1964年。腐蚀(Erosion)和膨胀(Dilation)是其两个基本运算。
1)数学形态学的腐蚀运算
腐蚀运算机理如图2所示,在二值形态学中,模板B 对图形A 的腐蚀记为A⊖B,定义为

如果原点在结构元素内部,那么腐蚀具有收缩输入图像的作用。
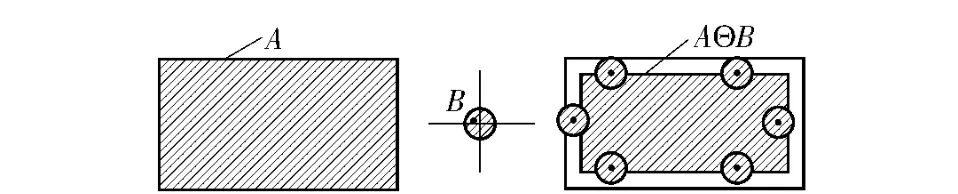
图2 腐蚀运算机理Fig.2 Erosion operating mechanism
2)数学形态学的膨胀运算
膨胀是腐蚀的对偶运算,其运算机理如图3所示,可以通过对补集的腐蚀来定义,A 被B 膨胀表示为A⊕B,定义为

由图3知,膨胀具有扩大图像作用。

图3 膨胀运算机理Fig.3 Dilation operating mechanism
2.2 安全走廊宽度的计算
由安全走廊的定义可知,安全走廊是位于雷达网之间,不被雷达探测的区域。它限制了攻击机航迹规划范围[7-9],是规划攻击机最优航迹的前提;如前所述,执行任务不同,如单机或多机协同航迹规划[10],对安全走廊的宽度会有不同的要求;此外,由于攻击机导航系统精度或先验信息不准确等因素的影响,在确定航迹时,保持足够的安全走廊宽度更有实际意义。如果安全走廊的宽度不够大或未能达到预定要求,可能迫使攻击机穿越所谓的“台风眼”区域[11]。因此,研究给定条件下安全走廊宽度的计算具有重要的实际意义。
然而,由于受地形影响,雷达网的探测范围是不规则图形,如图4所示。若直接使用几何法计算压制后的走廊宽度,不仅不易建立准确的数学模型,而且计算量将会很大;但若将雷达网探测范围转化为二值图像,选定结构元素,不断对图像做膨胀运算,同时进行图像连通性判断,获取图像中图形元素的数量,进而判断是否形成安全走廊并求解走廊宽度,可避开对雷达探测范围具体形状的建模,具体计算流程如图5所示。

图4 雷达网探测范围示意图Fig.4 Radar net detecting range diagram

图5 安全走廊计算过程Fig.5 Safe corridor calculating process
3 基于遗传算法的最优电子战布阵
3.1 问题描述
在现代复杂电子环境中,由于敌雷达网通过布阵时具备“四抗”能力,因此单部干扰机很难实现对敌雷达网有效压制,形成一定宽度的安全走廊。若派出多部干扰机,单凭经验很难充分发挥干扰机的效能,并使压制结果达到预定要求。
针对整个战场环境,暂不考虑攻击机和干扰机间的战术协同,根据战场威胁情况,研究确定多部干扰机的最优布阵问题,目的是要求充分考虑干扰机自身的安全因素,对战场威胁以最有效的压制,并满足特定安全走廊宽度要求,进而扩大突防航迹搜索范围,为攻击机的最优航迹搜索做准备。
3.2 电子战最优布阵模型
基于3.1 节问题描述,考虑敌雷达网布阵如图6所示,为保证干扰效果电子干扰机布阵范围要求在外边界之内,同时要在各部雷达探测范围之外,要求干扰机压制后的安全走廊宽度不得小于某一值,且越宽越好,于是有如下电子战最优布阵模型:

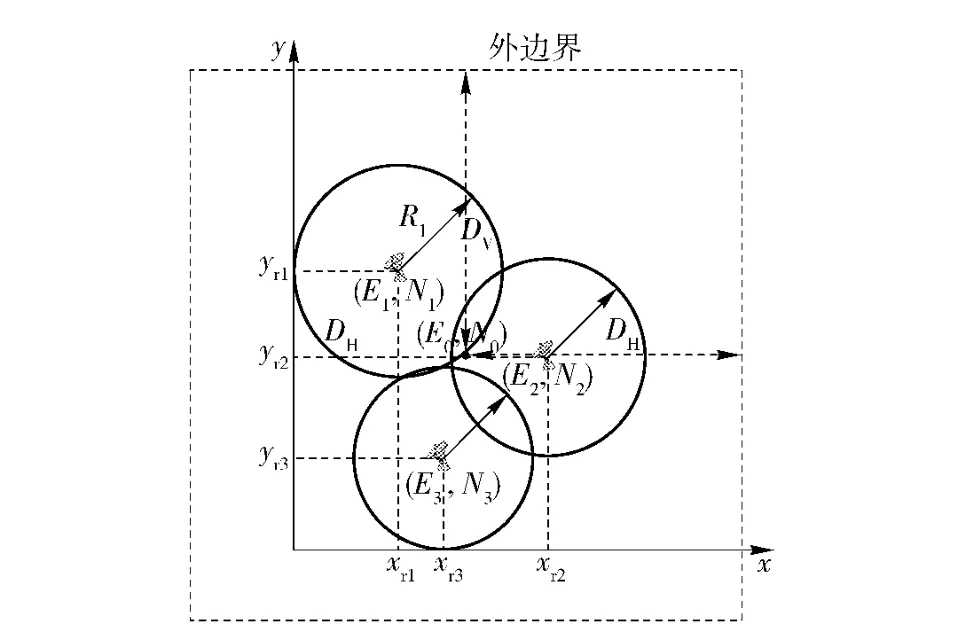
图6 雷达分布示意图Fig.6 Radar distributing diagram
3.3 基于遗传算法的最优电子战布阵的实现
遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法。现己被证明是一种有效的解决复杂问题的方法,由于它不受搜索空间的限制性假设的约束,不必要求诸如连续性、导数存在和单峰等假设,采用多点同时进行搜索,每次迭代通过交换和变异运算产生新的个体,不断扩大搜索范围,从而有效避免了陷入局部最优解。在进化过程中,每一代运算都是针对一组个体同时进行,而不只是针对单个个体,因此遗传算法便于实施并行计算,大大提高了进化算法的速度。基于此,本文采用该算法来实现多干扰机对雷达网压制时布阵寻优问题,具体实现如下。
1)适应度函数
适应度函数取式(8)中的目标函数,即,fitness=F.
2)编码方式
采用二进制编码方式,为提高计算精度,各干扰机位置采用经纬度坐标表示,且经度和纬度的编码长度均取L=10,编码规则如图7所示。
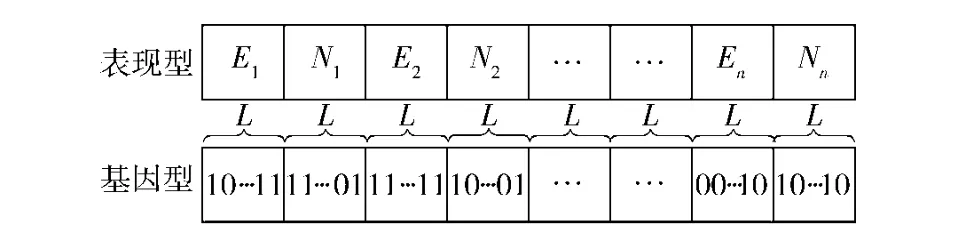
图7 编码方式Fig.7 Encoding mode
3)自适应交叉和变异概率计算模型

式中,F 表示个体适应度值大小,Fmax为设定的最大适应度值;Favg为本代中平均适应度值;Pc0为设定的交叉概率;Pm0为设定的变异概率。
结合第2 节计算安全走廊宽度的方法,通过该算法可搜索出满足最小安全走廊宽度限制且走廊数最多的干扰机布阵方案。
4 仿真分析
假设某次攻击任务中,敌方雷达网由3 部雷达组成,经纬度坐标分别是(EX1,NY1),(EX2,NY2),(EX3,NY3),架设高度均为50 m,为了获得至少10 km宽度的安全走廊,以备实现后续的突防航迹规划任务,我方派遣2 架电子干扰机对敌雷达网进行压制性干扰,且任意指定干扰机1 主瓣对准雷达2,干扰机2 主瓣对准雷达3,敌雷达和我干扰机性能参数如下:

表1 雷达网中各雷达的性能参数Tab.1 Radar parameters in radar net
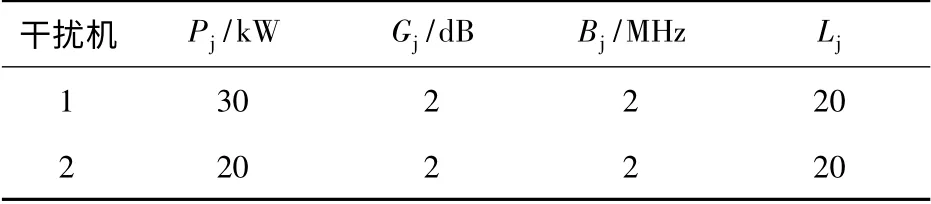
表2 干扰机参数列表Tab.2 Jamming plane parameters
设定σ=1 m2,干扰机高度为4 km,且假定干扰机在规定位置周围作圆周机动,各部雷达的有效压制系数K=5.于是结合数字地图处理技术可得敌雷达网受地形影响后的探测范围及二值化后的情形分别如图4、图8所示。由图4、图8可知,各部雷达探测范围重叠,具有一定的“四抗”能力,我突防飞机很难不被发现地突防过去。采用本文所提干扰机最优布阵算法在上下、左右各6 个经纬度范围内搜索预定安全走廊宽度的最优布阵方案。
仿真1:取λ1=0.8,λ2=0.2,初始种群设为80,进化代数100,可得最终进化曲线如图9,两部干扰机的最优布阵方案和压制后的结果如图10、图11所示,即两部干扰机应布置如图10 中圆点所示,得安全走廊宽度d=36 km.

图8 雷达网二值图像Fig.8 The binary image of radar net

图9 遗传算法进化曲线Fig.9 Evolution curve of genetic algorithm
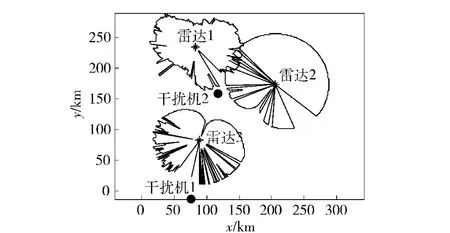
图10 λ1 =0.8,λ2 =0.2 最优布阵方案及压制结果Fig.10 The best distributing plan and jamming result when λ1 =0.8,λ2 =0.2

图11 λ1 =0.8,λ2 =0.2 压制结果二值图像Fig.11 The binary image of jamming result when λ1 =0.8,λ2 =0.2
仿真2:取λ1=0.5,λ2=0.5,其余参数不变再寻优一次,可得到干扰机布阵方案及压制后结果如图12、图13 所示,此时,d=25 km.由图10、图12可知,所得最优方案均达到了要求的压制效果,形成了满足预定宽度的安全走廊。若属性权重侧重于压制效果而不是干扰机安全,得到的布阵方案如图10 所示,干扰机2 距离威胁中心很近,但形成的安全走廊宽度很宽,反之若同时注重干扰机安全,则得到结果如图12 所示,两部干扰机均远离威胁中心,但压制后的安全走廊宽度不如图10 宽。
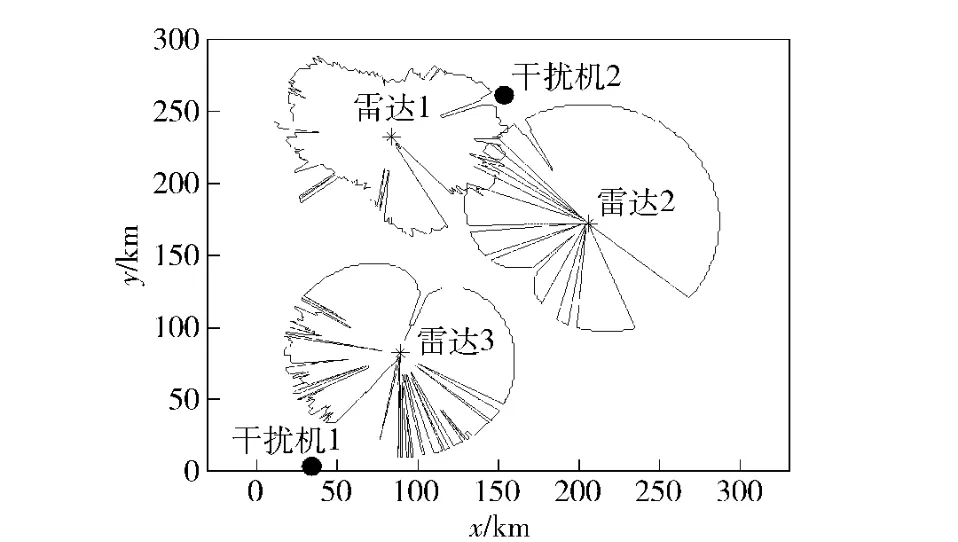
图12 λ1 =0.5,λ2 =0.5 最优布阵方案及压制结果Fig.12 The best distributing plan and jamming result when λ1 =0.5,λ2 =0.5

图13 λ1 =0.5,λ2 =0.5 压制结果二值图像Fig.13 The binary image of jamming result when λ1 =0.5,λ2 =0.5
5 结论
为有效压制敌雷达网扩大突击规划搜索空间,通过电子干扰机最优布阵策略,得到特定安全走廊宽度的压制效果,是突击规划的前提和基础,很有作战实用意义,本文的主要结论有:
1)给出了实际地形中雷达探测范围及安全走廊的概念,为干扰效果建立了明确的衡量指标;
2)通过引入数学形态学方法,建立了对抗雷达网获取要求安全走廊宽度的计算方法,有效地避开了对雷达网复杂外形的建模;
3)设计出了基于数学形态学的遗传算法求解方案,可快速计算出真实地形情况下,既充分考虑走廊宽度要求,又考虑干扰机安全的最优电子战布阵方案。最后的仿真结果表明了所提方法对问题解决的有效性。
References)
[1] 申绪涧,王国玉,汪连栋,等.电子干扰飞机对抗警戒雷达组网系统效果评估[J].系统仿真学报,2008,20(4):997-1000.SHEN Xu-jian,WANG Guo-yu,WAGN Lian-dong,et al.Effect evaluation for electronic jamming aircraft against netted surveillance radars[J].Journal of System Simulation,2008,20(4):997-1000.(in Chinese)
[2] 王中杰,李侠,周启明,等.基于多约束条件遗传算法的雷达网优化部署[J].系统工程与电子技术,2008,30(2):265-268.WANG Zhong-jie,LI Xia,ZHOU Qi-ming,et al.Optimal deployment of radar network based on multi-constrained GA[J].Systems Engineering and Electronics,2008,30(2):265-268.(in Chinese)
[3] 陈晋鹏,王红军.支援干扰条件下压制区域模型的建立与仿真[J].电子对抗,2008,3:24-28.CHEN Jin-peng,WANG Hong-jun.Modeling and simulation of suppressing area from stand-off Jamming[J].Electronic Warfare,2008,3:24-28.(in Chinese)
[4] 史和生,李丹,赵宗贵,等.电子干扰对低可观测飞行器飞行路径规划的影响[J].南京航空航天大学学报,2007,39(2):154-158.SHI He-sheng,LI Dan,ZHAO Zong-gui,et al.Electronic jamming exercises influence on flight path planning of low observation aircraft[J].Journal of Nanjing University of Aeronautics & Astronautics,2007,39(2):154-158.(in Chinese)
[5] 邢美丽,肖军鹏.复杂电磁环境下协同干扰技术研究[J].遥测遥控,2010,31(4):29-32.XING Mei-li,XIAO Jun-peng.Research on cooperative jamming in complex electromagnetic environment[J].Journal of Telemetry,Tracking and Command,2010,31(4):29-32.(in Chinese)
[6] 隋江波,吴玲,严亮.编队协同有源压制干扰作战使用研究[J].现代防御技术,2009,37(5):104-109.SUI Jiang-bo,WU Ling,YAN Liang.Operational application method of fleet active barrage jamming based on collaboration[J].Modern Defence Technology,2009,37(5):104-109.(in Chinese)
[7] Frank W Moore.Radar cross-section reduction via route planning and intelligent control[J].IEEE Transactions on Control Systems Technology,2002,10(5):696-700.
[8] Misovec K,Inanc T.Low-observable nonlinear trajectory generation for unmanned air vehicles[J].IEEE Conference on Decision and Control,2003,12:3103-3110.
[9] Tamer Inanc,Kathy Misovec,Richard M Murray.Nonlinear trajectory generation for unmanned air vehicles with multiple radars[J].IEEE Conference on Decision and Control,2004,12:3817-3822.
[10] Atif Chaudhry,Kathy Misovec,Raffaello D Andrea.Low observability path planning for an unmanned air vehicle using mixed integer linear programming[J].IEEE Conference on Decision and Control,2004,4:1-8.
[11] 闵昌万,袁建平.航迹规划中安全走廊及参考轨迹的确定[J].飞行力学,1999,17(2):13-18.MIN Chang-wan,YUAN Jian-ping.The determination of safe corridor and reference path in route planning[J].Flight Dynamics,1999,17(2):13-18.(in Chinese)
