基于贝叶斯估计的漏磁缺陷轮廓重构方法研究

苑希超，王长龙，王建斌

(军械工程学院 电气工程系，河北 石家庄050003)

0 引言

武器装备中很多机件都是由铁磁材料制成的，如火炮炮管等，对这些装备和部件进行无损检测具有十分重要的意义。漏磁检测是铁磁材料的常用无损检测方法之一［1］，具有原理简单、在线检测能力强、不受材料表面油污及其他非导磁覆盖物影响等优点。漏磁检测包括正演和反演两个方面，漏磁缺陷轮廓重构是指由检测到的漏磁信号重构缺陷轮廓及参数，是实现漏磁反演的关键［2］。反演问题是不适定的，目前国内外对漏磁反演问题的研究主要有优化法等［3－5］，神经网络法［6－8］。优化法需要建立一个目标函数，通过各种算法使目标函数的值最小，在优化过程中需要根据正问题的模型反复迭代计算，因此计算量很大;神经网络具有非线性映射和自学习能力，能实现输入漏磁信号和输出裂纹形状非线性关系的逼近。但神经网络法对噪声敏感。

粒子滤波是一种基于蒙特卡罗和递推贝叶斯估计的算法［9－10］，它通过在状态空间中寻找一系列随机样本来近似后验概率密度分布。粒子滤波器可以实现任意状态的估计，尤其在非线性非高斯状态的估计中估计性能远优于扩展卡尔曼滤波器和无迹卡尔曼滤波器。将反演问题描述为基于状态和观测方程的典型的离散时间跟踪问题，建立缺陷轮廓与漏磁信号的状态空间模型，采用粒子滤波算法解决漏磁缺陷重构问题。

1 漏磁缺陷重构模型

漏磁检测的缺陷重构，是由给定的漏磁场数据求出铁磁材料中是否存在缺陷、缺陷的位置和形状，从而实现缺陷检测的可视化。漏磁检测系统是一个非线性系统，而现实中的噪声也都是非高斯的。因此，要建立更一般的、更符合实际的模型，即非线性、非高斯模型。

将漏磁检测模型用状态空间表示，如图1所示。

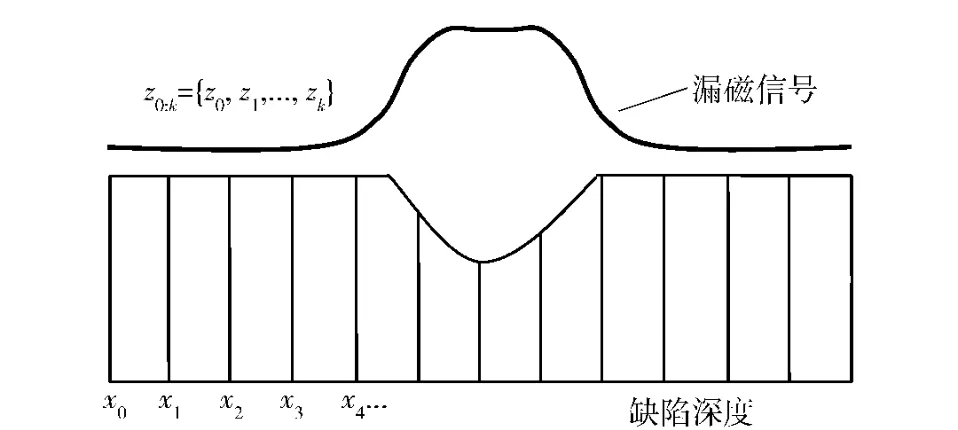
图1 漏磁检测的状态空间模型表示Fig.1 The state space model of MFL testing

以缺陷深度序列为系统的状态序列x0:k={x0，x1，…，xk}，量测序列为在对应状态序列位置检测到的漏磁信号切向分量z0:k={z0，z1，…，zk}，k 为序列标号，xk表示k 点的缺陷深度量，zk表示k 点的漏磁信号测量值。漏磁缺陷二维轮廓重构过程如图2所示，通过粒子滤波模型用漏磁信号进行状态估计到缺陷二维轮廓。

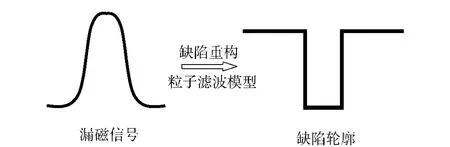
图2 漏磁缺陷二维轮廓重构Fig.2 Reconstruction of 2－D MFL defect profile

漏磁缺陷信息重构包括缺陷几何参数和缺陷位置等的重构，缺陷位置一般可由检测距离来确定。在这里重点研究由缺陷产生的漏磁场信号重构缺陷的几何轮廓，即由漏磁信号得到缺陷轮廓。可以通过建立状态空间模型将重构过程描述为跟踪问题。

2 基于粒子滤波的缺陷重构方法

2.1 粒子滤波基本原理

粒子滤波是一种基于蒙特卡罗方法的贝叶斯滤波算法［9－10］。其基本思想是:通过寻找一组在状态空间中传播的随机样本(粒子)对概率密度函数进行近似，以样本均值代替积分运算，从而获得状态最小方差估计的过程。对于一个动态系统，其状态空间模型表示如下:

状态方程为

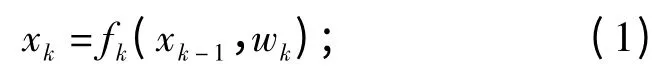
量测方程为

其中，wk为k 点独立同分布的过程噪声，vk为k 点独立同分布的量测噪声，非线性映射f 和h 代表模型的状态转移函数和量测函数。

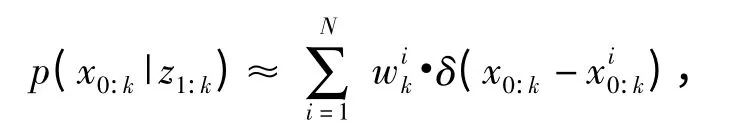
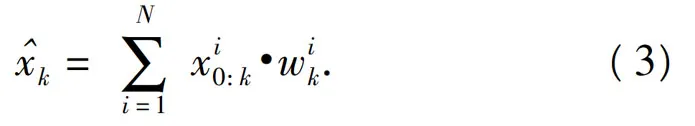
2.2 状态空间模型的建立

将缺陷深度序列和漏磁信号幅值序列用状态空间表示。采用概率模型作为系统的状态模型，k－1位置到k 位置的状态转移表示为

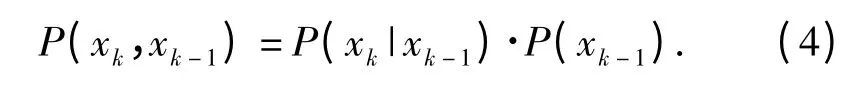
选择状态转移概率使当前缺陷深度的概率较大，而其他缺陷深度的概率较小。

观测模型是指状态xk与k 位置的测量值zk的关系，可由神经网络模型，数值计算模型或者多项式模型表示。但考虑到多项式模型计算量小且易于实现的优点，观测模型采用多项式模型表示。

2.3 实验数据组成

建立缺陷漏磁信号与缺陷特征的观测模型，需要有正确反映两者关系的样本。样本库包括实验数据与仿真数据。

取一长500 mm，内径为100 mm，壁厚8 mm 的1/8 管道圆弧样板作为试验试件，材料属性为X52钢，在试件内壁加工多个不同尺寸的人工裂纹缺陷。应用漏磁检测装置沿缺陷宽度方向对试件进行等间隔采样，并应用小波阈值消噪处理后得到实验数据。仿真数据的获得是基于有限元理论，对不同尺寸的矩形裂纹进行二维建模仿真，获取所需的样本数据。为了模拟真实的漏磁场信号，仿真样本中人为的加入了不同程度的噪声。

样本库共有30 组数据，其中6 组为实验数据，24 组为仿真数据。由于实验数据与仿真数据采样点数不一致，将其归一化为每组数据1 000 个样本点。裂纹宽度取值范围0.5～1.5 mm，深度取值范围15%～50%.

2.4 粒子滤波反演方法

根据缺陷样本库建立漏磁信号的观测模型，根据式(4)建立状态转移模型，采用粒子滤波方法进行二维缺陷轮廓重构。由式(3)可得到缺陷轮廓信息(状态估计)。粒子滤波重构流程如图3所示。

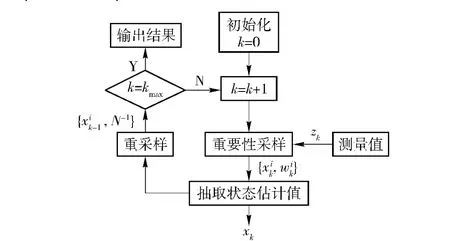
图3 粒子滤波算法流程图Fig.3 The flowchart of PF algorithm

3 重构结果及分析

采用粒子滤波方法进行重构分析。图4给出了不同缺陷尺寸下基于粒子滤波重构算法的反演结果。结果表明，该方法可以很好的完成缺陷的二维轮廓重构，且不需要对样本进行训练，反演速度快，是一种有效可行的缺陷重构方法。

粒子滤波算法不需要进行大量的迭代计算，计算量主要集中在解决粒子的退化问题上，而相关的一系列改进重采样算法有效地解决了该问题，进一步提高粒子滤波的计算速度［11－12］。因此，与优化法相比，粒子滤波算法计算速度快。

为进一步研究粒子滤波方法在不同信噪比下的反演效果，引入均方根误差(RMSE)作为评价指标

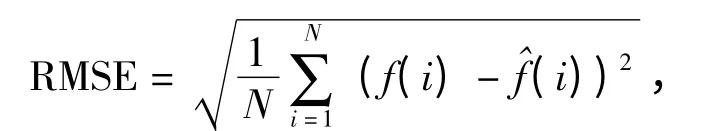
式中:f 为实际缺陷轮廓序列，f^ 为重构的缺陷轮廓序列，N 为序列的样本点数。分别采用常用的径向基函数神经网络(RBFNN)和粒子滤波发对不同信噪比下的漏磁信号就行了缺陷反演。表1给出了不同信噪比下采用径向基函数神经网络法和粒子滤波缺陷重构的均方根误差比较。如表中所示，采用神经网络法时，随着信噪比的降低，反演结果的均方误差明显增加;而采用粒子滤波法时，随着噪声信噪比水平的不同，反演结果的均方根误差增加不大，在存在较高噪声情况下也能完成缺陷的反演。图5给出其中信噪比分别为25，15 和5 时采用粒子滤波反演效果。

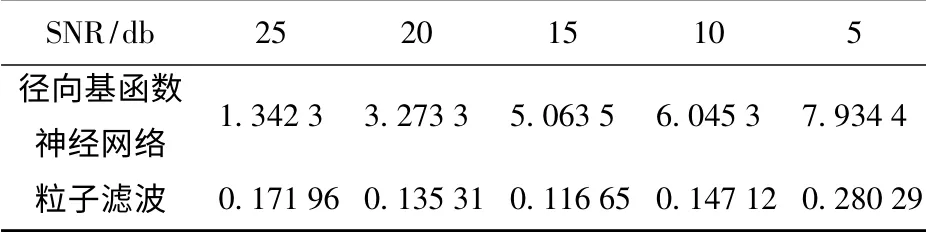
表1 不同信噪比(SNR)下的反演均方根误差比较Tab.1 The comparison of reconstruction RMSE

4 结论

将漏磁缺陷反演过程描述为典型的离散时间跟踪问题，提出一种基于递推贝叶斯估计方法的漏磁缺陷二维轮廓重构算法，采用粒子滤波算法对缺陷进行了二维轮廓重构。结果表明:基于粒子滤波的漏磁信号反演算法精度高，同时对噪声具有很强的鲁棒性，计算速度快，不需要大量的迭代计算，克服了优化法计算量大的不足，是一种有效可行的漏磁反演新方法。

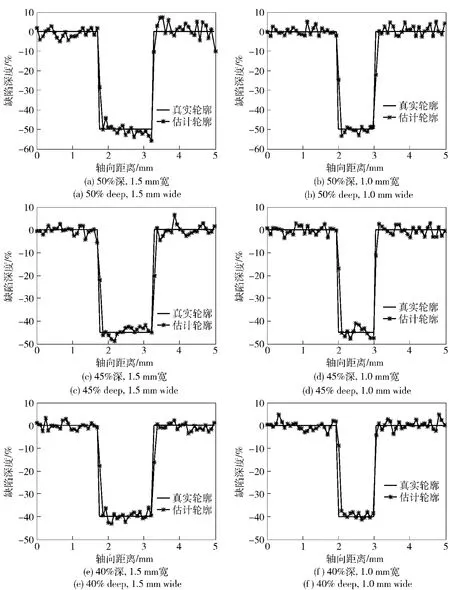
图4 两种重采样算法状态估计Fig.4 The state estimations of the two resampling algorithm

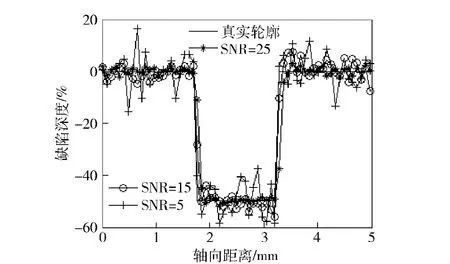
图5 不同噪声强度时的反演效果Fig.5 The pictorial diagram of the reconstruction performance with different noise level

References)

［1］ Snarskii A A，Zhenirovskyy M，Meinert D，et al.An integral equation model for the magnetic flux leakage method［J］.NDT ＆ E International，2010，43:343－347.

［2］ Ji Fengzhu，Wang Changlong，Zuo Xianzhang，et al.LS－SVMbased reconstruction of 3－D defect profile from magnetic flux leakage signals［J］.Insight，2007，49(9):516－520.

［3］ Ravan M，Amineh R K，Koziel S，et al.Sizing of 3－D arbitrary defects using magnetic flux leakage measurements［J］.IEEE Transactions on Magnetics，2010，46(4):1024－1033.

［4］ Amineh R K，Koziel S，Nikolova N K，et al.A space mapping methodology for defect characterization from magnetic flux leakage measurements［J］.IEEE Transactions on Magnetics，2008，44(8):2058－2065.

［5］ 刘美全，徐章遂，王建斌.基于磁偶极子能级分布的缺陷反演成像［J］.中国机械工程，2005，16(11):952－955.LIU Mei－quan，XU Zhang－sui，WANG Jian－bin.Inverse imaging for defects based on energy level of the magnetic dipole［J］.China Mechanical Engineering，2005，16(11):952－ 955.(in Chinese)

［6］ Carvalhoa A A，Rebelloa J M A，Sagrilo L V S.MFL signals and artificial neural networks applied to detection and classification of pipe weld defects［J］.NDT ＆ E International，2006，39:661－667.

［7］ 纪凤珠，王长龙，王瑾，等.基于稀疏化LS－SVM 的漏磁缺陷三维轮廓重构［J］.兵工学报，2008，29(5):592－595.JI Feng－zhu，WANG Chang－long，WANG Jin，et al.3－D defect profile reconstruction from magnetic flux leakage signals based on sparsity LS－SVM［J］.ACTA Armamentarii，2008，29(5):592－595.(in Chinese)

［8］ 韩文花，阙沛文，梁巍.改进的遗传局部搜索算法在漏磁逆问题中的应用研究［J］.上海交通大学学报，2007，41(5):751－754.HAN Wen－hua，QUE Pei－wen，LIANG Wei.The application of an improved genetic local search algorithm to MFL inverse problem［J］.Journal of Shanghai Jiao Tong University，2007，41(5):751－754.(in Chinese)

［9］ Djuric P M，Kotecha J H，ZHANG Jianqui，et al.Particle filtering［J］.IEEE Signal Processing，2003:19－38.

［10］ Arulampalam S，Maskell S，Gordon N，et al.A tutorial on particle filters for on－line non－linear/non－Gaussian Bayesian tracking［J］.IEEE Trans.Signal Process，2002，(50):174－189.

［11］ 王来雄，黄士坦.一种新的粒子滤波算法［J］.武汉大学学报(工学版)，2006，39(1):118－120.WANG Lai－xiong，HUANG Shi－tan.A novel particle filter algorithm［J］.Engineering Journal of Wuhan University，2006，39(1):118－120.(in Chinese)

［12］ 胡昭华，宋耀良.一种用于运动跟踪的加窗粒子滤波新算法研究［J］.南京理工大学学报，2007，31(3):337－341.HU Zhao－hua，SONG Yao－liang.Motjion tracking based on novel winding particle filter［J］.Journal of Nanjing University of Science and Technology，2007，31(3):337－341.(in Chinese)