一种新的混合智能粒子滤波算法在雷达机动目标跟踪中的应用

陈志敏，薄煜明，吴盘龙，陈沁欣

(南京理工大学 自动化学院，江苏 南京210094)

0 引言

雷达作为主动传感器的代表，由于其性能不受天气情况的影响，以及获得目标量测的优秀性能，至今仍在跟踪系统中起着重要的作用。在雷达目标跟踪系统中，测量噪声往往会受到闪烁噪声的干扰［1］，由于闪烁噪声具有显著的非高斯分布特性，而常规的滤波算法大多是在Kalman 理论框架下的方法，在闪烁噪声较大的情况下难以得到精确的结果。粒子滤波(PF)是一种基于蒙特卡罗思想的滤波方法，由于其在处理非高斯非线性时变系统的参数估计和状态滤波问题方面有独到的优势，因此在闪烁噪声下机动目标的跟踪中得到重视［2］。但是标准粒子滤波算法中存在着计算量过大和精度不高的问题，并且粒子匮乏现象不可避免，这个Doucet［3］和Kong［4］都已经证明过。

智能优化算法在粒子滤波中的应用，成为粒子滤波史上的一大突破。基于人工鱼群算法［5］的粒子滤波(AFSA－PF)是一种模拟鱼群在自然环境中的生态行为的随机搜索最优值的滤波方法，使先验粒子向高似然域移动，从而改善粒子分布，提高粒子滤波估计精度.但是AFSA－PF 也存在着后期收敛较慢的问题，只适合在目标跟踪精度要求不是很高的场合。基于粒子群优化的粒子滤波算法(PSOPF)［6］保留了PSO 算法计算效率高，收敛快速的特点［7］，解决了粒子重要性采样过程次优的问题，改善了样本的分布，加速了粒子集的收敛，使得粒子滤波的性能得到很大的提高，并得到了广泛应用［8］。但是由于粒子都向最优方向移动，使得粒子趋向同一化，容易出现进化停滞的问题，并且计算结果不稳定。

本文在分析了以上两种算法的优缺点的基础上，取长补短，提出一种适用于闪烁噪声下机动目标跟踪的混合优化粒子滤波算法。该算法先利用人工鱼群的全局敛性寻找到满意的粒子信息值域，再利用粒子群算法进行快速的局部搜索，更新修正粒子的信息，使得本文算法不仅具有快速的局部搜索速度且具有全局收敛性能。仿真结果表明，该混合优化粒子滤波算法在闪烁噪声下精度高，鲁棒性强，抗干扰能力强，适用于雷达目标跟踪。

1 粒子滤波

离散的动态系统状态空间模型可描述为其中，xt∈Rn为时刻t 的状态变量，zt∈Rm表示传感器在时刻t 得到的测量向量，wt∈Rn和vt∈Rm表示相互独立的过程噪声和观测噪声，ft:Rn×Rm→Rn是状态转移函数，ht:Rn×Rm→Rm为传感器的量测函数。

粒子滤波是一种基于蒙特卡罗方法和递推贝叶斯估计的统计方法［10－12］，粒子滤波通过寻找状态空间Rn中的加权随机样本来近似后验概率密度p(xt|z1∶t).为了避免粒子的匮乏现象，Gordon等［13］提出了重采样的方法，其主要思想是去除权重小的粒子，复制权重大的粒子。

2 AFSA 算法

人工鱼群算法是一种模拟鱼群行为的随机搜索优化算法，它从构造动物简单的底层行为做起，通过人工鱼个体的局部寻优行为，最终在群体中使全局最优值突现出来。其数学模型描述如下:假设人工鱼个体的状态可表示为向量X =(x1，x2，…，xn)，其中xi(i=1，…，n)为欲寻优的变量;人工鱼当前所在的位置的浓度为Y=f(X)，其中Y 为适应度函数值;人工鱼个体之间的距离表示为di，j= ‖Xi－ Xj‖，visual 表示人工鱼的感知范围;δ 表示拥挤度因子;step 表示移动步长。人工鱼的行为描述如下:

1)觅食行为

当鱼发现食物时，会向食物逐渐增多的方向快速游去。即:

式中，s 表示人工鱼移动的最大步长;r 为介于(0，1)之间的一个随机数。人工鱼当前的状态为Xi，适应度函数值为Y.

2)聚群行为

鱼在游动过程中为了保证自身的生存和躲避危害会自然地聚集成群。即:

Else 执行觅食行为。

式中，视野内的伙伴数目为nf和中心位置Xc.

3 PSO 算法

粒子群算法是一种有效的全局寻优算法，它是基于群体智能理论的优化算法，通过群体中粒子的合作与竞争产生的群体智能指导优化搜索。PSO 算法可以表述为:随机初始化一个数量为m，维数为n的粒子群，其中，第i 个粒子的位置为Xi=(xi1，xi2，…xin)，速度Vi=(vi1，vi2，…vin).每一次迭代，粒子通过个体极值Pi= (Pi1，Pi2，…，Pin)和全局极值G=(g1，g2，…gn)来不断更新自己的速度和位置，从而达到寻优。更新公式如下

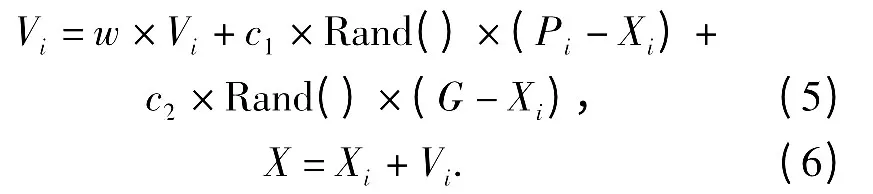
式中，Rand 是介于在(0，1)区间内的随机数;w 为惯性系数，w 若较大，则全局搜索能力强，w 若较小，则局部搜索能力强;c1和c2为学习因子。

4 人工鱼群与微粒群混合PF 算法

本文算法将基于AFSA 和PSO 的混合智能优化算法融入粒子滤波，并且将该混合粒子滤波算法应用到雷达机动目标跟踪模型中，为了更好地满足雷达跟踪的精度要求和实时性要求，在算法中加入时视步系数α，有效降低了出现局部极值的概率;并且提高了中间的阈值，增加了运算速度。本文算法思想如下:在粒子信息的更新与修正的过程中，由于PSO 往往容易陷入局部最优，对精度产生影响，所以先利用AFSA 的全局收敛性进行全局搜索，在全局的范围内找到粒子信息的满意的解域，增加全局有效样本的数量，减轻粒子滤波的退化现象，这样便可以克服PSO 算法容易陷入局部最优的缺点，然后再利用PSO 方法，通过粒子之间的合作与竞争来优化粒子信息，增加样本的有效性，提高粒子滤波的精度和收敛速度。基本流程如下:

1)初始化:在k=0 时刻，从重要性函数采样N个粒子，采样得到的粒子用表示。重要性密度函数取转移先验:

2)重要性权值计算

令适应度函数

3)设中间变量Pik和Gk，分别用于记录k 时刻粒子i 所经历的最好的状态值与粒子群所经历的最好的状态值;

4)执行人工鱼群的觅食行为和聚群行为。设粒子i 的当前状态为Xik，在感知范围内随机选择一个粒子，该粒子的状态为Xjk.

a.觅食行为:若Yik＜Yjk，粒子通过比较适应度函数不断更新自己的状态，使自己向更真实的状态靠近，否则，粒子Xik随机移动一步，成为新状态。为了防止粒子过早的聚集在极值点附近或出现局部极值，从而对本算法中的PSO 阶段造成影响，本文算法在这里加入视步系数α，一般情况下，取α 等于1或略小于1，可以保证算法快速收敛和较高的精度。在局部极值突出或函数变化非常平缓的情况下，应适当减小α 的取值。经仿真对比，在本文的模型中，当α≈0.9 时，效果最满意。

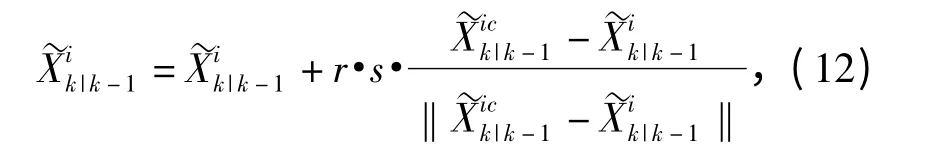
否则执行觅食行为。

5)判断鱼群算法是否终止。通过以适应度函数前后偏差小于阈值为条件，若终止，则鱼群算法终止，否则执行4).从雷达跟踪目标实时性的角度考虑，本文混合算法在此处的阈值应该略高于AFSAPF 的阈值，由此提高计算效率。通过仿真对比，在此处取较高一些的阈值对本文算法精度影响不大，这是因为接下来的PSO 阶段可以对粒子的信息进行更新和修正，引导粒子向高斯然区域移动。

6)通过比较适应度函数，将粒子i 的所经历的最优状态值赋给Pik.将N 个粒子中的适应度函数值最大的粒子的状态赋给Gk.

7)根据式(5)和式(6)更新粒子的状态.

8)权重归一化:

10)判断算法是否终止(通常为判断是否达到足够好的目标值)。若终止，则算法结束，否则转到6).

11)状态输出。

状态估计:

方差估计:

5 模型建立

5.1 机动目标模型的建立

假设雷达目标的运动都是带有连续转弯的非线性的运动，状态方程和测量方程分别为

其中:其中A 为系统矩阵，B 为系统噪声矩阵，W为扰动和模型误差引起的系统噪声，X(t)=［x(t)，vx(t)，y(t)，vy(t)，w］为目标状态向量，其中，x 和y为目标位移，vx和vy为对应的x，y 方向的速度分量。w 为运动角速度，即代表模型机动情况的参数，单位为rad/s.若w ＞0 表示左转弯，w ＜0 表示右转弯，w=0 则表示匀速直线运动，T 为采样时间。

5.2 观测噪声模型的建立

在雷达机动目标跟踪中，由于复杂目标不同部位的散射强度和相对相位的随机变化，会造成闪烁噪声。闪烁噪声具有明显的非高斯特性，它具有显著的“厚尾”特性［14］，严重影响了传统基于高斯假设的滤波器的性能。Hewer 等认为雷达闪烁噪声可以分解为高斯噪声和具有“厚尾”特性的噪声之加权和［15］。

本文采用高斯分布与拉普拉斯分布合成闪烁噪声的方法，为了方便地观察闪烁噪声的变化对本文算法精度的影响，引入参数ε 和λ，该闪烁噪声的概率密度可以表示为

式中，ε∈［0，1］表示闪烁噪声发生概率;λ 用于控制闪烁噪声的幅度，pg(x)表示高斯密度函数;pt(x)表示“厚尾”函数(拉普拉斯密度函数)。在一维零均值的情况下可以表示为

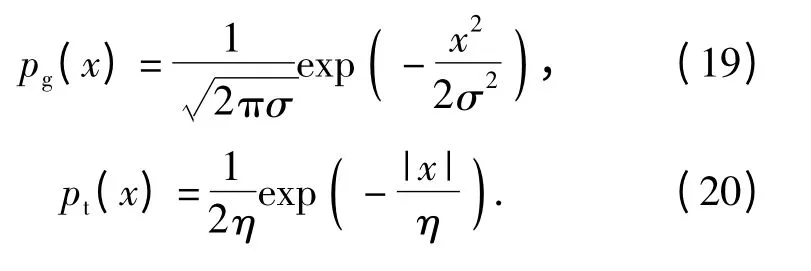
当高斯噪声均值为0，高斯噪声方差σ=0.001，拉普拉斯分布参数η =0.05，分配系数ε =0.05，λ=5 时，合成了一个在实际雷达观测中典型的闪烁噪声，合成的闪烁噪声记录见图1.

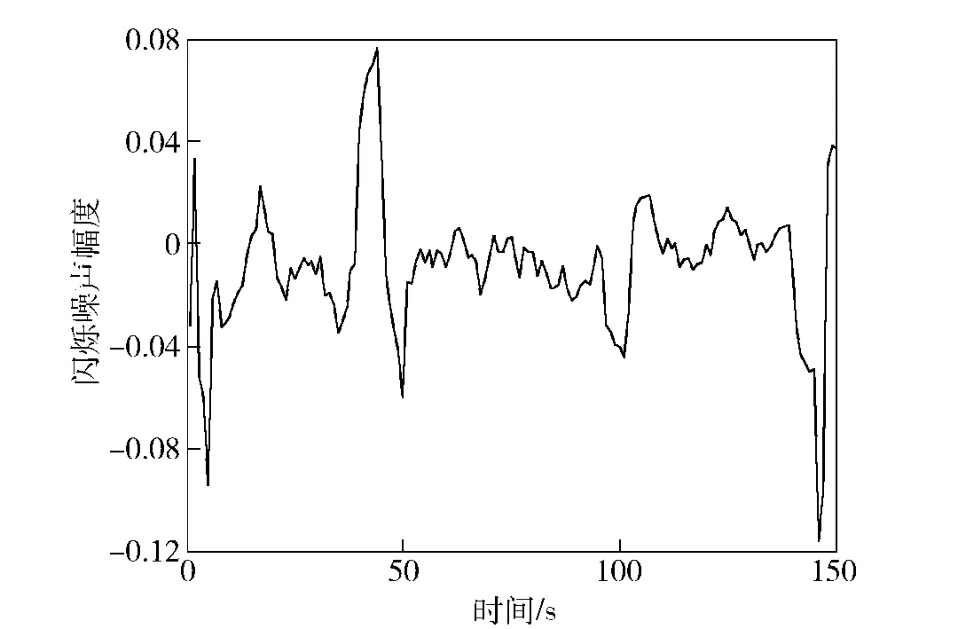
图1 闪烁噪声记录Fig.1 Licker noise record

6 仿真结果与分析

采取上文描述的非线性的转弯模型作为机动目标的运动模型，跟踪二维平面内的连续转弯的单机动目标，假设目标初始位置位于(1.25 ×105，1.0 ×105)m，初始速度(－100，－100)m/s，机动目标在前25 s 作匀速直线运动，从第26 s 到45 s 作角速度w=4.77°/s 的匀角速度转弯运动，第46 s 到65 s 继续作匀速直线运动，第66 s 到85 s 作角速度w =6.56°/s 的匀角速度转弯，从第86 s 到第100 s 再作匀速直线运动，101 s 到125 s 作角速度w =－5.96°/s 的匀角速度转弯，从第126 s 到第150 s 再作匀速直线运动。取采样周期为1 s.热噪声观测距离标准差为10 m，方位角标准差为0.1°;闪烁效应对应的观测距离标准差为100 m，方位角标准差为0.2°.分别用PF、AFSA－PF、PSO－PF 和本文的混合粒子滤波算法进行300 次蒙特卡洛仿真，仿真粒子数为100，调整ε 和λ，得到以下仿真结果:

1)当ε=0.05，λ=5 时，取单次仿真结果，从图2可以看出，当闪烁噪声发生概率较小，幅度较小时，AFSA－PF、PSO－PF 和本文算法均能够较好地跟踪目标。从图3，图4可以看出，此时各种滤波算法中，PF 的跟踪误差最大，特别在125 s 到达最后一个拐弯处后，容易出现发散现象;而本文算法的误差最小，发散现象不明显。

图2 小闪烁噪声下的轨迹跟踪Fig.2 Target tracking trajectory under weak glint noise environment

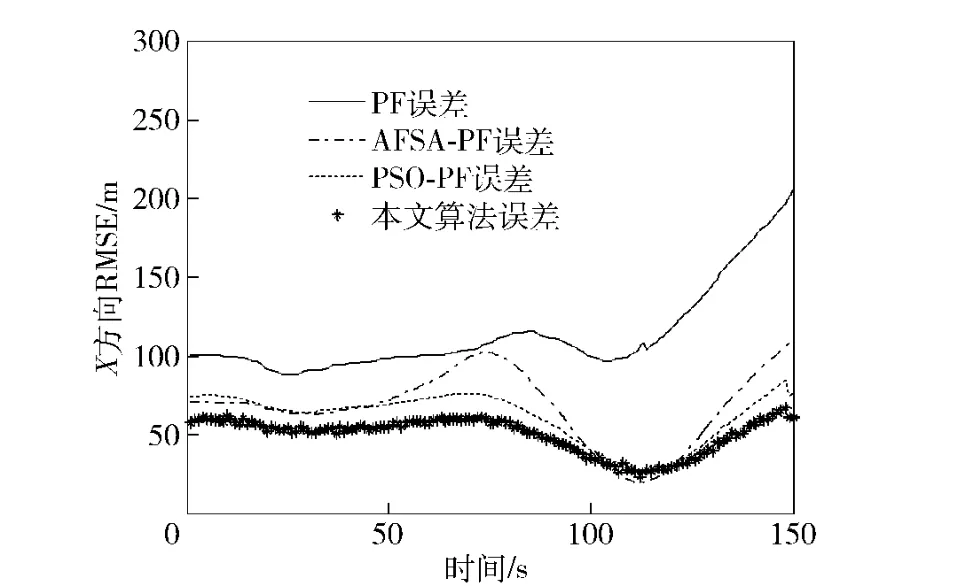
图3 小闪烁噪声下的X 方向的RMSEFig.3 Target tracking X－RMSE under weak glint noise environment

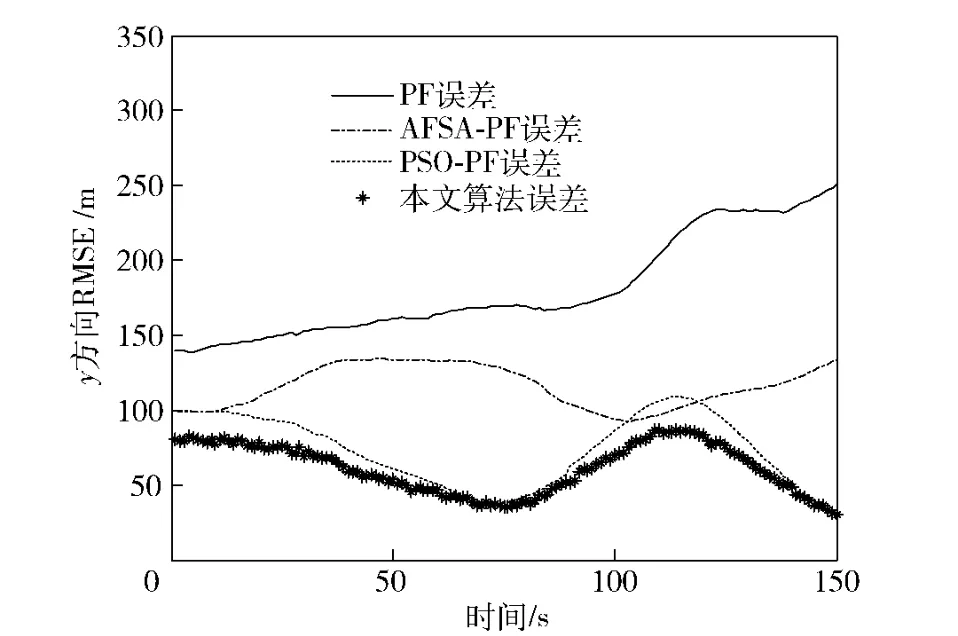
图4 小闪烁噪声下的Y 方向上的RMSEFig.4 Target tracking Y－RMSE under weak glint noise environment

2)当ε=0.1，λ=10 时，取单次仿真结果，从图5～7 可以看出，当闪烁噪声发生概率较大，幅度较大时，PF 算法，AFSA－PF 算法、PSO－PF 算法跟踪误差较大出现了明显的发散现象，跟踪轨迹与真实轨迹吻合程度较差。而本文算法跟踪效果则比较满意，跟踪误差最小。

图5 强闪烁噪声下的轨迹跟踪对比Fig.5 Target tracking trajectory under strong glint noise environment

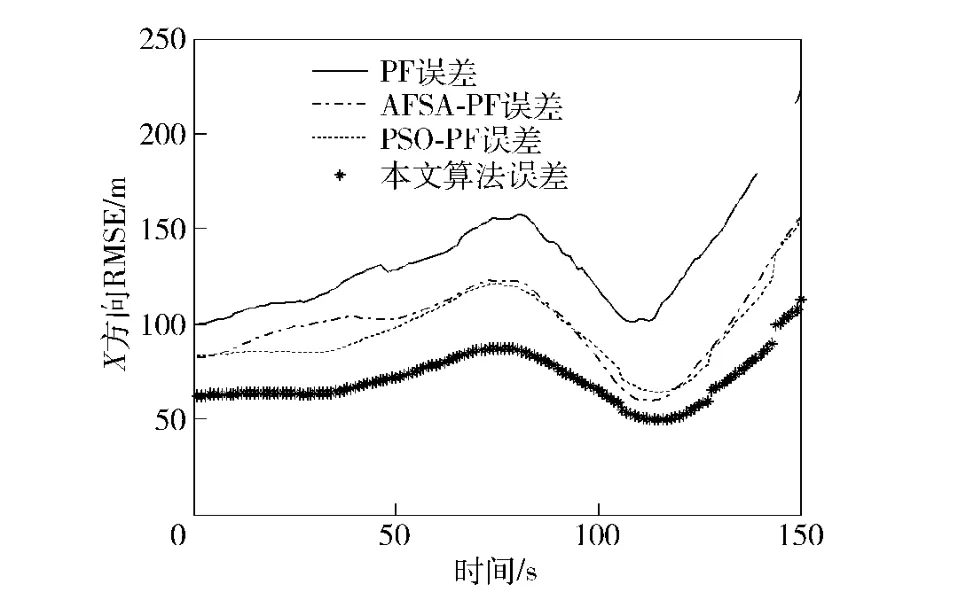
图6 强闪烁噪声下的X 方向的RMSEFig.6 Target tracking X－RMSE under strong glint noise environment

图7 强闪烁噪声下的Y 方向的RMSEFig.7 Target tracking Y－RMSE under strong glint noise environment

表1 连续转弯模型仿真结果比较Tab.1 Comparison of simulation parameters by continuous turn model

3)从表1可以看出，在粒子数相同的条件下，当闪烁噪声较小时，本文算法的误差最小，但和AFSA－PF，PSO－PF 相比，精度有较小幅度的提升。在运行时间方面，PSO－PF 的运行时间最长，其他3 种算法运行时间相当;而当闪烁噪声较大时候，本文算法在精度方面出现了明显的优势，误差变化幅度最小，说明了其鲁棒性强，其余3 种算法在闪烁噪声增大时候，误差出现大幅度的增加，鲁棒性差。这是由于本文算法在AFSA 阶段进行全局寻优时，虽然在强闪烁噪声的干扰下导致寻找满意解域的误差增大，但是在随后的PSO 阶段中粒子可以通过自身信息和群体信息不断修正自己的值，从而大大提高了精度。当粒子数增加到500 时，PF 的精度明显提高，说明了PF 对粒子数的依赖性很强;而其余3 种算法的精度并没有明显提高，说明了基于智能优化算法的粒子滤波对粒子数量的依赖性不强，这从另一方面也说明了本文算法在粒子数较小的情况下就能达到满意的结果。

7 结论

本文将人工鱼群与微粒群混合优化粒子滤波算法应用到闪烁噪声机动目标跟踪模型中，，利用人工鱼群算法的良好的全局收敛性和粒子群算法快速的收敛速度，取长补短，较原先两种算法，有着更高的搜索效率和收敛精度。仿真结果表明，本文算在强闪烁噪声下，保证目标跟踪的精度，取得满意的跟踪效果。在本文工作的基础上，可以考虑引入自适应视野和步长来减小计算量和提高寻优效率。

References)

［1］ Hewer M L，Martin R D，Zeh J.Robust preprocessing for Kalman filtering of glint nosie［J］.IEEE Transactions on AES，1987，23:120－128.

［2］ Sanjeev M，Maskell S.A tutorial on particle filters for online nonlinear/non－Gaussian Bayesian tracking［J］.IEEE Transactions on Signal Processing，2002，50:174－188.

［3］ Doucet A，Godsill S.On sequential Monte Carlo sampling methods for Bayesian filtering［J］.Statistics and Computing，2000，10(1):197－208.

［4］ Kong A，Liu J.Sequential imputations and Bayesian missing data problems［J］.Journal American Statistical Association，1994，89(2):278－288.

［5］ 李晓磊，邵之江，钱积新.一种基于动物自治体的寻优模式:鱼群算法［J］.系统工程理论与实践，2002，22(11):32－238.LI Xiao－lei，SHAO Zi－jiang，QIAN Ji－lxin.An optimizing method based on autonomous animats:fish－swarm algorithm［J］.Systems Engineering－Theory ＆ Practice，2002，22(11):32－ 238.(in Chinese)

［6］ 方正，佟国峰，徐心和.粒子群优化粒子滤波方法［J］.控制与决策，2007，22(3):273－277.FANG Zheng，TONG Guo－feng，XU Xin－he.Particle swarm optimized particle filter［J］.Control and Decision，2007，22(3):273－277.(in Chinese)

［7］ Kennedy J，Eberhart R C.Particle swarm optimization［C］∥Proceedings of IEEE International Conference on Neural Networks.Perth:IEEE，1995:19422－1948.

［8］ 姚祥光，周永权，李咏梅.人工鱼群与微粒群混合优化算法［J］.计算机应用研究，2010，27(6):2084－2086.YAO Xiang－guang，ZHOU Yiong－quan，LI Yiong－mei.Hybrid algorithm with artificial fish swarm algorithm and PSO［J］.Application Research of Computers，2010，27(6):2084－2086.(in Chinese)

［9］ Krohiling R A.Gaussian swarm:a noverl particle swarm optimization algorithm［C］∥Proceedings of the IEEE Conference on Cybernetics and Intelligent Systems.Dalian:IEEE，2004:372－276.

［10］ Doucet A，Godsill S，Andrieu C.On sequential Monte Carlo sampling methods for Bayesian filtering［J］.Statist Computer，2000，10:197－208.

［11］ Doucet A，de Freitas J，Gordon N.An introduction to sequential Monte Carlo methods［M］.New York:Springer，2001:3－14.

［12］ Sanjeev M，Simon M.A tutorial on particle filter for online nonlinear/non－Gaussian Bayesian tracking［J］.IEEE Transactions on Signal Processing，2002，50(2):174－188.

［13］ Gordon N，Salmond D.Novel approach to non－linear and non－Gaussian Bayesian state estimation［J］.Proceedings of Institute Electric Engineering，1993，140(2):107－113

［14］ Durovic Z M，Kovacevic B D.QQ－plot approach to robust Kalman filtering［J］.International Journal of Control，1994，61(4):837－857.

［15］ Gordon N，Whithy A.A Bayesian approach to target tracking in the presence of glint［J］.Signal and Data Processing of Small Targets，1995:472－483.