响应曲面法在现金流预测中的应用

刘洪久，胡彦蓉，Robert Rieg，马卫民

(1.常熟理工学院，江苏 常熟 215500；2.Hochshule Aalen，Aalen，德国 73430；3.同济大学，上海 200092）

0 引言

现金流是企业生命的血液，是衡量企业经营绩效的重要指标，是企业价值的具体体现。没有现金流，企业生存和发展就失去了基础。是现金流将公司的日常经营以及投融资活动紧密地联结在一起,其大小不仅决定着公司的支付能力，更是企业增长和创造价值的财务源泉。因此，不管是决策者、投资者和银行，如果能对企业未来的现金流量作出较为准确的预测，就可以对企业未来经营业绩作出完整客观的综合评价[1]，从而进行科学合理的决策。本文采用的响应曲面法是一种回归设计的方法。该方法通过寻找未来现金流量和历史现金流量间的定量规律（而不是判断因子的显著性，找出各因子水平的最佳组合）预测未来现金流量。

1 样本数据来源和滑动窗参数的确定

1.1 样本数据来源

如果样本数据不同，很难判断方法的优劣。为了测试研究方法预测的准确性，需要采用同一数据。这里采用一汽轿车（股票代码000800）从2002年12月31日到2011年3月l5日34个现金流数据（每季度）。现金流量用CFt表示（t=0，1，…，n），n表示时间序列的长度。

为了便于仿真，所有的数据都被归一化（0，1），如公式（1）：

式中CFtmax和CFtmin分别表示现金流时间序列的最大值和最小值。

1.2 滑动窗参数确定

滑动窗口包括发送器和接收器，发送器和接收器的尺寸大小分别用wt和wr表示[2]。为了研究在什么样的尺寸下，模型具有良好的预测效果，需要确定合适的发送器的尺寸[3]，为此我们改变wt从1到8（wt=1，2，… ，8）)。接收器的大小为1（wr=1）（见图1），因为模型的输出仅有一个结果。这样，当我们同时滑动发送器和接收器的时候，就会得到模型的输入矩阵P(i,j)(i=1，2，…，wt；j=1，2，…，n-wt)和输出矩阵T(j)(j=1，2，…，n-wt)（见公式2、3）。

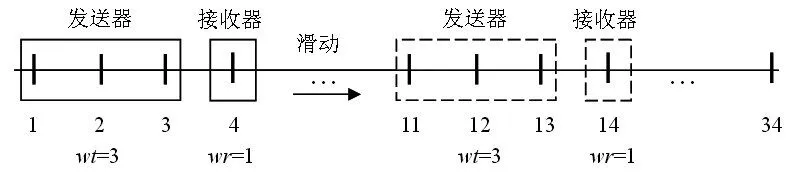
图1 滑动窗口的发送器和接收器（wt=3）

P(i，j)和T(j)各自被划分为培训数据和测试数据两组，每组培训和测试数据都包括P(i，j)和T(j)。例如，数据组1由P(1，j)和T(1)(j=1，…，wt)。测试数据组中包含三对输入和输出向量用于检验模型的性能，培训数据组用来训练模型。

如果我们假定t时间的现金流量由t-1，t-2，…，t-wt时刻的现金流量决定，那么我们会构建函数f：Rwt→R的映射，从而得到t时刻的CF估计值：

2 响应曲面模型的建模和仿真

在统计学中，响应曲面法（RSM）主要用于构建多个解释变量和一个或多个响应变量之间的关系，该方法是1951年由Box和Wilson提出[4]。RSM是一种优化生物过程的统计学试验设计，采用该法以建立连续变量曲面模型，对影响生物过程的因子及其交互作用进行评价，确定最佳水平范围[5]。如果设y代表输出，xi(i=1，2，…，n)代表输入，响应曲面方程可以表示为公式（6）。

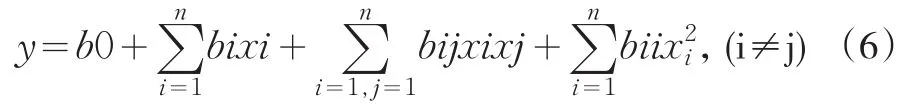
式中：

b0—常数项；

bi—一次项系数；

bij—交叉项系数；

bii—二次项系数。

模型在Matlab 2009b环境中训练和测试，需要引用Matlab统计工具箱中的rstool函数计算b0，bi，bij，bii。对于函数rstool，有四个函数可以选择：Linear，Pure Quadratic，Interactions和Full Quadratic。

Linear—方程包括常数和一次项系数；

PureQuadratic—方程包括常数项、一次项和二次项系数；

Interactions—方程包括常数项、一次项和交叉项系数；

Full Quadratic—方程包括常数项、一次项、交叉项和二次项系数[6]。

四个函数的训练效果取决于它们的均方根误差的大小。显然，均方根误差越小，模型的训练效果越好。我们将训练样本数据输入各模型可得每个模型的均方根误差（见表1）。

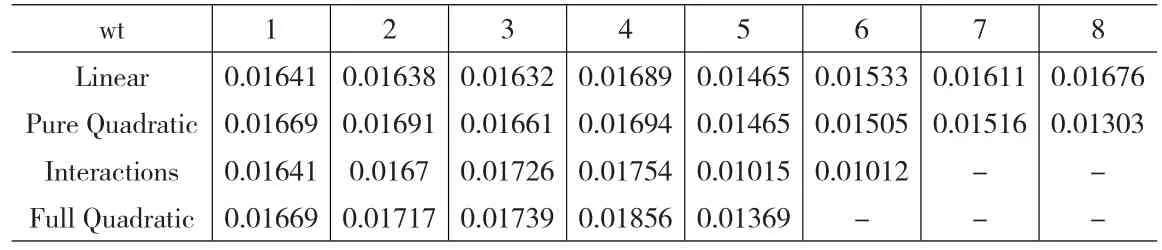
表1 不同函数的均方根误差rmse

根据表1数据，当wt等于6时，Interactions函数的拟合效果最好，均方根误差最小（rmse=0.01012）。图2是Interactions函数的训练结果图。

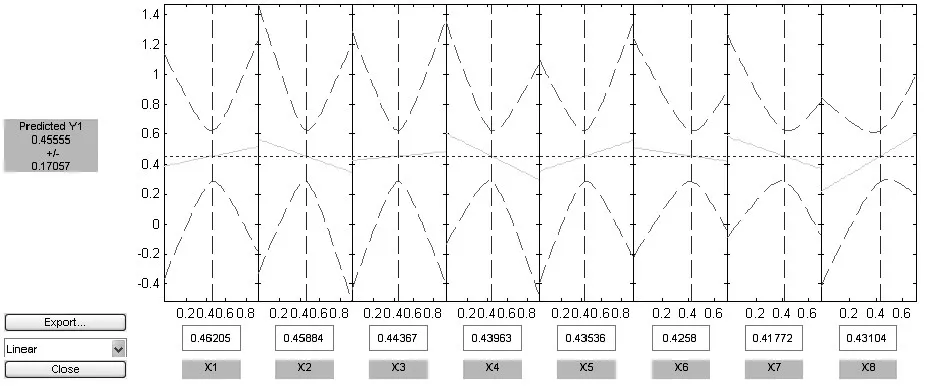
图2 Interaction函数的训练结果

将rstool函数的计算结果输入到Matlab的workshop可得在不同的滑动窗发送器尺寸下（wt=1,2,…,8），Linear、Pure Quadratic、Interactions和Full Quadratic函数的各项系数b0、bi、bij和bii。将各项系数和测试数据带入公式（6），可计算预测值的相对误差。具体见表2。

观察表2，我们会发现，滑动窗发送器的尺寸为wt=7，训练函数为Linear时，预测的相对误差最小（8.0113%）（见图3）。对比模型的训练和测试过程，即表1训练的结论和表2测试的结论不一致，因为表1的结论为：wt等于6时，Interactions函数的拟合效果好。所以，在运用响应曲面模型时，不能单纯的运用样本训练的结论简单的去预测未来的现金流。要在对模型训练的基础上测试不同发送器尺寸和函数的条件下，才能得出合理的结论。

表2 预测值的相对误差

3 结论

通过对响应曲面法的建模和仿真，可以发现，作为一种回归设计方法，响应曲面模型与其它时间序列方法（指数平滑法、移动平均法、曲线趋势预测法等）一样，都具有良好的预测功能。响应曲面模型的训练效果和预测性能与滑动窗口的发送器尺寸wt和具体的响应曲面模型函数有关。通过对一汽轿车公司现金流预测的实证研究表明，当滑动窗发送器尺寸wt等于6时，Interactions函数的拟合效果好；而当滑动窗发送器的尺寸wt等于7时，Linear函数的预测相对误差最小。因此，应用响应曲面模型做预测时，既要考虑样本训练的结论，又要验证样本预测的效果，这样才能合理的预测企业的现金流，从而为科学决策提供依据。

图3 RSM法中wt=7时的预测效果

[1]韩立岩,娄静.经营、投资和筹资现金流动态交互影响分析[J].中国管理科学,2010,(2).

[2]Khan M S,Coenen F,Reid D,et al.A Sliding Windows Based Dual Support Framework for Discovering Emerging Trends from Temporal Data[J].Knowledge-Based Systems,2010,23(4).

[3]Chu C J.Time Series Segmentation：A Sliding Window Approach[J].Information Sciences,1995,85(1～3).

[4]Box G E P,Wilson K B.On the Experimental Attainment of Optimum Conditions[J].Journal of Royal Statistical Society,1951,8(1).

[5]Crispim E G,Piai J F,Muniz A F R A.Addition of Methacryloil Groups to Poly(Vinyl Alcohol)in DMSO catalyzed by TEMED：Opti⁃mization through Response Surface Methodology[Z].2006.

[6]周纪芗,茆诗松.求响应曲面的极小极大估计的计算机方法[J].华东师范大学学报(自然科学版),1983,(3).