独立分量分析在信号处理中的应用

李 伟,王 璠，李 颖，王少凡

（东北石油大学 机械科学与工程学院，黑龙江 大庆 163318）

早期还没有出现ICA这个名词，80年代早期，该方法由J.Herault.C.Jutten与B.Ans提出来。在Jutten回顾中，该问题首次出现在1982年的神经生理学框架当中。即在肌肉痉挛中，最简单运动译码模型里，输出x1（t）和x2（t）表示测量肌肉痉挛传感器信号，而sl（t）和s2（t）是运动关节的尖角状态与速率。当时，设想的ICA模型所支撑的信号之间并不是合理的。由测量响应x1（t）和x2（t），神经系统以某种方式可以推出状态和速率s1（t）与s2（t）。要获悉可逆模型，一种可能是在简单的神经网络中使用非线性去相关原理。Herault和Jutten提出了特殊的反馈网络解决该问题。

整个80年代，ICA研究主要集中在法国研究者当中，其国际性影响力仍然很有限。在80年代中期，国际性的神经网络会议上，少有ICA呈文，很大程度上被埋没在令人感兴趣的反向传播的洪流之中。那个时代，Hopfield网络，以及Kohonen的自我组织映射(SOM)正活跃地传播着。另一个相关的领域是高阶谱分析，其首次国际性专题研究小组于1989年被组建。该小组中，早期的ICA论文是由J.F Cardoso与P.Comon发表的。Cardosos使用了代数学的方法，尤其是高阶累计量张量(tensor)，最终导出了JADE算法。四阶累计量的效用较早是由J.L.Lacoume提出米的。在信号处理文献当中，早期的经典论文是法国的一个小组发表。

1987年，利用3阶累积量，在某种不同的框架里，Giannak提出了ICA识别问题。然而，这种结果的算法要求穷举搜索。Lacoume和Ruiz也利用高阶统计量简述了一种数学方法来解决这个问题。Gaeta和Lacoume提出了由最大相似法估计混合矩阵，在这里，也要求一种无遗漏的搜索，决定多数变量的对照函数的独立最大值。由此，从训练的观点来看，这仅仅在二维方面是实用的。

在信号处理中，盲信反卷积的相关问题已有一些早期的处理方法。特别地，该结论使用了多道(multi-channel)盲反卷积非常相似于ICA法。

80年代，科学工作者的著作得到了发展，这些人当中，A.Cichocki和R.Unbehauen首次提出了当前最流行的ICA算法之一。在90年代早期一些有关ICA和信号分离论文相继发表。“非线性PCA”法由此也提出来。然而，直到90年代中期，ICA的影响力仍旧相当小。提出的几种算法在运用时，通常要求某种约束问题，但是统计最优准则的提出，严格的约束似乎己经过时了。

Cardoso致力于代数学四阶累积量特征，并像线性算子作用于矩阵一样解释了它们。一种简单的解法是运行一个对角化给出ICA估计的累积矩阵的识别率。当运行被定义在一系列矩阵上时，运行获得提供更多的鲁棒性估计的几个联合的对角化累积矩阵。其它的代数解法，仅利用四阶累积量也有所研究。

Inouye提出了对于两种信源分离的解法，然而同时Comon提出了对于N大于或等于2的解法。与Cardoso的解法一起，这些是初次直接(在时域多项式)ICA问题的解法。Inouye和他的同事得出了对于ICA问题的识别条件。

ICA获得较广泛的注意和兴趣的是在A.J.Bell和T.J.Sejnowski发表的基于信息最大准则法之后。90年代中期，S.L.Amari与他的同事使用普通的梯度法改善了该算法，它的基本的关联是最大似然估计与证实的Cichocki-Unbehauen算法。两三年之后，当前的作者提出了定点(fixed-point)或称快速ICA(FICA)算法，由于它的计算上的有效性，对于较大尺度问题的ICA应用上有了很好的作为。

自从九十年代中期以来，致力于ICA的研究论文，专题研究小组和会议已急剧增加。第一个国际性ICA专题研究小组于1999年一月份成立于法国的Aussois，第二个专题研究小组于2000年七月份在芬兰首都赫尔辛基成立。两个小组聚集了超过100多位研究者从事ICA与盲源分离研究，从而促成了ICA的变革以及确定了成熟的ICA研究领域[1]。

1 ICA的基本理论

ICA的模型可描述为:假设N个独立的源信号s（t）=[s1（t），s2（t），…,sN（t）]T经过线性系统A混合在一起，得到M个观测信号x（t）=[x1（t）,x2（t），…，xM（t）]T，源信号和观测信号之间满足关系式:

其中A是一个M*N维的矩阵，源信号s（t）和混合矩阵A都是未知的，只有混合后的x（t）可以观测到。可以证明在M叟N的条件下，当混合矩阵A列满秩，源信号s（t）的各分量相互独立，且最多只有一个分量是高斯分布时，可以求得一个分离矩阵W使得:

其中 y（t）是 s（t）的一个估计，其各分量尽可能互相独立，且逼近 s（t），只是 y（t）各分量的排列次序和幅度可能与s（t）不同，这又称为ICA解的不确定性问题。假设是ICA的一个解，那么PDW也是ICA的一个解，其中P为置换矩阵(每一行和每一列都只有一个元素1),D为对角矩阵(对角元素非0，其它元素为0)。通常只考虑M=N的情况，当源信号完全分离出来时，有WA=PD，为了简化分析，木文在以后的分析中不妨假设PD=I，此时有WA=I。

为了求解分离矩阵W，通常是先设置一个目标函数L(W)，选择不同的目标函数可以得到不同的ICA算法，其中最大熵(Maximum Entropy,ME)算法和最大似然(Maximum Likelihood.ML)算法的目标函数可统一为[2～3]

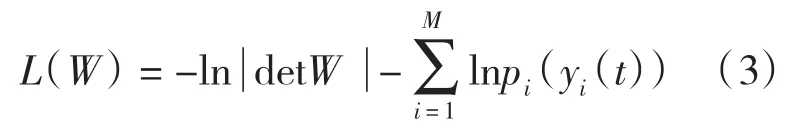
其中p（iy（it））是输出信号，y（it）的概率密度函数(pdf),是分离矩阵W的行列式的绝对值。

建立目标函数后再确定一种学习算法，通过迭代使式(2-3)中的L（W）达到最小值的即是ICA的解。学习算法大致分为两类，离线批处理方式和在线自适应方式[3]。前者是对一段时间内的信号进行迭代，后者对每一时刻的信号进行迭代。Beth和Sejnoeski提出了随机梯度学习算法[4]，其离线批处理迭代公式为

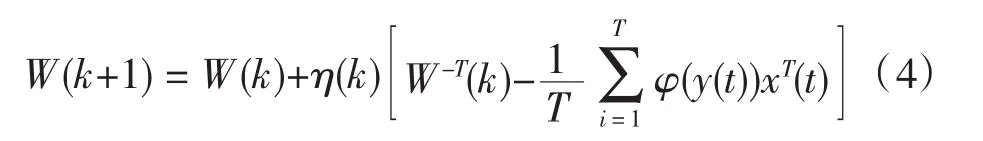
其中η(k)为学习率，T为每次处理的向量个数，φ(y(t))与源信号的分布及其假设有关，根据不同的情况有多种选取方法。该算法的缺点是收敛速度慢，需要对分离矩阵求逆。Amari在随机梯度的基础上提出了自然梯度学习算法，避免了矩阵求逆，加快了收敛速度，其离线批处理迭代公式为

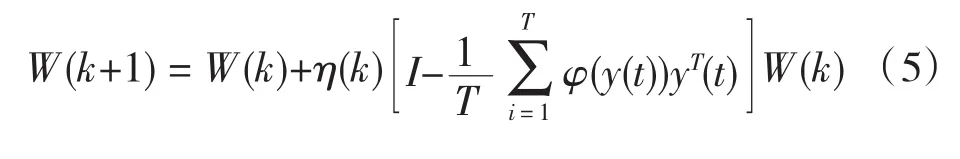
2 独立分量分析算法

2.1 数据预处理

某些ICA算法要求数据x的预白化，甚至这些算法不是必须要白化的，但通常白化的数据有更好的收敛性。前面说到的数据己假设为定中心化，即使其有零均值，白化就是将观察变量x线性变换为变量ν

上述ν的协方差矩阵等于单位矩阵:E{ννT}=I。该变换通常是可能的，真正地，它能够由传统的PCA方法来实现。除了白化外，PCA可能允许我们决定独立分量的数目(如果m>n):若噪声标准低，x能量基本上集中在由最先n个主分量组成的子空间上n是模型中的独立分童个数。估计信号(这儿指独立分量)数目己存在一些估计方法。因此局部维数降低的假设m=n将在这儿仍旧保持:

式中B=QA是一正交矩阵，因为

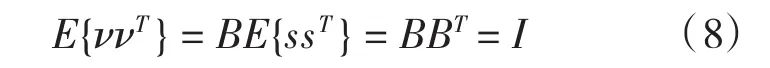
回忆我们假设独立分量si有单位方差，因此简化得到模型的任意矩阵A可转化为更简单的得到正交矩阵B的问题。一旦得到矩阵B，从观察到的ν，利用等式(3-3)解决独立分量如下：

这也是值得做的，虽然仅考虑球化解决不了分离问题，这是因为仅定义球化等于另外的旋转:若Qi是球化矩阵，然后当且仅当U为正交矩阵时，Q2=UQ1也是球化矩阵。因而，分离独立分量，必须得到正确的球化矩阵。首先得到任意球化矩阵Q，而后从合适的非二次标准决定合适的正交变换。

接下来，我们将假设在下面某些节中数据是白化数据。为简单起见，白化数据将表示为x，变换混合矩阵表示为A，前面章节有定义。如果算法必须预白化，这会在相应的章节中提出来，若没有提及到，说明该数据己白化过的。

2.2 Jutten-Herault算法

该算法的先期工作由神经网络激发灵感而来，他们算法是基于消去非线性相关。矩阵W的非对角项修正由下式给出:

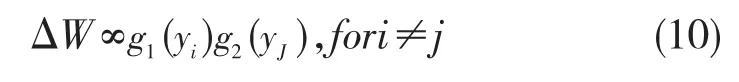
式g1与g2是某些奇的非线性函数，每次迭代像y=(I+W)-1x 计算 yi.。对角项 Wij置零。收敛之后，yi给出独立分量的估计。不幸的是，该算法的收敛仅仅在相当严格的约束下。

2.3 非线性去相关算法

比较Jutten-Herault算法，非线性去相关算法简化了计算量，避免了任何矩阵的逆与提高了稳定性。例如有下面的算法:

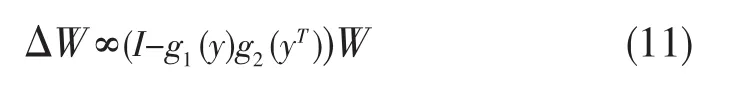
式中 y=Wx,非线性函数 g1(·)与 g2(·)被用来分离向量y每一个分量，恒等可以由任意正的有界限的对角矩阵代替、EASI算法如下:

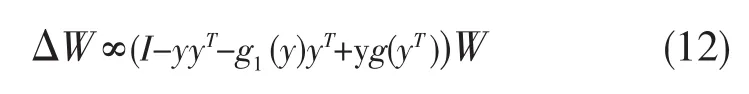
选取非线性函数的基本方法是利用后面小节中的描述的最大似然(或信息最大化)提出的学习规则。

2.4 非线性PCA算法

非线性PCA算法是神经PCA算法的非线性扩展，它的分级PCA学习规则的非线性形式如下所示

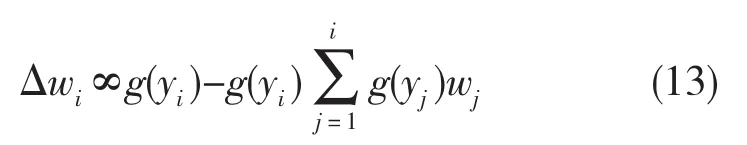
式中g是一个合适的非线性尺度函数。一般地，非线性的引入即是学习规则利用了高阶信息。因此学习规则可能完成了某些更相关的高阶表述技术(投影追踪、盲反卷积、ICA)。非线性PCA算法的一种有趣的简化形式是半梯度算法，学习规则(3-10)里的反馈项由更多简单的项代替，即

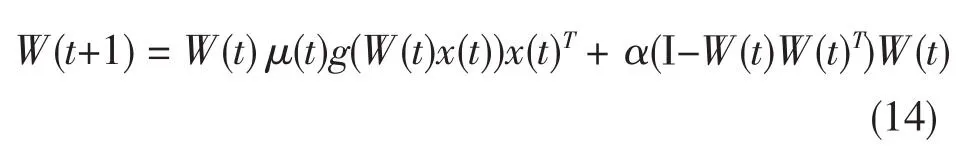
式中 μ(t)为学习率（步长）序列，α 为〔0.5，1〕范围内的常数，函数g被用来分离向量y=Wx的每一个分量，假设数据已白化。另外一种半梯度算法的分等级形式也是可能的。

2.5 神经单个单元学习准则

利用随机梯度下降原理，由前面的单一单元对照函数可以得出一种简单的算法。假设考虑白化数据。例如，获得关于w的一般式

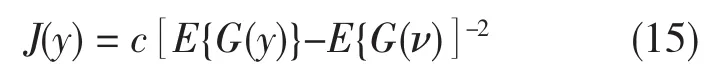
的对照函数的瞬间梯度，获得标准化w即||w||2=1，获得下面的Hebbian-like学习规则

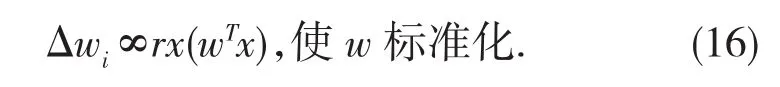
式中可能定义的常数，例如

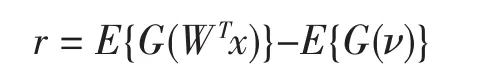
因此非线性函数g可以是大多数任意非线性函数。实际上正确估计:符号就足够。这样单一单元算法首次引入峰度，相应的 g（u）=u3。

2.6 其它神经（自适应)算法

其它神经算法包括:·探测投影追踪算法。由于ICA与投影追踪之间的紧密联系，投影追踪算法可以直接用来解决ICA问题并不觉得奇怪的;·基于非线性PCA标准的最小均方型算法;·与累计张量相关的自适应算法等。

2.7 快速ICA(FICA)算法

这节中，引进一种非常有效的方法，即适合该任务的最(极)大值化。同时这里假设数据实己经经过定中心和白化预处理。

（1）一个单元(one unit)快速ICA

起初，将说明单元快速ICA变换。这个“单元”是指计算上的单位，最后是一个人工神经元，有权向量w的神经元能够通过学习规则修正。快速ICA学习规则得到一种趋势，即单位化向量w以至预测wTx使非高斯最大化。在这里，非高斯式(3-10)给出的负嫡J(wTx)的近似值测得的。回想wTx的方差必需是单位化抑制对于白化数据等同于抑制w的范数的单位化。

快速ICA是基于为得到wTx非高斯最大值的定点迭代法。也可以是源于近似牛顿迭代法。用g表示非二次函数G公式推导用于是(3-11)；例如，式G1(u)=1/a1log cosh a1u与G2(u)=-exp(-u2/2)函数的公式推导是

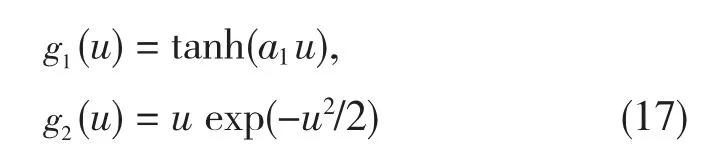
式中1≤a1≤2是某一合适的常数，通常取a1=1。快速ICA算法的基本结构如下:

（1）权向量w的初始化选择：

（2）假设w+=E{xg(wTx)}-E{g'(wTx)}w;

（3）假设w=w+/||w+||;

（4）若不收敛，返回2。

注意，收敛意思是新的和旧w值在同样的趋势上，即它们的点积(几乎)等于1。既然w和-w定义在相同的趋势上，向量收敛到单个点并不必要的。这又因为独立分量可以仅仅等于乘以符号来定义。这里假设的数据是经过预白化。

快速ICA公式推导如下：首先注意到，在E{G(wTx)}最优值上获得wTx负熵近似值的最大值。根据Kuhn-Tucker条件，在约束E{(wTx)2}=||W||2=1下,E{G(wTx)}的最优值由以下获得

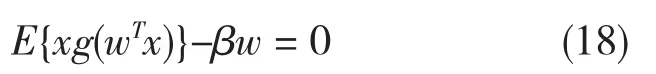
通过牛顿法来解决这个等式。(3-15)左边的函数用F表示，可得到它的Jacobian矩阵JF(w)为

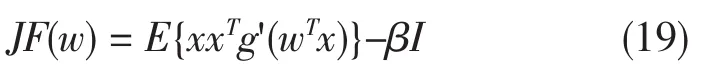
为了简化该矩阵的变换，我们决定近似式(3-14)的第一项。既然数据是限制在球形范围内，看起来合理的近似为：E{xxTg'(wTx)}≈E{xxT}E{g'(wTx)}=E{g'(wTx)}I。因此Jacobian矩阵变成对角矩阵，且能够容易转化。从而得到如下的近似牛顿迭代法:

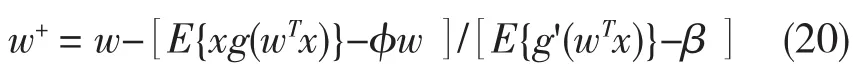
该算法可以通过在等式两边同乘以β-E{g'(wTx)}更加简单化。代数简化后，这里给出了快速ICA迭代法。

实际上，快速ICA中的期望必须由它们的估计所取代。正常的估计具有的期间内等于样本的均值。真正地，虽然所有的数据应该利用到，但是这常常不是一种好的方法，因为计算量可能要求太大。然后用较少的样本估计平均数，样本的数量在最后的估计上可能有不可忽视的影响。应该在每一次迭代分离的选择样本值。如果收敛不满足，而后可能要增加样本的数量。

（2）几个单元(several units)快速ICA

前述小节中的一个单元估计只是独立分量之一，或者一个预测追踪趋势。为估计几个独立分量，我们有必要运行一个单元的快速ICA算法使用有权值 w1，…，wn的几个单元(例如多个神经元)。

为了避免不同的向量收敛于同一个最大值，每一次迭代之后，必须使输出wTx,…,wTx去相关。这里我们提出二种方法来实现。

一种简单的方法是基于Gram-Schmid-like去相关的紧缩法。意思是一个一个地估计独立分量。当估计了p个独立分量，或P个向量w1,…，wP，对wp+1运行一个单元定点算法，且每次迭代步骤从wp+l减去“预测”，，即前 p 个估计向量，然后标准化wp+1，

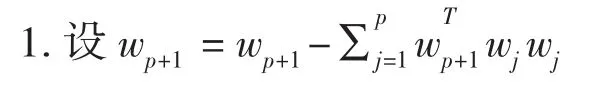
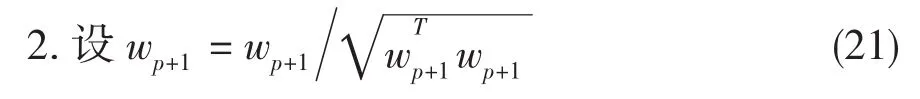
然而某些应用中，可能希望使用对称去相关。例如，这可以由把矩阵开平方根的方法实现，

式中 W 使向量矩阵(w1，…，wn)T，从 WWT=F△FT(当(WWT)-1/2W=F△-1/2FT)特征值分解包含了平方根的逆(WWT)-1/2。一种更简单的选取是下面的迭代算法，

1.设 W=W/sqrt(‖WWT‖)

2.设W=3/2W-1/2WWTW

第一步中的范数几乎可以是任何普通的矩阵范数，例如，二维范数或最大绝对值的行(或列)的和(但不是Frobenius范数)。

快速ICA有神经算法的大多数优点:并行，分布式，计算最简单，且要求较少的内存空间。随机梯度法看起来是更可取的，如果仅当环境改变时要求快速自适应。

2.8 算法选取

总之，ICA算法的选择是基于自适应与匹配模式算法之间的选择。

自适应情形通过随机梯度法获得算法，这种方法同时估计出所有的独立分量，大多数流行的算法是这类基于似然或相关对照函数的神经梯度上升，如信息最大化(infomax)。对于单一单元情形，简单的随机梯度法给出了自适应算法(最大化负熵或它的近似)。

匹配模式情形在计算上是更有效的算法，对于低维数据，基于张量法是有效的，但是使用于高维情形。基于定点迭代的快速ICA算法是一种非常有效的匹配算法，它既可用于最大化单个单元对照函数，也可用于多单元对照函数，还包括似然。

3 主要应用

（1）盲源分离(BBS)

最简单的盲源分离问题即假设M未知，独立信号为 s1（t），s2（t），…，sm（t）。信源混合一未知线性M*M矩阵A产生观察信号x1（t），x2（t），…，xn（t）。该过程可由下面等式表示:

式中,s（t）=[s1（t）,s2（t）,…,sm（t）]是M*1的源信号列向量；x（t）=[x1（t），x2（t），…,xn（t）]是观察混合信号向；A称为混合系统(或矩阵)。

观察信号 x（t）通过该系统后得到近似于 s（t）的输出y（t）。该过程可由下式表示:

衡量一组信号是否接近互相独立，现在出现了多种准则，即优化判据。因为问题没有唯一解，只能在某种优化判据下寻求它的近似解答，使y（t）中各分量尽可能互相独立。

考虑这样一种情形，有几个信号，由几个自然的对象或信源发出。例如，这些自然的信源可能是不同脑区域发出的电信号[5]；人们在同一房间中说话发出的语音信号[6]；或移动电话发出的无线波等。

（2）特征提取

另一个应用是特征提取。其主要应用于水印图像的提取[7]。另外应用于数据压缩和模式识别[8]等特征也是重要的研究课题。

（3）盲反卷积

ICA方法很少直接应用于盲反卷积。盲反卷积广泛用于通信、雷达、地震[9]和图像等各个方面。例如，在数字无线通信系统中，由于多径或信道衰落引起的码间干扰(ISI)可用自适应均衡技术消除。对时变信道，往往需要定时发送训练序列，以便跟踪信道参数的变化，这大大降低了信道的利用率，而盲均衡可以较好地解决这一问题[10]。

（4）其它方面

一方面由于ICA和投影追踪，一方面由于ICA与因子分析之间的紧密联系，投影追踪与因子分析的应用也可以利用ICA来实现成为可能。这包括诸如经济领域[11]、心理学以及其它社会科学领域，以及密度估计和回归(初步)数据分析。

4 发展趋势

现在独立分量分析方法已经广泛的应用于医学，图像处理和机械故障诊断等方面。并且已有很多的研究人员将独立分量分析方法于小波分析方法、神经网络及主分量分析等其他信号分析方法结合使用，在实际应用中取得了良好的效果，而这种多种分析方法相结合的分析方法也必将成为未来独立分量分析方法的发展方向。

尽管目前独立分量分析方法仍存在一定的局限性，但随着研究的进一步深入，相信独立分量分析方法必将在更多的领域有所应用。

[1]张新军.独立分量分析及其在多通道信号处理中的应用研究[D].汕头大学硕士学位论文，2003:15-16.

[2]Amari S,Chen T P,Cichocki A.Stability analysis of learning algorithms for blind source separation[J].Neural Networks,1997,10(8):1345-1351.

[3]杨行峻，郑君里.人工神经网络与盲信号处理[A].2003:21.

[4]Bell A,Sejnowski T J.An information-maximization approach to blind separation and blind deconvolution[J].Neural Computation,2005,7(6):1129-1159.

[5]翟 葵，吴小培.基于独立分量分析的脑电信号消噪[J].现代制造工程 2006（2）：90

[6]赵彩华，刘 琚，孙建德，闫 华.基于小波变换和独立分量分析的含噪混叠语音盲分离[J].电子与信息学报2006（09）：78.

[7]Jian Ji,Zheng Tian.Robust ICA Neural Network and Application on Synthetic Aperture Radar(SAR)Image Analysis[A].Lecture Notes in Computer Science.2006:108-110

[8]王 岩.基于独立分量分析与神经网络的电子鼻模式识别[D].西南交通大学硕士学位论文.2006：41.

[9]李国福，曹思远，周 鹏，韩瑞东.地震去噪中的P-ICA方法[C].中国地球物理第二十一届年会论文集，2005：87-89.

[10]李鸿燕，王华奎，独立分量分析在混叠通信信号分离中的应用[J].仪器仪表学报，2006（s1）：66

[11]党 红.权益结合法的发展路径分析[J].财会通讯(学术版)，2006（4）：21.