数控机床运行状态数据采集及数据处理技术研究

韩兴国

（桂林航天工业高等专科学校机械工程系，广西 桂林 541004）

通过几个五年计划的努力，我国的数控机床已有了很大的发展，数控技术正在向高速化、高精度、网络化的方向发展。对数控机床生产厂家和用户来说，拥有能够直接或间接证明其数控机床运行是否平稳，对数控机床的运行状态做出一个客观、正确、公正、综合的评价的检测方法至关重要。特别是对数控机床生产厂家来说，若能在装配联机调试之前快速、准确的测知数控机床的运行状态和运行精度，把数控机床出现故障的可能性在联机调试之前发现并予以消除，将能极大提高数控机床的装配调试效率。

1 数控机床运行状态数据采集原理

1.1 光电编码器

多数数控机床都装有光电编码器，它是一种通过光电转换将输出轴上的机械几何位移量转换成脉冲或数字量的传感器，编码盘直接装在旋转轴上，以测出轴的旋转角度位置和速度变化，其输出信号为电脉冲。

光电编码器随被测轴一起转动，在光源的照射下，透过电码盘和光栅板形成忽明忽暗的光信号，光敏元件把此光信号转换成电信号，通过信号处理装置的整形，放大等处理后输出。输出的波形有六路：，其中是A，B，Z的取反信号。A,B两相的作用：根据脉冲的数目可得出被测轴的角位移，根据脉冲的频率可得出被测轴的转速，根据A，B两相的相位超前滞后关系可判断被测轴的旋转方向。Z相信号可实现被测轴的周向定位和旋转圈数计数。

1.2 数控机床运行状态数据采集卡的设计

数控机床运行状态数据采集卡的原理就是通过采集CNC伺服系统各轴交流电机光电编码器的信号来计算数控机床各轴的运行位移、速度和加速度等运行状态参量，并对这些运行状态参量进行误差分析和图形处理，判断数控机床的运行状况是否正常。

数控机床运行状态数据采集卡主要采用Atmel公司单片机AT89C55、计数芯片LS7266R1和CAN控制器SJA1000来实现，其系统原理图如图1所示。在图1中放大隔离用电压四差分比较器LM139实现，集成电路计数器用LS7266R1实现，中央处理器（CPU）采用单片机AT89C55，CAN控制器用Philips的SJA1000实现，光电隔离用6N137实现，CAN驱动器用PCA820C250实现。

图1 基于89C55单片机数控机床运行状态数据采集卡系统原理图

该数据采集卡主要实现对数控机床X轴和Y轴运行状态的采集，数控机床在运行过程中，其输出量如 XA+、XA-、XB+、XB-、YA+、YA-、YB+、YB- 等，经过LS7266R1采样、滤波、鉴相、倍频、计数等处理后，通过内部数据总线传递到现场级中央处理器（CPU）AT89C55，AT89C55对数据做出判断、计算、存储、打包等处理后，再通过内部数据总线传给CAN总线通信控制器SJA1000。如果总线忙，则等待；如果总线空闲，就通过CAN总线驱动器PCA82C250将信息发布到CAN总线上。

2 分布式数控机床远程测控系统数据分析处理方法

2.1 数据处理技术

数据处理技术是指用计算机收集、记录数据，经加工产生新的信息形式的技术。数据处理模块把采集回来的数据处理后，保存到PC机数据库中，通过对设备运行状态数据进行分析，判断设备运行是否正常。我们通常用的一些数据处理分析方法有最小二乘法、人工神经网络及小波分析等。本文主要介绍最小二乘法在数控机床各轴运行状态参量数据处理方面的应用。

2.2 X轴、Y轴平面内的圆弧插补运行状态分析

在X轴、Y轴平面内沿逆时针方向进行圆弧插补，运用数控机床运行状态数据采集卡对其进行实时性的数据采集，对光电编码器输出的信号进行滤波整形，鉴相倍频，提取整个动作的信号，同时对两路信号进行A/D转换，对脉冲进行计数，并通过计算得出接收到每个脉冲之后的X轴、Y轴位移：x1、x2、x3、x4…… xn；y1、y2、y3、y4…… yn，由 Vxn=xn+1-xn/T，Vνn=yn+1-yn/T（T=1/Nf，f为光电编码器的分辨率）可计算出X轴、Y轴的瞬时速度，把X轴、Y轴的瞬时速度和加速度绘制成图如图2所示。

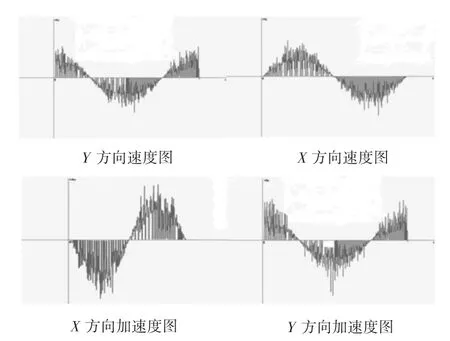
图2 X伺服轴和Y伺服轴的速度和加速度变

从图2中可以看出，机床的运行状态基本正常，但的确受到外界的干扰，通过对圆插补的运动信息进行滤波、误差分析，得到其在理想状态下的运动情况，以此来判断数控机床在不同负载下的运动状态是否正常。

2.3 最小二乘法滤波原理

最小二乘法通过最小化误差的平方和找到一组数据的最佳函数匹配，令误差之和为最小，通常用于曲线拟合。众所周知，过1个点可有无数条直线，过2个不同的点可求出唯一的一条直线，过3个不同的点不能求出一条直线。显然，过n(n>2)个不同的点(xi,yi)(i=1,2,3,…，n)能否求出一条直线的结论是否定的。在实际应用中，问题的提法降低为：能否求出一条回归方程。

可以近似地描述这些点的变化趋势就够了。自然地，(xi,yi)到直线（1）应满足点到直线的距离最短的条件。这使我们想起点到直线的距离公式

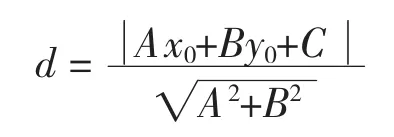
那么点(xi,yi)到直线（1）式的距离

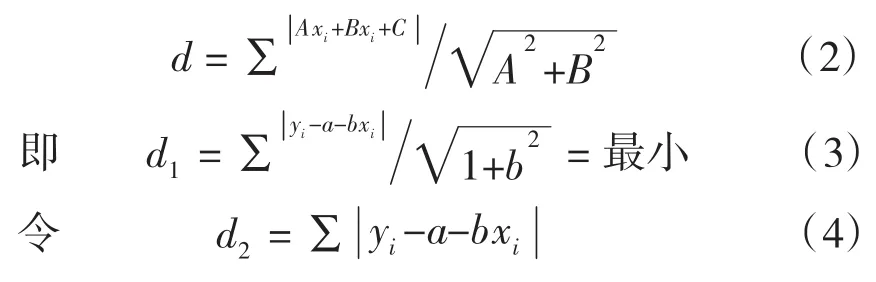
考虑（4）式的几何意义，它恰是(xi,yi)到直线（1）平行于Y轴的距离之和，两边平方，得：

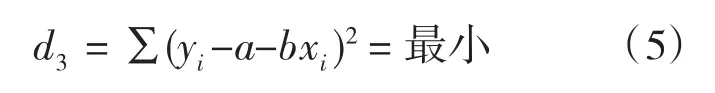
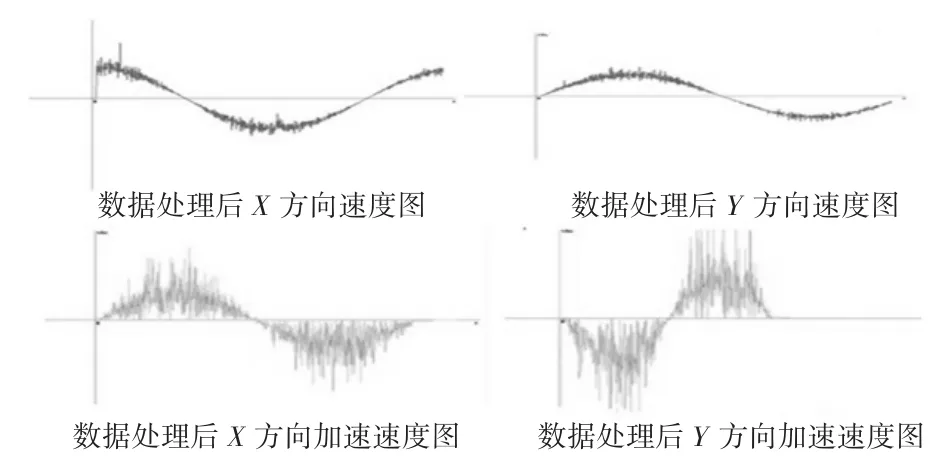
图3 经过最小二乘法处理后X伺服轴和Y伺服轴的速度和加速度变化图

当数控机床进行圆插补时，通过最小二乘法对采集的位移点和速度点进行曲线拟合，可以得出更加准确地位移图、速度图。通过最小二乘法进行数据处理后，X轴、Y轴的瞬时速度如图3所示变化。

2.4 理论分析

当机床工作在理想状态时，其误差应该是理论插补圆周（即内接多边形各边）上小范围的波动。当数控机床进行圆插补时，我们可以采集到X轴，Y轴的运动信息，画出其X轴和Y轴的速度和加速度变化图（图2），从图2中可以看出：X和Y工作台的运动速度和加速度在每一个瞬时均有急剧的速度和加速度毛刺，这是因为动力学系统只要速度发生变化，系统的震动是不可避免的。根据运动学分析，处于与坐标轴相交位置的各点，其两轴中必有一个轴的瞬时速度为零加速度最大，另一个轴的瞬时速度最大加速度最小，这时两轴的电机处于正反转临界点。从动力学的角度来看，由于速度和加速度的瞬变产生较大的惯性力，而在两轴插补的过程中，尽管X、Y两轴合成速度恒定，但X、Y轴的速度加速度分量都在不断改变，因此产生频率较高的瞬变的惯性力，导致同一时刻的两轴的受力状况不相同，结果引起实际插补产生许多较大的毛刺。经过最小二乘法滤波处理后，从X轴和Y轴的速度和加速度变化图（如图3）中可以看出，X、Y两轴的速度和加速度图毛刺减小，部分干扰信号消除，图形得到较大程度的还原。

3 结束语

本文在数控系统实验平台下对圆弧插补的轨迹进行位移数据的采集，计算出X轴和Y轴的瞬时速度和加速度，利用最小二乘法对瞬时速度和加速度进行数据处理滤波，去除外部干扰，绘制出准确的瞬时速度和加速度图，可依此对数控机床的运行状态做出一个客观、公正的评价。这种检测数控机床运行状态的方法也可以用于直线插补、螺纹加工及任意组合运动轨迹，还能判断三轴和多轴数控机床的运行状态。

[1]黎亚元，肖继学，陈守强.数控系统圆插补误差测试及分析[J].黑龙江工程学院学报.2001(9):48-52.

[2]陈金成，徐志明，钟进修等.机沐沿曲线高速加工时的运动学与动力学特性分析[J].机械工程学报.2002(1):31-34.

[3]韩兴国，黎亚元.基于分布式数控机床远程监控系统研究[J].桂林航天工业高等专科学报.2009(4)：26-29.

[4]廖效果，朱启逑.数字控制机床[M].武汉：华中科技大学出版社，2003.