神经模糊PID控制算法在恒压供水系统中的应用

谢 静

(陕西工业职业技术学院 电气工程学院，陕西 咸阳 712000)

0 引言

恒压供水系统的实际工作过程会不断受到随机因素的干扰，并且该系统还具有大惯性、非线性、纯滞后性、参数时变等特点，因此，难以用精确的数学模型描述.当水泵运行在变频电源与工频电源的切换状态时，压力由连续状态变为波动状态，此时系统等效于受到了严重的阶跃干扰，若采用传统的PID控制进行控制，不仅调节时间长，而且还可能出现严重的超调和振荡[1].

本文以某市供水厂的供水情况为研究背景，以微处理器和变频器为主要单元组成变频恒压供水系统，实现对供水压力的实时控制，使管网水压稳定在设定值.为了提高供水管网压力的控制精度，使系统能够长期稳定运行并具有较强的适应能力，尝试采用智能控制算法对变频恒压供水系统进行实时控制，研究控制算法对系统性能的影响，以优化控制算法[2].

1 变频调速恒压供水系统结构

1.1 变频调速恒压供水系统

整个供水系统主要由变频调速器、神经模糊PID控制器、压力变送器、水位控制器以及接触器、继电器、指示灯、风机等组成.系统的主要任务是利用恒压控制单元使变频器对水泵M5进行无极平滑调速，对M1-M4进行工频控制，利用压力信号来控制变频器以实现水泵电机的运行，保证管网压力的恒定.这种控制方法即可以解决供水高峰时水压不足的问题，又可以解决深夜用水低谷时水压过高且浪费资源的问题，以达到节约能源的目的[3].

1.2 恒压控制原理

本系统包括5台水泵电动机，其中M1的功率为45kW，M2为22kW，M3为22kW，M4为22kW，M5为160kW.M1-M4四个电机用一般的工频电源，M5由变频器控制，以实现变频调速，并且M5电机可以实现工频/变频转换.变频器采用富士变频器，其型号为FRN160PS-4JE.根据春夏秋冬四季用水量和一天24小时用水量的变化规律，将供水压力分为：3.0Kgf/cm2、3.5Kgf/cm2、4.0Kgf/cm2、4.5Kgf/cm2和5.0Kgf/cm2五个档，在不同的时间断，采用不同的供水水压，以达到充分节能的目的.图1展示了恒压供水系统的结构框图.

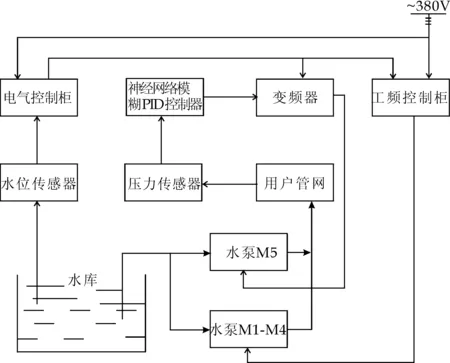
图1 变频器恒压供水系统框图

系统的控制过程为:通过安装在用户管网端的压力传感器测得管网水压的变化，根据城市用户管网在不同时刻对水流量的需求，以及管网水压的变化，将测得的水压信号传至神经网络模糊PID控制器，经过控制器运算后将信号输入变频器，由变频器最终完成对水泵转速的控制，从而达到调整管网水压的目的[4].

2 神经模糊PID控制原理及参数整定模型

2.1 神经模糊PID控制原理

与传统PID控制相比，模糊控制具有很多优点.模糊控制是建立在模糊数学基础上的一种智能控制技术，可以达到传统控制策略无法达到的效果.模糊控制能较好得跟随系统状态的变化动态调整自身控制参数，不需要建立精确的控制对象模型，因而在实际中的应用越来越广泛.但模糊控制也存在固有的缺点：通常情况下，设计完成的模糊控制器的语言规则和合成规则往往是不可调整的，而实际系统的参数是变化的，用这样的模糊控制表去控制实际系统，很难达到满意的控制效果.神经网络采用某种网络拓扑可以描述任意的非线性函数，并且具有学习能力和记忆能力，同时在一定程度上可以模仿人脑神经系统的信息储存能力和处理能力，具有很强的自学习自修正能力，使其对供水系统的模糊PID控制策略进行自调整，在模糊控制中引入自修正因子，可以实现控制系统的自适应能力，满足系统要求[5].基于此本文提出了一种新型控制策略——神经模糊PID控制算法，该算法综合了以上各算法的优点，它不仅具有神经网络控制的自学习自组织能力，还具有模糊控制的鲁棒性强、适应性强的优点，另外还拥有PID控制的实现简单方便等优点[6]，优于以往的算法.图2显示了神经网络模糊PID控制器的结构框图，该控制器由三部分组成：

(1)神经网络控制器：控制模糊规则的动态调整，通过神经网络的自学习，使模糊规则的生成转变为加权系数的确定和调节.根据供水系统的运行状态，调节PID控制器参数，使供水系统最终达到最优控制.

(2)模糊控制器：对系统的输入输出变量进行模糊化和归一化运算.这些运算的意义是鉴于模糊控制的强鲁棒性和非线性控制作用，对输入到神经网络的模糊规则进行预处理，避免了神经网络采用sigmoid激活函数时，由于输入过大而导致输出饱和.

(3)传统PID控制器：直接对供水系统的控制过程进行闭环控制，并且对3个参数KP、KI、KD实行在线调节，使控制作用时刻跟踪系统的变化.

图2 神经网络模糊PID控制器结构框图

从下图中可以看到：使输出层神经元的输出状态与PID控制器的kp、ki、kd参数相对应，从而通过神经网络的自学习能力实现加权系数调整，进而使其稳定状态与PID的最优控制相对应，最终利用PID控制器的输出u来实现对供水系统的水压的控制[7].

2.2 神经模糊PID参数整定模型

神经模糊控制器的核心是建立恰当的模糊控制规则并分别针对KP、KI和KD进行整定模糊规则表[8].

在不同的|e|及|ec|下，被控过程对参数kp、ki和kd的自整定要求可归结如下[9,10]：

(1)当|e|较大时，不论误差变化趋势如何，都应考虑控制器的输出按最大(或最小)输出，以达到迅速调整误差，使误差绝对值以最大速度减小，同时为了防止积分饱和，应取较大kp，较小kd，ki为零.

(2)当e*ec>0时，说明误差在朝着绝对值增大的方向变化.此时，若误差较大，可考虑由控制器实施较强的控制作用，以达到扭转误差绝对值朝减小方向变化，并迅速减小误差绝对值；此时取较大的kp，kd不能太大，取较小的ki值.若误差绝对值较小，控制器实施一般的控制作用，只有扭转误差的变化趋势，使其朝误差绝对值减小的方向变化.

(3)当e*ec<0，或者e=0时，说明误差绝对值朝减小的方向变化，或者已达到平衡状态，此时可采取保持控制器输出不变.

(4)当e*ec=0，e≠0时，表明系统的曲线与理论曲线平行或一致.为使系统具有良好的稳态性能，应采取较大的kp和ki值，同时避免设定值附近振荡，并考虑系统的抗干扰性能，选取适当kd值.

根据上述原则及专家经验，可以列出kp、ki和kd的控制规则表，如表1～3所示.

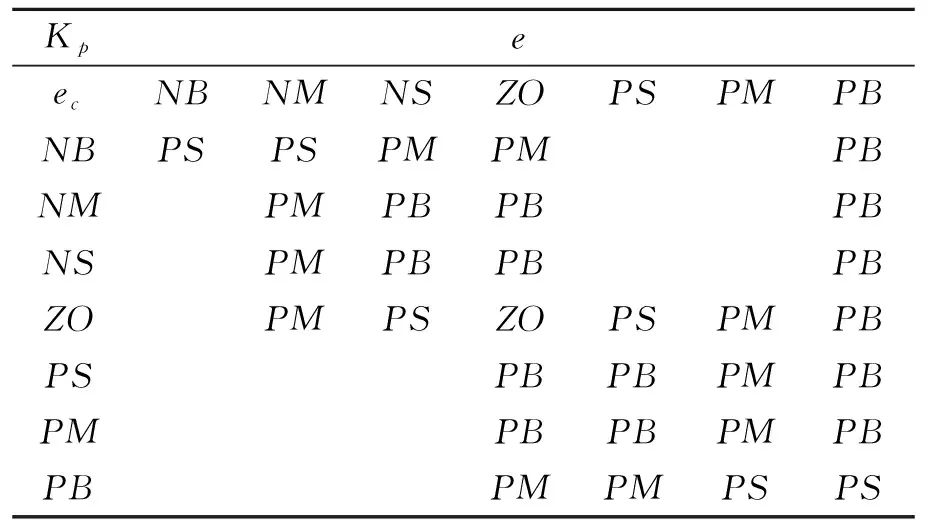
表1 参数KP调节规则表

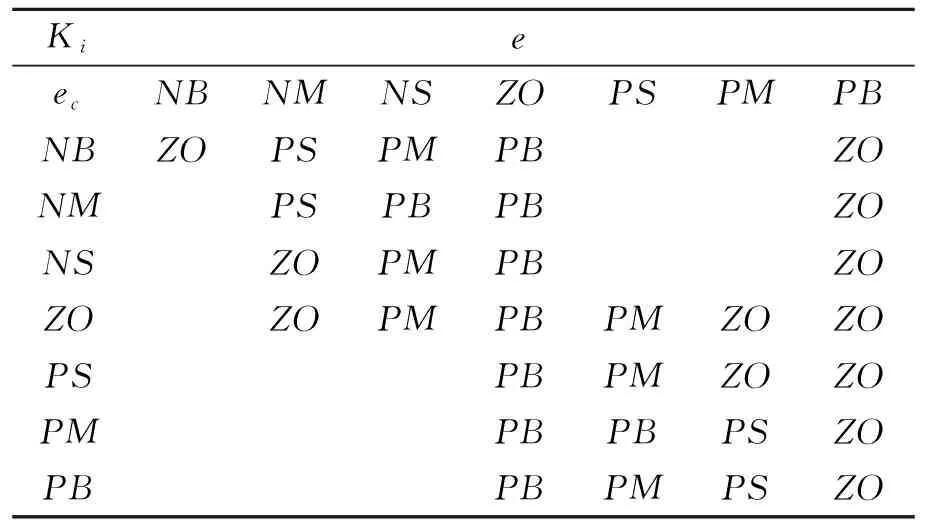
表2 参数KI调节规则表

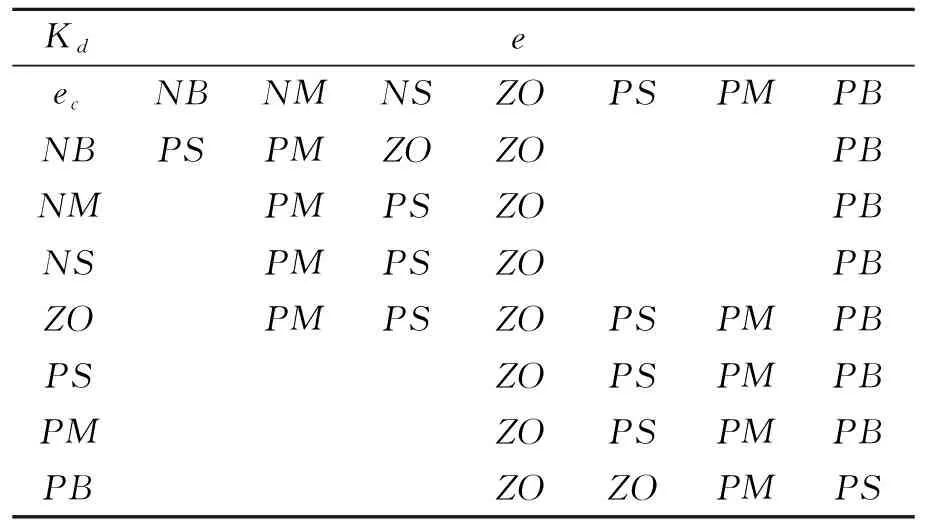
表3 参数KD调节规则表

3 神经网络模糊PID控制算法

模糊控制模块的作用是将系统的状态变量{e(k),de(k)/dt}进行模糊化、归一化处理，即根据输入变量模糊子集的隶属度函数将输入的数值归一化到各自的隶属度.

本文将模糊控制器的语言变量分为7个：{NB,NM,NS,ZO,PS,PM,PB}，分别表示{负大，负中，负小，零，正小，正中，正大}.在隶属度函数的选择上采用三角函数.同时在ZO附近将隶属度函数的陡度取得较大些，其目的是为了提高隶属度函数的分辨率，进而增强供水系统鲁棒性.采用BP神经网络[11]进行设计，采用三层网络设计，输入节点数目为4个，隐含节点数目为8个，输出节点数目为3个.将模糊处理后的系统状态变量作为神经网络的输入，而PID控制器的3个可调参数kP、ki、kd为神经网络的输出.由于PID控制的参数不能为负，因此宜将控制神经网络输出的函数取为非负的sigmoid函数，隐含层可用正负对称的sigmoid函数.将模糊处理后的系统状态变量作为神经网络的输入，而PID控制器的3个可调参数kP、ki、kd为神经网络的输出[12].

用微机实现神经模糊PID控制算法，本文的供水系统采用的是经典增量式数字PID控制[13]，控制策略为：

u(k)=u(k-1)+KP[e(k)-e(k-1)]

+KIe(k)+KD[e(k)-2e(k-1)+e(k-2)] (1)

式中kP、kI、kD——比例、积分、微分系数，u(k)是控制器的输出，通过u(k)来控制供水系统的水压[14].

4 控制算法的MATLAB仿真研究

选取纯滞后一阶惯性模型如下：

(2)

针对供水系统的参数K,T,τ变化时的阶跃响应进行仿真比较，对本文提出的神经网络模糊PID算法与以上控制算法的性能特性进行对比[15].分别使令K∈(1.5,2)、T∈(20,30) s、τ∈(8,12) s等参数进行仿真比较；并且当K=1.5、T=20 s、τ=8 s参数条件下加入幅值为10～20%的随机二元信号为干扰信号，以比较抗干扰性.系统响应如图3和图4所示.

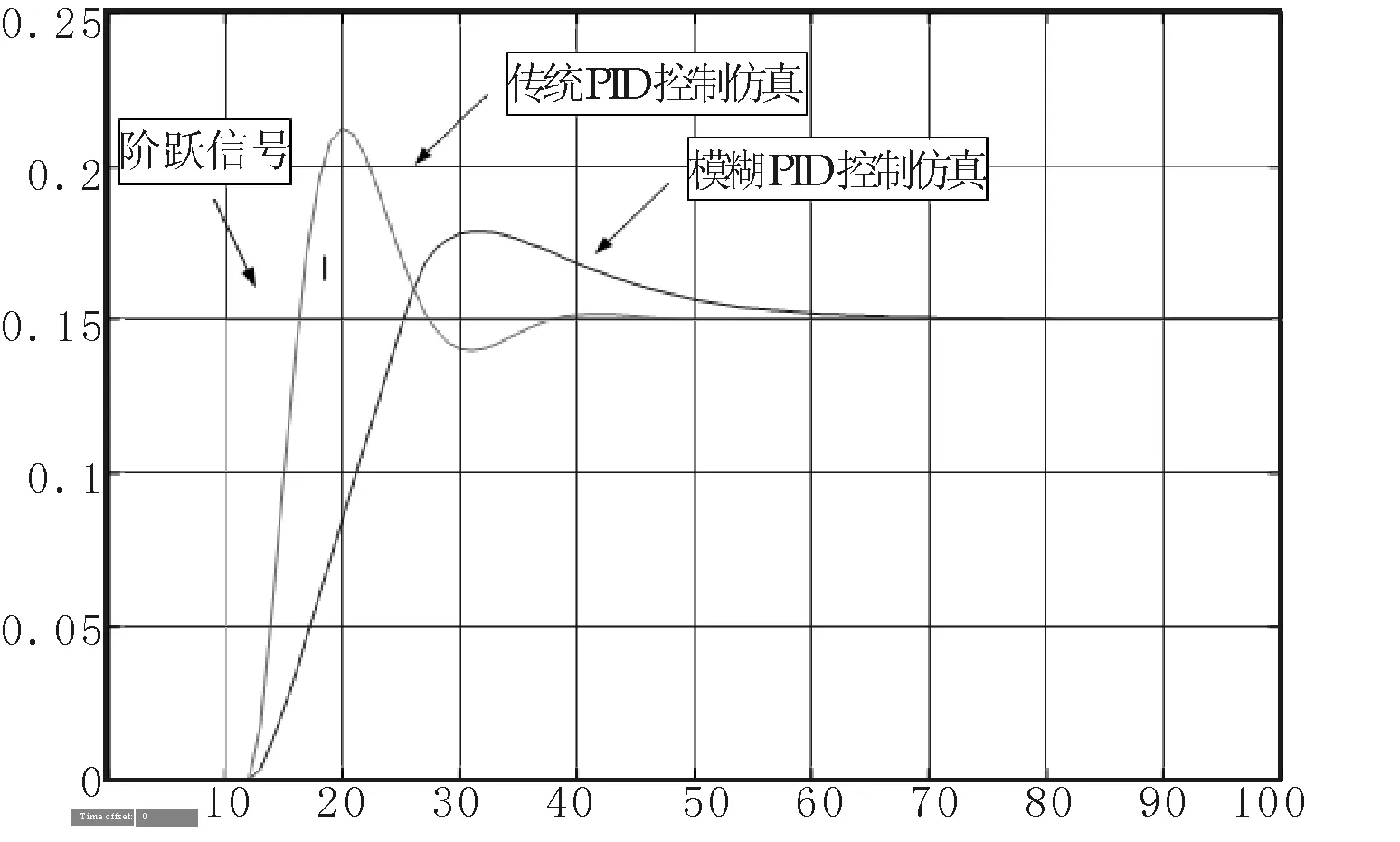
图3 传统PID控制和模糊PID控制仿真对比

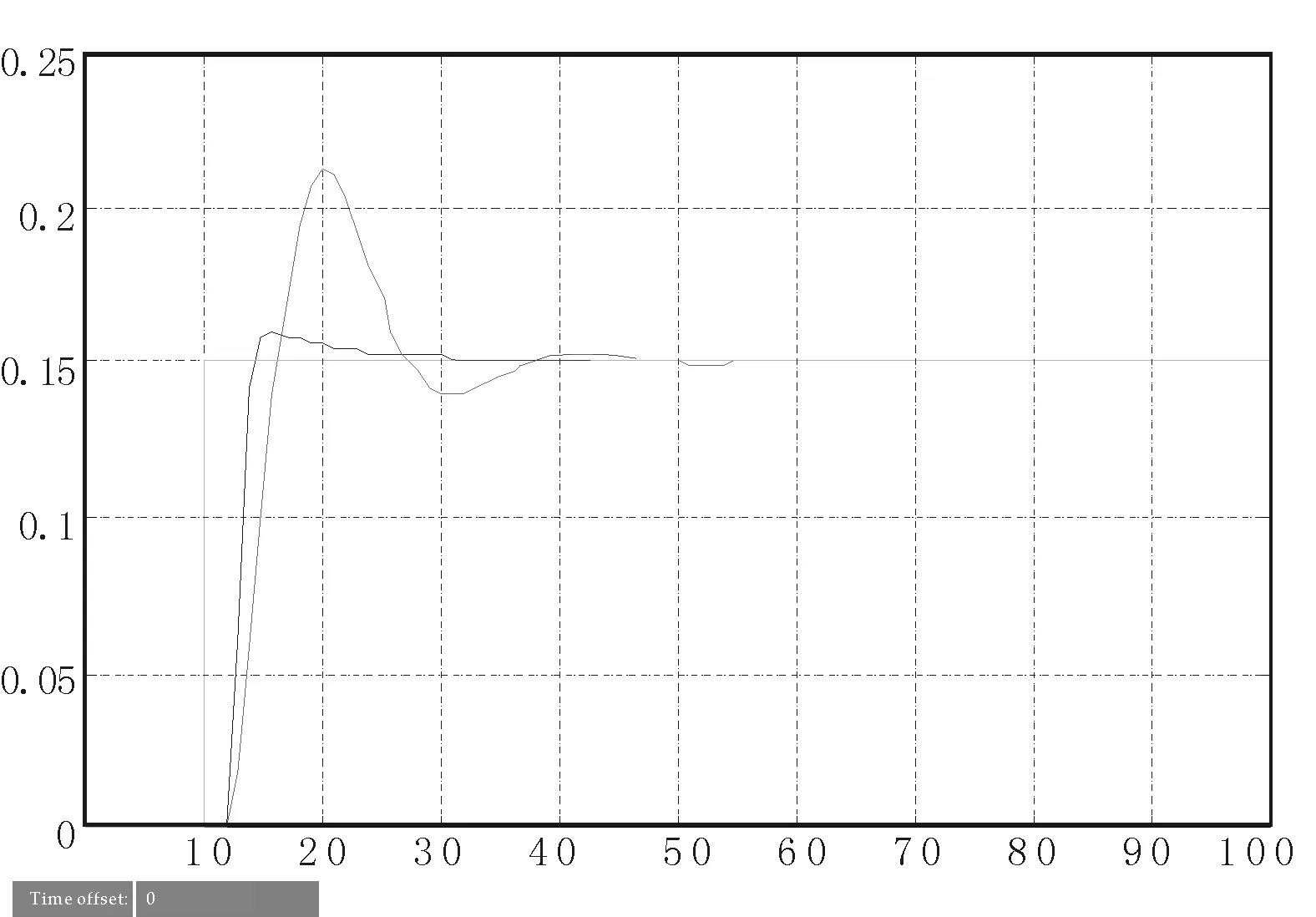
图4 传统PID控制和神经网络模糊PID控制仿真对比

在10 s时给系统施加幅值为0.15的阶跃信号作用于上图所示的各系统仿真图中.可以看到：传统PID控制算法的响应第一次超调超过0.21，约为40%，超调相当大不利于系统稳定，上升时间为8 s，也比较长；模糊PID控制算法的响应超调约为0.18，约为20%，超调不太大而且只有一次超调且未发生多次振荡，较为遗憾的是该控制算法的上升时间为22 s，时间过长，当系统状态发生变化时不利于系统再次恢复正常状态运行；神经网络模糊PID控制算法的响应超调约为0.16，约为6.7%，超调控制的相当好，上升时间为仅为3 s，时间很短，这表明即使系统状态发生变化也能很快恢复正常.通过对比可见模糊PID控制算法虽然有利于抑制超调但是上升时间过长，而神经网络模糊PID控制算法不仅能够进一步减少超调并且可以控制上升时间到很小的程度.

5 结束语

神经模糊PID控制算法是综合了神经网络控制、模糊控制和PID控制的优点的控制算法，该算法能够自适应的计算模糊规则，并且具备鲁棒性强，适于非线性控制等优点，该算法能够很好的应用于恒压供水系统.在此基础上进行的MATLAB仿真结果表明神经网络模糊PID控制算法在恒压供水系统中的效果较之传统PID控制和模糊PID控制具有较好的控制性能.

[1] 乔维德.基于模糊控制的恒压供水系统研究[J].水科学与工程技术，2007，31(4):28-30.

[2] 钟 珞,饶文碧,邹承明.人工神经网络及其融合应用技术[M].北京：科学出版社，2007.

[3] Zou A.p. Energy-saving design for frequency control and constant. pressure water supply system in residential area[J].China Water and Wastewater,2003, 9(8):76-78.

[4] 范力旻.双闭环恒压供水系统[J].应用能源技术,2006,23(11):36-38.

[5] 胡宝清.模糊理论基础[M].武汉:武汉大学出版社,2004.

[6] SooYeong Yi, Myung Jin Chung. System design and stability analysis of a fuzzy logic controller[J].Fuzzy Set and System, 2003, 271-298.

[7] 叶少珍.基于神经网络的模糊控制系统的研究[J].福州大学学报(自然科学版), 2006, 28(3):98-101.

[8]李友善,李 军.模糊控制理论及其在过程控制中的应用[M].北京:国防工业出版社,2003.

[9]张智星,孙春在.神经-模糊和软计算[M].西安:西安交通大学出版社,2002.

[10]谢仕宏,朱晓聪.模糊PID控制算法在恒压供水系统中的应用[J].陕西科技大学学报,2007, 25(2)：109-112.

[11]A.Blanco, M.Deigado, I.Requena. Improved fuzzy neural networks for solving relational equation[J]. Fuzzy Set and System, 2002：311-322.

[12]王孟效,孙 瑜，汤 伟，等. 制浆造纸过程测控系统及工程[M]. 北京: 化学工业出版社,2003.

[13]Eker,Lyas.Operation and control of a water supply system[J].ISA Transactions,2003, 2(3)：461-473.

[14]李臣明，张邦楚，韩子鹏，等.BIT导弹模糊自适应PID控制[J]. 弹箭与制导学报,2005, 25(2):487-490.

[15]张志涌，徐彦琴.MATLAB教程-基于6.x版本[M] .北京：北京航天航空大学出版社,2001.