基于加工中心的极小子样试验评估法

杨志伟， 任工昌， 孟勃敏

(陕西科技大学机电工程学院， 陕西 西安 710021)

0 引 言

根据传统经典的可靠性试验分析理论，试验测试所得的样本量越大，试验评估的精确度就越高，但是如果试验对象是大型复杂的，则试验成本极其昂贵.另外对于批量较小的机构产品进行较大的样本量(样本量n≥10)的试验，在财力上也是难以接受的.尤其是昂贵的高可靠性产品，可靠性试验往往只能是n=1或n=2的极小样本，因此对高可靠性极小子样本的可靠性评估具有重大的应用价值[1].为了进一步解决工程上较多出现的试验样本数为1～2的场合下的可靠性评估问题，本文以某机床厂生产的加工中心为研究对象，提出了将虚拟增广法和半经验评估法相结合的新的评估精度更高的可靠性评估方法，并对加工中心进行了试验寿命的可靠性评估.

1 半经验评估方法的阐述

半经验评估方法是充分利用过去的大量工程试验的经验信息(包括类似件试验)，依据现场试验数据，根据数理统计和可靠性评估理论对数据进行分析处理，得到一个在一定误差范围内满足工程实际需要的评估结果.

基于大量的数据统计工程试验经验得到有关加工中心的信息是：

(1) 加工中心的性能退化轨迹服从Weibull分布；

(2) 美国波音公司通过对大量的Weibull分布试验数据的统计分析，给出了Weibull分布形状参数β，结果如下[2，3]：

对于铝合金结构，β0=4；对于钛合金结构，β0=3；对于钢结构，β0=2.2.

根据大量的工程实际经验，产品寿命既近似服从对数正态分布，又近似服从Weibull分布.因此，对数寿命标准差σ与Weibull分布形状参数β之间存在如下关系：

(1)

由上述公式可知：对数寿命标准差σ是随Weibull分布形状参数β增大而减小的，反之亦然.假设Weibull分布形状参数β已知，则可通过上述公式计算出服从对数正态分布的对数寿命标准差σ的值，即将服从Weibull分布的寿命评估计算转换成服从对数正态分布的寿命评估计算.

2 半经验评估方法的数学描述

(2)

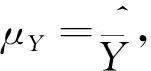
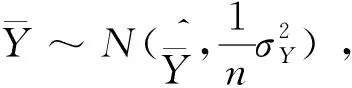
(3)

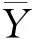
(4)

从而得到产品试验寿命的100(1-α)%置信下限为：

(5)

3 虚拟增广样本方法

根据抽样理论，试验样本量越大，可靠性评估的准确度越高，越能够真实地反映产品的可靠性水平.虚拟增广样本法即为根据原始试验样本均值Y0以及以往类似件试验估计得到的分布形式和标准差.为了使得虚拟增广后的新子样所蕴含的随机特性与原子样的随机特性的差别在工程允许范围内，虚拟增广的过程需要满足以下两个基本条件(虚拟增广样本方法的立论依据)：虚拟增广后的子样均值应与原来的子样均值相等，且虚拟增广后的子样标准差应与类似件的子样标准差相等[6].

当原始样本量为n=1，把试件的样本量从n=1虚拟增广到n=10，假设类似件试验估计得到的分布形式为正态分布(标准差σ假设已知)，为使虚拟增广得到的样本更合理，建议用以下近似经验公式虚拟增广原始样本：

Y=Y0±[0.106×(i-1)2+c]σi=1,2,3,4

(6)

式中Y0(当原始试验样本量为1时，只能近似地取Y0=Y*，Y*为一次试验的样本值)为原始样本均值，σ为类似件的标准差，Y为虚拟增广后得到的样本值，c是为了满足立论依据的限制条件而待定的常数系数.

建立在原有样本点Y*的基础上虚拟增广至10个样本点，按公式(6)的方法增广后的样本为：

Y1=Y0-(0.106×42+c)σ;Y2=Y0-(0.106×32+c)σ;Y3=Y0-(0.106×22+c)σ;Y4=Y0-(0.106+c)σ;Y5=Y0-cσ;Y6=Y0+cσ;Y7=Y0+(0.106+c)σ;Y8=Y0+(0.106×22+c)σ;Y9=Y0+(0.106×32+c)σ;Y10=Y0+(0.106×42+c)σ.

根据虚拟增广的理论依据，应有如下方程组(7)、(8)：

(7)

(8)

根据方程组(7)、(8)可求解得到c=0.079 8，将c代入Y1，Y2，…,Y10的表达式，即可得到由n=1虚拟增广至n=10后的样本分别为：(Y0-1.775 8σ)，(Y0-1.033 8σ)，(Y0-0.503 8σ)，(Y0-0.105 8σ)，(Y0-0.079 8σ)，(Y0+0.079 8σ)，(Y0+0.185 8σ)，(Y0+0.503 8σ)，(Y0+1.033 8σ)，(Y0+1.775 8σ).

4 加工中心的可靠性评估

对某加工中心结构作一次寿命试验，得出其伪失效寿命为T0=972 h，由大量的数据统计经验可知加工中心的结构寿命T是一个服从Weibull分布的随机变量.根据美国波音公司对大量的Weibull分布试验数据的统计分析，对于钢结构，从保守角度考虑，加工中心的性能退化轨迹的Weibull分布形状参数β一般取2.2，将此数据代入式(1)中，再通过查表，计算出服从对数正态分布的对数寿命标准差σ的值为0.197 7，在90%的置信度下对加工中心进行可靠性评估.

根据前面所述的半经验可靠性评估方法易知，置信度为100(1-α)%=90%时，加工中心平均无故障试验寿命的置信下限为：

(9)

5 结 论

根据所建立的产品对数寿命标准差σ与Weibull分布形状参数β之间的关系式，利用加工中心性能退化轨迹服从Weibull分布的形状参数β值确定了对数寿命标准差σ值.在加工中心试验样本量n=1，很难做出较准确的试验评估的情形下，本文提出的将虚拟增广法与半经验评估法相结合的新的可靠性评估方法评估精度更高更合理，能够更加准确地对加工中心进行平均无故障寿命评估.

参考文献

[1] 冯蕴雯，黄 玮，吕震宇，等.极小子样试验的半经验评估方法[J].航空学报，2004,25(5)：456-459.

[2] 傅惠民，岳晓蕊，张勇波.极少失效数据的可靠性评估和寿命预测[J].航空动力学报，2010，25(8)：1 855-1 858.

[3] 傅惠民，王凭慧.无失效数据的可靠性评估和寿命预测[J].机械强度,2004，26(3)：260-264.

[4] 方 亚.机械产品可靠性评估方法研究[D].西安：西北工业大学硕士学位论文，2007.

[5] 田 远.极小子样可靠性评估方法研究及在C70型敝车中枕梁结构评估中的应用[D].北京：北京交通大学硕士学位论文，2008.

[6] 黄 玮.机构可靠性分析方法研究[D].西安：西北工业大学硕士学位论文，2005.