基于加热法的蒸汽湿度在线测量装置研究

姜 浩，张美凤，李 勇，钱江波，相明辉，史萌萌

0 引言

湿蒸汽两相流广泛存在于自然界和工程领域，在电力和动力工程中，湿蒸汽两相流动问题随冷凝式汽轮机的出现而出现。火电厂凝汽式汽轮机低压缸及核电站饱和式汽轮机中往往会出现湿蒸汽两相流，而由此带来的损失十分可观。在英国，仅由于透平中湿度引起的效率降低而带来的经济损失每年达5 000万英镑［1～3］。在蒸汽透平中湿蒸汽主要带来两方面的问题，一是蒸汽凝结产生的水分或湿蒸汽进入透平带入的水分使机组效率降低;二是湿蒸汽中的水滴会导致透平低压级组动叶片的水蚀损坏［4］。

汽轮机排汽湿度的准确在线测量，有助于确定湿蒸汽区级的工作状态，确定级效率，为汽轮机安全经济运行以及汽轮机的优化设计、结构改进提供依据，其理论意义和实用价值显著。

近几十年来蒸汽湿度测量技术的研究越来越受重视，根据湿蒸汽的不同物理特性，研究出了不同的蒸汽湿度测量方法［5～17］，但到目前为止没有一个可以用于实际生产中。本文主要分析湿度测量的原理和能量损失，研究基于加热法缸内测量汽轮机排汽湿度的装置，分析湿度测量的误差。

1 加热法缸内测量蒸汽湿度原理

加热法缸内测量蒸汽湿度原理:在汽轮机末级缸内将湿蒸汽加热成过热蒸汽，通过测量装置出口温度和压力确定出口焓值，通过功率表测量加热器输给铜管的热量，从而计算焓差值，确定抽入测量装置的湿蒸汽的焓值。如图1 为汽轮机缸内测量蒸汽湿度工作原理简图。取样时，将探针头部伸入汽轮机末级后排汽口处，湿蒸汽流自由通过加热管圈吸收热量，加热成过热蒸汽，通过流量调节阀控制取样流量，采用真空泵维持测量装置的压差，乏汽排向汽轮机凝汽器。

被抽取的具有代表性的湿蒸汽试样质量、压力、湿度和速度分别为m，P0，Y，U0，在加热段中被加热到干饱和状态或者过热状态，加热后的状态参数为压力p1、温度T1，加热元件产生的热量为Q，散热损失量为q。根据加热段的能量守恒关系式:

图1 加热法缸内测量汽轮机蒸汽湿度工作原理图Fig．1 Work schematic for heating cylinder measurement of the turbine steam humidity

式中:出口段的焓值h1可以根据压力p1和温度T1确定，输入的热量Q 根据功率表测定，在忽略工作段前后速度变化时，工作段的进口焓h0通过式(2)计算求出:

因此，工作段进口的湿度可以按压力P0和焓值h0在焓—熵图上确定，余下的问题就是如何确定质量流量m 和散热量q。由于散热损失的精确测量非常困难，是造成湿度测量困难的主要原因之一。因此试验中必须减少热损失来提高测量精确度。进一步将式(2)写成:

该式反映了用加热法测量湿度的原理，即通过测得加热后蒸汽焓值、进口汽流压力以及加热量来间接求出进口汽流湿度值。

流体在管内的流动状态影响整个测湿装置设计，流体流动状态稳定程度不仅决定测量能否实现，且影响测量的准确性。所以对于设计和优化测湿装置，装置进出口两端的压差选择具有重要意义。

在汽轮机排汽湿度的数值计算中，作如下简化假设:第一，假设流体为不可压流体，忽略液滴和蒸汽之间的速度滑移;第二，忽略液滴和蒸汽之间的作用力;第三凝结相即液相，所占的质量份额较小;第四，液滴所占的体积份额不予考虑。

2 典型工况下装置蒸发段的数值模拟结果

由于测量装置较复杂，为方便计算，将原装置图分成5 部分分别模拟:(1)装置最前面的部分，即细管; (2)加热器的核心部分，即螺旋管;(3)细管变成粗管的部分为变管;(4)粗管弯曲的部分，即弯管; (5)装置最后的一部分，即粗管。

汽轮机稳定运行时，其入口和出口边界条件可以唯一确定。用FLUENT 模拟时，假设汽轮机末级蒸汽压力为7 kPa，为不可压流体，温度为饱和温度，采用自由出口，分别计算不同入口速度50 m/s， 70 m/s， 90 m/s， 110 m/s， 130 m/s，150 m/s，170 m/s，190 m/s，对 应 的 压 损 如 表1所示。

表1 不同入口速度的压损Tab．1 Pressure loss in the entrance of different speedsPa

表1 中，为了计算方便，入口的细直管取0.5 m，螺旋管取3 圈，变管(细管变粗管)粗管取0.2 m，弯管(粗管弯曲的部分)前后各取0.2 m，粗直管取0.5 m。

由表1 可知，一定流速下，变管、螺旋管压损较大。当入口的速度为190 m/s时，变管和螺旋管压损超过20 kPa，即使在装置中加入真空泵也无法使汽轮机内的湿蒸汽稳定的流入测湿装置，所以此种装置设计在实际中功能无法实现。

3 改进型测湿装置模型及数值模拟

3.1 改进型测湿装置模型

考虑到上面的模型中压损过大主要是由于管道过细且存在变直径管道，新方案拟加大模型中管子的内径、减少弯管，即将管的内径由原来6 mm改为18 mm，将螺旋管的直径由原来的45 mm增大至200 mm，同时为了减少管子弯头造成较大的压损，螺旋管和直管的连接处采用光滑过渡连接，而且直管和螺旋管的内径都为18 mm，由此设计出两种装置模型，如图2，3 所示。

汽轮机末级湿蒸汽流入内径为6 mm的探针，经过一段稳定管，其内径扩大为18 mm，再加热为过热蒸汽，最后排出。在装置的末端设置流量调节阀，通过调节流量以实现稳定流动。流入探针的湿蒸汽的压力、湿度、流量、密度分别为P0，Y，D0，ρ，过热蒸汽的状态参数为压力P1、温度T1。图2 中，通过测量过热蒸汽的温度T1和压力P1，查焓熵图得出过热蒸汽的焓值，对湿蒸汽输入的热量为P，损失的热量为q。能量平衡方程为

湿蒸汽是由饱和汽和饱和水组成，其湿度计算如下:

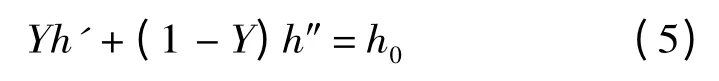
式中:h'，h″分别为饱和水和饱和蒸汽焓。

图3 中:

(1)给定Y0初值。

(2)可测入口气体的流速(无滑移)，液滴速度也为c0，压力P0，入口截面积A0已知，计算湿蒸汽密度ρ0，则湿蒸汽的流量:

(3)调节流量计后阀门，使流量达到D0。

(4)按照式(5)计算出流动湿蒸汽的湿度Y。

(5)比较Y0和Y 差值，重新设定Y0重复上面的计算，直到计算结果和设定值相同为止。

在两种湿度测量中，散热损失会造成湿度测量不准确，因此必须减小热损失来提高测量精度。该装置为了减少热量散失，用双层真空的装置将加热器与外界隔绝，并在装置内部涂上高表面辐射系数的涂层，进一步减少散热损失。

3.2 典型工况的数值模拟分析

根据做好的网格模型，用FLUENT 软件进行三维管中的数值模拟，汽轮机排汽末级压力为7 kPa，物性为不可压流体，温度为饱和温度，采用自由出口，蒸汽入口速度为70 m/s，100 m/s，130 m/s，160 m/s，190 m/s时结果如图4 所示。

图4 不同流速下管道压损Fig．4 Pipeline pressure loss at various flow rates

由图4 可以得出整个测湿装置中始末两端的压差随湿蒸汽在管道内的流速的变化曲线，结果如图5 所示。由图5 可知，当管道内的流速增加时，探针内压损也是呈递增趋势，且在流速最大200 m/s时管道内的压损小于2 kPa，可以不使用真空泵，设计出探针加热段的长度大于水滴的汽化长度，使得湿蒸汽稳定进入探针内。

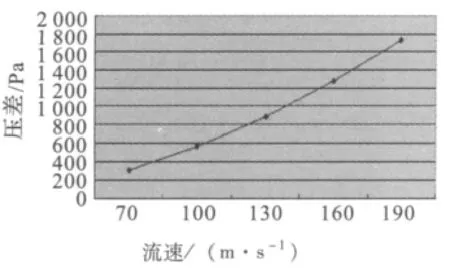
图5 流体流速与管道内压损的对应关系Fig．5 Corresponding relationship between fluid flow and pipeline pressure loss

4 能量损失分析和湿度误差分析

4.1 加热段向非加热段导热的热量损失分析

由于加热段较外铜管温度高，所以加热段的铜管向探针探头方向存在热传导，为了减少热传导散热量，在加热段和探针探头之间加装导热系数低的瓷管以减少热量散失。本文以特定工况(p=5 kPa，Y =0.15，过热度△T =20 ℃)的热量损失估算装置的散热量。

已知压力和湿度，根据焓熵图可以得出饱和水的密度ρ'和饱和蒸汽的密度分别为ρ″，饱和水的 温 度 t0，其 中:ρ' = 994.792 kg/m3，ρ″ =0.035 468 kg/m3， t0= 32.91 ℃， h0=2 198.04 kJ/kg，得出湿蒸汽的密度为ρ ==0.041 74 kg/m3，将该湿蒸汽加热到过热度为20 ℃的过热蒸汽，查表可知过热蒸汽的焓值h1=2 597 kJ/kg，Δh=h1－h0=399 kJ/kg，由流量公式D0=C0A0ρ0，可以得到通过加热段的流量:D0=0.000 210 949 kg/s，则需要加热成过热蒸汽需要的热量Q0=D0×Δh=0.084 1 kW。

管和水蒸气的对流换热是通过铜管与蒸汽之间的对流换热来实现的，计算过程如下:水蒸气的平均温度tf==42.91 ℃，以此为定性温度，查表可知vf= 168 × 10－6m2/s，Prf= 0.887，λf=2.08 × 10－2W/(m·k)，由此可得到雷诺数Ref== 2 142 ＞2 000，流动为湍流。则根据Nuf=0.023 RPr，代入数据可得出Nuf=10.128，表面传热系数:

代入数据可得出:hm=11.703，根据对流换热速率公式Q=AhΔt，可知铜管与水蒸气的温差Δt =33.77 ℃，即加热段的始端的铜管的管壁温度t'1=66.68 ℃。

计算铜管内的导热:瓷管的长度为0.1 m，外径为0.03 m (假设通过热传导传过瓷管的热量全部被汽轮机的蒸汽带走，及瓷管温度与汽轮机内蒸汽温度相同)。

已知瓷管的导热系数λ =1.1 W/(m·k)，由导热定律:

得到导热损失的热量φ=0.145 8 J。

铜管的向外的辐射散热分析:由于铜管温度较高，存在辐射散热，由上面的计算可知铜管的平均温度为tw铜=76.68 ℃，根据斯忒藩—波尔兹曼定律:

计算铜管在没有防辐射涂层时的辐射力E =678.19 W/m2，辐射热损失Q' =E·S=144.43 W。

由于涂有防辐射涂层，防辐射效率超过99.9 %，可知实际辐射损失的热量为Q=0.144 W。

综上计算得出热量损失率

4.2 湿度误差分析

由于流动蒸汽湿度测量迄今为止没有标准的校准装置，因此，测量误差只能通过分析有关的热力学参数得到。根据间接测量湿度的计算式(3)，采用均方根误差公式，通过每一个相关变量的精确度求出湿度均方根差。根据测量仪表的精度，得出各个被测量的相关参数误差如下:压力ep= 0.002;温度eY= 0.002 5;质量流量em=0.002 5;加热功率eQ=0.001。

由于内管加热段的散热损失很小，予以忽略。特定工况下:p =5 kPa，测量湿度Y =15 %，最大流速c=200 m/s下，湿度均方根误差计算公式为

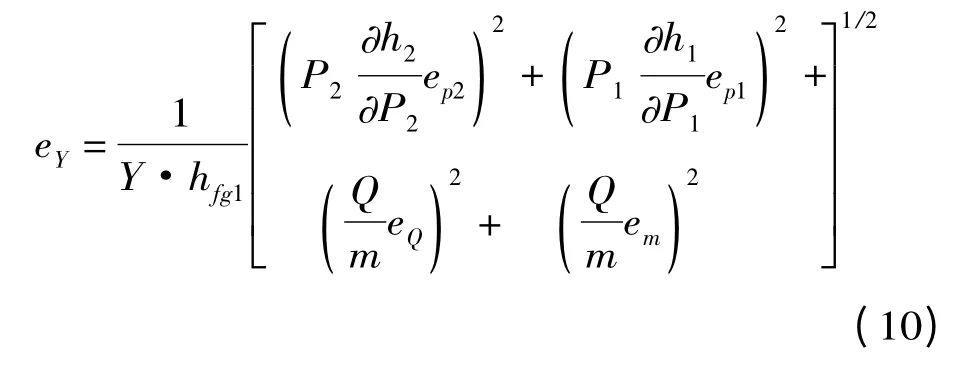
将各个参数代入式(10)，得到湿度的误差eY=0.002 732，则湿度测量的绝对误差ΔY = Y ×eY=0.040 87，则该流动湿蒸汽测量结果的表达式为:Y测=Y真+ΔY=15 % ±0.040 87 %

5 结论

汽轮机末级蒸汽湿度的准确测量，对于汽轮机的经济和安全运行，以及技术改造有重要的意义。

(1)目前湿度测量方法都存在一定的不确定性，影响测量精度的主要因素是热量散失，为了更大程度地提高湿度测量的准确性，减少由于热量散失造成的误差，本文设计了两种基于加热法的汽轮机缸内湿度测量装置。

(2)对于加热法测量蒸汽湿度，不同的湿度测量装置，测量结果精度不同，对于图2 所示的测量装置，计算过程比较复杂，要通过反复的叠加计算，耗时比较多，但是计算结果更加接近实际值。对于图3 所示的测量装置，为保证蒸汽稳定流动，装置前后的压差的数值是用图5 的数值，计算中误差比较大，但其优点在于测量装置简单，容易操作，易于控制。

［1］Bohn D，K Holzenthal．Humidity and turbine drop size distribution measurements in the condensation process ［C］．Proceedings of the 2nd European Conference on Turbomachinery，Antwerpen，Belgium，1997．55-63．

［2］王京，马洪波．云冈热电供热经济运行分析［J］．电力科学与工程，2008，24 (6):13-15．Wang Jing，Ma Hongbo．Analysis of economical heating operation of Yungang thermoelectric plant［J］．Electric Power Science and Engineering，2008，24 (6):13-15．

［3］刘洪伟，李娟，张春发．汽轮机轴封系统经济性分析方法的研究［J］．电力科学与工程，2008，24 (3):38-40．Liu Hongwei，Li Juan，Zhang Chunfa．Thermal economy analysis method of shaft seal system of steam-turbine［J］．Electric Power Science and Engineering，2008，24 (3):38-40．

［4］Dibelius G H，K Mertens，R U Pitt，et al．Strauf Investigation of wet steam flow in the turbine［C］．Proceedings of the Institute of Mechanical Engineers．Conference on Turbomachinery-Efficiency， Prediction and Improvement， Cambridge，U．K．，1987:135-143．

［5］Vomela J．Experimental Study of the turbine stages［C］．Power Machines Conference，WBU in Pilsen，2002．

［6］Bohn D，N Surken，F Kreitmeier．The nuclear phenomena of multi-stage low pressure turbine［C］．Proceedings of the 5th European Conference on Turbomachinery，Prague，2003．

［7］Lampart P．Numerical optimization of the low pressure turbine last stage of three-dimensional cascade under different operating conditions［C］．5th European Conference on Turbomachinery，Prague，2003．

［8］Dykas S．Numerical calculation of the flow of steam condensation［J］．Scientific Bulletin of Academic Computer Centre in Gdansk，2001，5 (4):519-535．

［9］Chmielniak T，Hukowicz．Under different conditions by Cascade Flow survey［C］．ZN Politechniki' SlRaskiej，1995．66-69．

［10］Craig HRM，HJA．Cox．Axial turbine performance is estimated［J］．Journal of the Institute of Mechanical Engineers，1970，71 (32):407-424．

［11］Aleksejeva R N，E A Bojcova．Approximation method to calculate the cascade of energy loss［C］．Teploenergetika，1973．12，21-25．

［12］Gyarmathy G．Grunglagen einer theory on Nassdampfturbine［C］．Dissertation．Juris Verlag，Z¨urich，1960．

［13］AEA Technology．CFX-TASC flow's theory［C］．2001:Version 2，11-20．

［14］Menter F R．Two-equation eddy viscosity turbulence model in engineering applications［J］．AIAA Journal 1994:32，1598-1605．

［15］Menter F R．The eddy viscosity turbulence model［J］．Journal of Fluids Engineering，1996:118，514-519．

［16］Wagner W．The thermodynamic properties of industrial water and steam from IAPWS［J］．Journal of Engineering Gas Turbines and Power 2000:122，150-182．

［17］White A J，J B Young，P T Walters．Experimental verification of stationary steam turbine blade cascade condensing flow theory［J］．Philosophical Transactions of the Royal Society of London，1996:Series A，354-359．