幅相误差对卫星导航抗干扰性能影响
2012-02-15张星,王伶,张昆,杨睿
张 星, 王 伶, 张 昆, 杨 睿
(1.西北工业大学 电子信息学院,陕西 西安 710072;2.北京邮电大学 电子工程学院,北京 100876)
卫星导航系统无论在军事还是在商业中都已显示出巨大的应用价值,但是由于卫星导航信号的本身特性,较小的干扰就可使导航接收机无法正常工作[1]。在理想条件下,自适应天线技术可以有效地抑制干扰而保留期望信号 ,但是在实际系统中常常存在各种幅度和相位误差,如阵元相位误差、阵元位置扰动误差和信号波前畸变[2]。幅相误差将会使抗干扰的性能急剧下降甚至无法有效抑制干扰[3],因此,在抑制干扰信号之前需要对接收信号进行幅相误差校正[4]。
自上世纪80年代中期以来,国内外一些学者已经提出很多有效的幅相误差校正方法[5-6]。由于卫星导航系统一般都为窄带系统,阵列各通道的频率特性比较理想,即幅频响应在带宽内起伏比较小,相频响应近似为一条直线。此时可以认为各个通道之间幅相误差仅仅相差一个复常数,只需在中心频率上校正即可。因此,针对卫星导航系统,一般采用点频福相误差校正,该类方法计算量较小、结构简单,易于实现等优点。
文中首先在理论上分析了幅相误差对卫星导航系统抗干扰后输出信干噪比的影响,接着进行了大量的仿真实验验证了理论分析的正确性,并且得到以下结论:幅相误差校正主要校正阵列接收通道的相位误差对抗干扰性能的影响,而阵列接收通道的幅度误差对抗干扰性能的影响校正效果有限,在射频前端设计时,应尽量保证各通道幅度一致性。
1 理论分析
考虑N元阵列,Γ为通道幅相不一致性系数矩阵,N(t)为通道噪声向量,假设各通道噪声为相互独立的加性高斯白噪声,且与信号及干扰不相关,均值为0,方差为σ2n。对于点频幅相误差校正,阵列接收数据模型为:
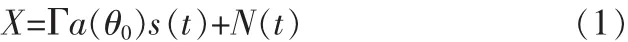
其中,Γ=diag[r1,r2,…,rN],其中 ri=Aiejφi,Ai和 φi分别为第i个通道的幅度误差和相位误差,a(θ0)为点频信号导向矢量。
由于Rx包含了幅相误差的因素,则抗干扰自适应处理权值为:

当不存在干扰时,抗干扰权值可以表达为:
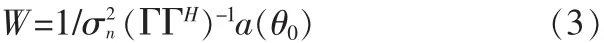
输出信噪比为:
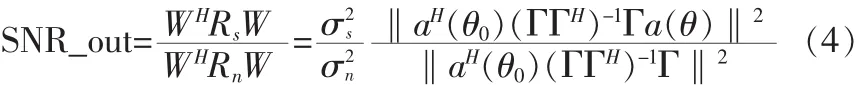
则信噪比损失为:
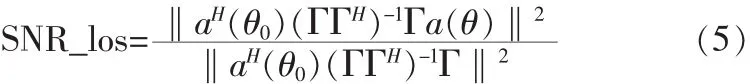
当存在干扰时,由于卫星导航信号很微弱,因此
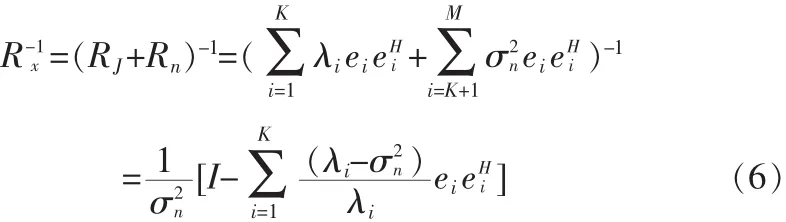
当干噪比较大时,即 λiσ2n:
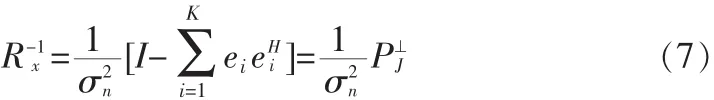
P⊥J为干扰在噪声子空间上的投影。抗干扰权值可以表示为:
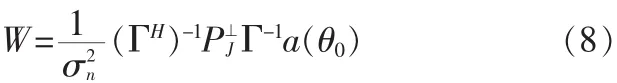
由于Γ为一对角阵,则在干扰位置处的方向增益为:
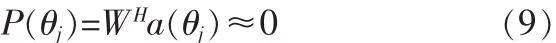
说明可以在干扰位置形成零陷。
抗干扰后输出信干噪比为:
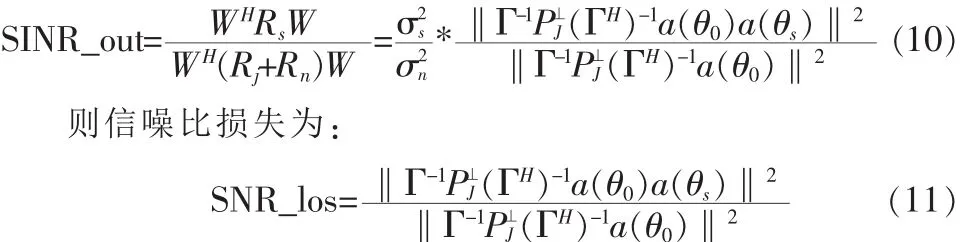
2 仿真实验
2.1 相位校正性能分析
仿真条件:采用七阵元面阵,阵元排布方式如图1所示。卫星输入信干噪比为-60 dB,其中输入信噪比为-20 dB,干扰位置为(120°,45°)。
图1 阵元排列方式Fig.1 Arrangement of the array
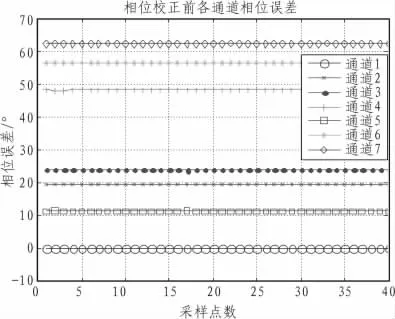
图2 相位校正前各通道相位误差Fig.2 Phase error of each channel before correction
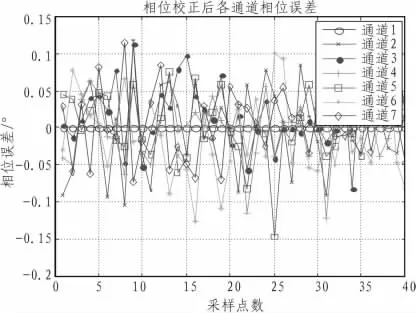
图3 相位校正后各通道相位误差Fig.3 Phase error of each channel after correction
图2 以及图3为相位误差为30°时幅相误差校正前及校正后各通道相位信息,从图中可以看出,校正前各通道与标准通道的相位差较大,而校正后与标准通道的相位差很小,各通道的相位基本保持一致。
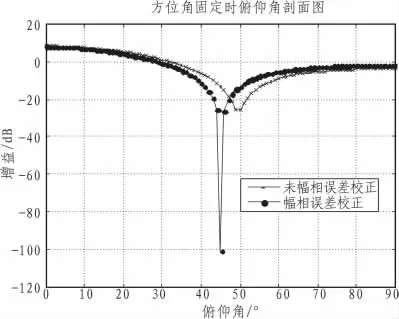
图4 相位校正前后干扰位置俯仰角剖面图Fig.4 Profile of the pitch angle of the interference location before and after phase correction
图4 和图5分别为当相位不一致性为30°时,在零陷位置的剖面图。从图中可以看出,当未进行幅相误差校正时,零陷深度较浅,同时零陷位置发生了较大偏差,而进行幅相误差校正后,零陷位置很精确并且达到较深的零陷深度。
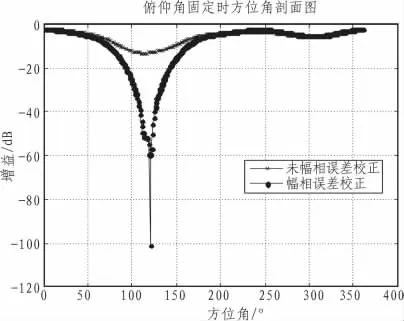
图5 相位校正前后干扰位置方位角剖面图Fig.5 Profile of the azimuth angle of the interference location before and after phase correction
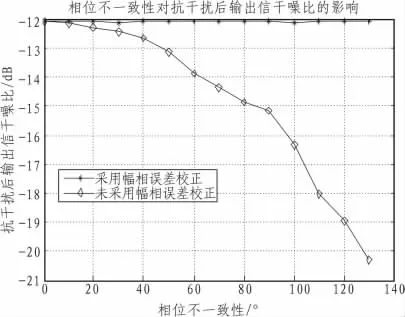
图6 相位不一致性对输出信干噪比影响Fig.6 Affect of the phase inconsistencies on the output SINR
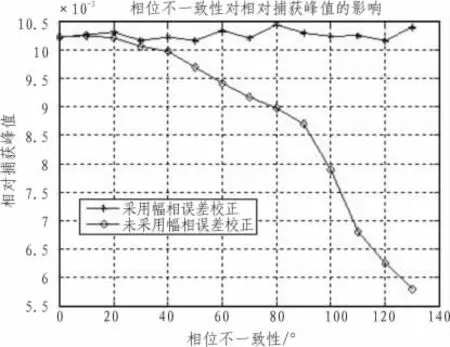
图7 相位不一致性对相对捕获峰值影响Fig.7 Affect of the phase inconsistencies on the relative capture peak
图6 和图7分别表示了相位不一致性对抗干扰后输出信干噪比及相对捕获峰值的影响,从图中可以看出,当未进行相位误差校正时,随着相位不一致性的增加,抗干扰后输出信干噪比及相对捕获峰值急剧下降,而当采用相位误差校正后,抗干扰后输出信干噪比及相对捕获峰值基本保持在一个稳定值,且和无误差时相差无几。
2.2 幅度校正性能分析
仿真条件:采用七阵元面阵,阵元排布方式如图1所示。卫星输入信干噪比为-60 dB,其中输入信噪比为-20 dB,干扰位置为(120°,45°)。
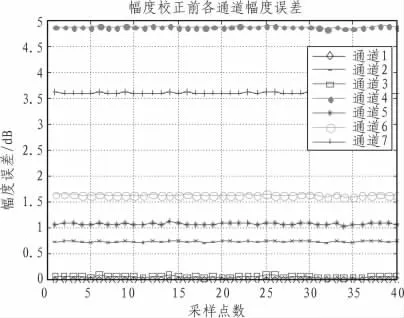
图8 幅度校正前各通道相位误差Fig.8 Amplitude error of each channel before correction
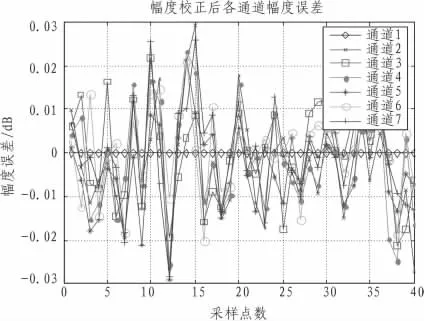
图9 幅度校正后各通道相位误差Fig.9 Amplitude error of each channe after correction
图8 以及图9为幅度误差为2 dB时幅相误差校正前及校正后各通道相位信息,从图中可以看出,校正前各通道与标准通道的相位差较大,而校正后与标准通道的幅度差很小,各通道的幅度基本保持一致。
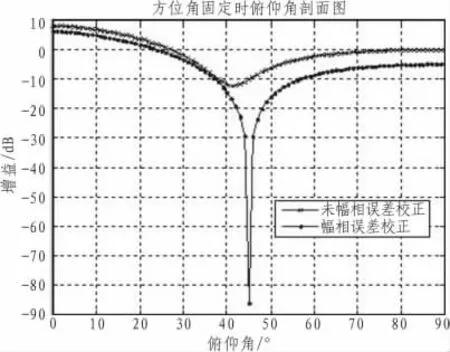
图10 幅度校正前后干扰位置俯仰角剖面图Fig.10 Profile of the pitch angle of the interference location before and after amplitude correction
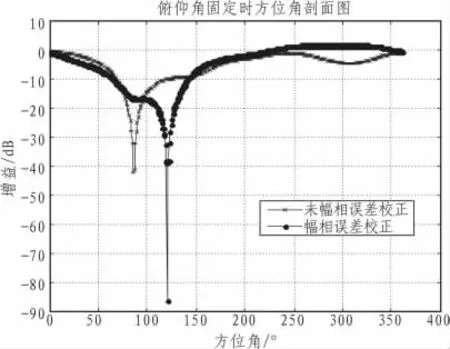
图11 幅度校正前后干扰位置方位角剖面图Fig.11 Profile of the azimuth angle of the interference location before and after amplitude correction
图10 和图11分别为当幅度不一致性为2 dB时,在零陷位置的剖面图。从图中可以看出,当未进行幅相误差校正时,零陷深度较浅,同事零陷位置发生了较大偏差,而进行幅相误差校正后,零陷位置很精确并且到达较深的零陷深度。
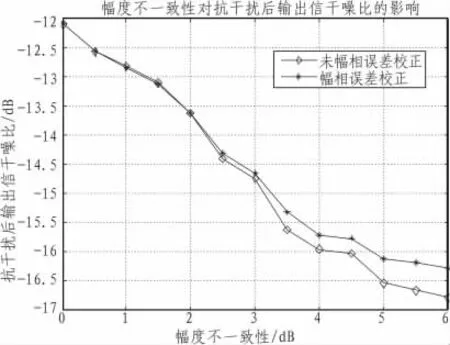
图12 幅度不一致性对输出信干噪比影响Fig.12 Affect of the amplitude inconsistencies on the output SINR
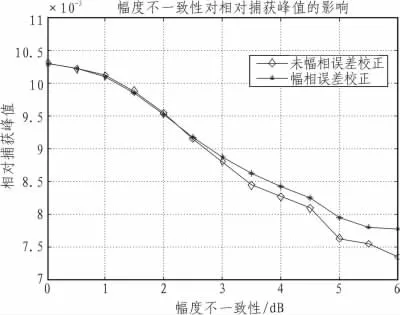
图13 幅度不一致性对相对捕获峰值影响Fig.13 Affectoftheamplitudeinconsistenciesontherelativecapturepeak
图12 和图13分别表示了幅度不一致性对抗干扰后输出信干噪比及相对捕获峰值的影响。从图中可以看出,当不考虑幅度误差校正时,随着幅度不一致性的增加,抗干扰后输出信干噪比及相对捕获峰值急剧下降,而当采用幅度误差校正后,抗干扰后输出信干噪比及相对捕获峰值亦随着幅度误差增加下降剧烈,但是性能要比无幅度误差校正要优一些,这主要是因为幅度误差校正只是提高或者降低了某些通道信号的幅度,而无法改变通道中信号的信噪比,从而幅度误差校正对抗干扰性能的提升能力有限,因此,在射频前端设计时,应尽量保证各通道幅度一致性。
3 结 论
本文主要分析了幅相误差对卫星导航抗干扰系统的影响。首先在理论上分别分析了当不存在干扰和存在干扰时幅相误差对输出信干噪比的影响,然后通过大量实验分别仿真分析了相位及幅度误差对抗干扰后输出信干噪比及相对捕获峰值的影响,从分析的结果得到以下结论:幅相误差校正可以很好的校正相位误差对抗干扰性能的影响,但是幅度误差对抗干扰性能的影响很难通过幅相误差校正解决。相位校正对抗干扰性能的提升效果明显,而幅度校正对抗干扰性能的提升效果有限。例如当相位误差为60°时,输出信干噪比降低2 dB,相位校正后可以提高2 dB;当幅度误差为3 dB时,输出信干噪比降低2.5 dB,但幅度校正仅能提升0.15 dB。因此,在设计射频通道时,应尽量保证各通道的幅度一致性。
[1]贾洪峰,刘尚合.用于GPS接收机的功率倒置阵列抗干扰性能研究[J].军械工程学院学报,2001,13(4):30-33.JIA Hong-feng,LIU Shang-he.Study on the anti-jamming performance of power inverse arrays used in GPSreceiver[J].Journal of Ordnance Engineering College,2001,13(4):30-33.
[2]于斌,尹成友,黄冶.阵列天线互耦、阵元位置误差和通道不一致性的校正[J].微波学报,2008,24(4):56-59.YU Bin,YIN Cheng-you,HUANG Ye.Calibration method for mutual coupling,sensor position uncertainty and channel mismatch[J].Journal of Microwaves,2008,24(4):56-59.
[3]卢艳娥,谈展中,丁子明.通道失配和天线互耦对GPS抗干扰天线的影响 [J].北京航空航天大学学报,2005,31(10):1110-1115.LU Yan-e,TAN Zhan-zhong,DING Zi-ming.Effect of channel mismatch and mutual coupling on GPS adaptive array[J].Journal of Beijing University of Aeronautics and Astronautics,2005,31(10):1110-1115.
[4]王永良,吴仁彪.通道不一致性、互耦对最优阵列处理器的影响[J].系统工程与电子技术,1993(2):49-55.WANG Yong-liang,WU Ren-biao.Effect of channel tochannel mismatch and mutual-coupling on the performance of optimum array processor[J].System Engineering and Electronic Technology,1993(2):49-55.
[5]倪晋麟,苏为民,储晓彬.幅相不一致性对自适应阵列性能的影响[J].应用科学技术,2000,18(3):223-226.NI Jin-lin,SU Wei-min,CHU Xiao-bin.The effect of amplitude and phase errors on the performance of adaptive array antenna[J].Journal of Applied Sciences,2000,18(3):223-226.
[6]张曙光,丁淑娟,孙广俊,等.幅相误差对数字波束形成系统的影响[J].现代电子技术,2008,31(3):7-10.ZHANG Shu-guang,DING Shu-juan,SUN Guang-jun,et al.Effect of amplitude-phase errors on digital beam forming system[J].Modern Electronic Technique,2008,31(3):7-10.
