基于子带分解和比例归一化算法的回声消除器设计与仿真

徐 丽，巨永锋

（1.长安大学 信息工程学院，陕西 西安 710064；2.长安大学 电子与控制工程学院，陕西 西安 710064）

近年来随着VoIP的普及，网络回声消除已经成为当今的研究热点。在网络回声消除器中，通常需要对大量的抽头权系数进行更新，且其输入信号的相关性较强。这些特点使得传统的LMS和NLMS自适应滤波算法在这类应用中受到了限制。由Lee等人 提出的归一化子带自适应滤波器（NSAF）因其固有的去相关和最小扰动特性较好地解决了这些问题[1]。然而在网络回波路径的冲激响应向量中大多数元素较小，只有部分元素较大[2]。因此让那些活跃的系数有更大的更新速度可以加快收敛速度，传统的子带滤波算法由于未利用回声路径的稀疏特性，收敛速度会变得缓慢。文献[3]提出的PNLMS算法具有很快的初始收敛速度，但如果回声路径发生色散，则其收敛速度远低于NLMS算法。针对这个问题，人们提出了各种改进算法，其中文献[4]基于最速下降理论提出了MPNLMS算法，其采用最优的步长控制矩阵使得大系数和小系数同时收敛到最优值的某个领域，从而使算法在整个自适应过程中都保持很快的收敛速度，但其每次迭代增加了对数运算，为此，文献[4]同时提出了SPNLMS算法，其使用一个折线近似估计MPNLMS算法中的函数，在不损失性能的前提下免去了MPNLMS算法中的对数运算。该算法在遇到稀疏回声路径时，收敛速度大大快于NLMS算法；在遇到色散回声路径时，收敛速度不低于NLMS算法。然而当输入序列为有色信号或强相关性的语音信号时，以上比例算法的收敛速度明显下降。针对这一问题，文中结合子带滤波和比例算法的优点，提出了一种基于子带分解结构的分割式比例归一化算法。仿真结果表明，当输入为强相关信号时，新算法具有更快的收敛速度和系统跟踪能力。

1 归一化子带滤波算法

图1是网络回声消除器的原理框图，图中w（n）=[w1（n）w2（n）...wL（n）]T表示自适应滤波器在时刻的系数向量，L 为自x（n）h（n）产生回声y¯（n）， 回声y¯（n）混和近端干扰信号 v（n）得到期望信号d（n）。声回波消除即通过使用FIR自适应滤波器w（n）来模拟冲激响应长度为L的回波路径h（n），产生一个同回声y¯（n）尽量相似的信号 y（n）， 然后将 y（n）从期望信号 d（n）中减去，从而达到回声消除的目的。

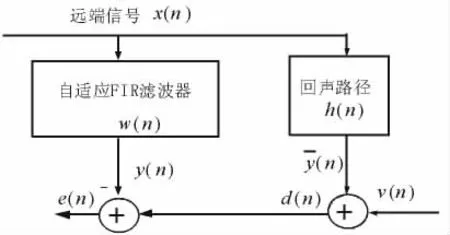
图1 网络回声消除器原理框图Fig.1 Network echo canceller diagram

文献[1]将横向自适应FIR滤波器扩展到子带方法，提出了图2所示的子带自适应滤波器结构。图中↓B和↑B分别表示对信号进行B倍抽取和B倍内插，输入信号矢量x（n）=[x（n）x（n－1）...x（n－L+1）]T经过分析滤波器组 Fi（z）（0≤i＜B－1）分解为B个位于不同频带上子带信号，用xi（n）表示，然后在每个子带上分别进行自适应信号处理，再把处理后的信号通过综合滤波器组Gi（z）合成为全频带信号进行输出。

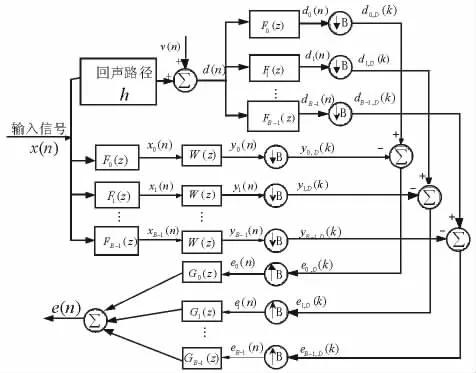
图2 子带自适应滤波器结构Fig.2 Sub-band adaptive filter structure

根据文献[5]，归一化子带滤波算法（Sub-band NLMS）系数更新过程可表示为：

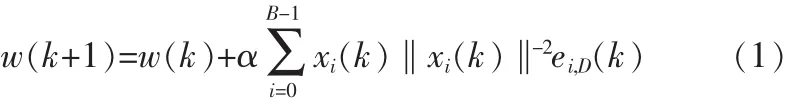
其中 w（k）=[w1（k）w2（k）...wL（k）]T为自适应滤波器在时刻的系数向量，且每输入B个信号样值，该向量更新一次；xi（k）=[xi（kB）xi（kB－1）...xi（kB－L+1）]T为 kB 时刻的第 i个子带输入信号向量；ei，D（k）=di，D（k）－xTi（k）w（k）为 kB 时刻第 i个子带系统误差信号；α为步长。

2 分割式比例归一化子带滤波算法

归一化子带滤波算法算法中系数的更新速度是一样的，而在实际情况中回声路径是稀疏的，有大量系数为零。因此让那些活跃的系数有更大的更新速度可以提高系统的收敛速度。受此启发，文中在Sub-band NLMS算法中引入一个步长控制矩阵G（k）=diag{g1（k） g2（k）...gL（k）}分别为各个滤波器系数赋予不同的步长，步长控制因子gl（k）值大意味着滤波器系数有一个较大的步长。于是可得到Sub-band PNLMS的系数更新表达式：

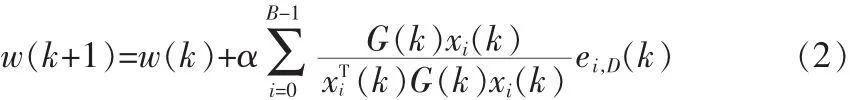
G（k）中步长控制因子gl（k）的递推计算可归纳为:

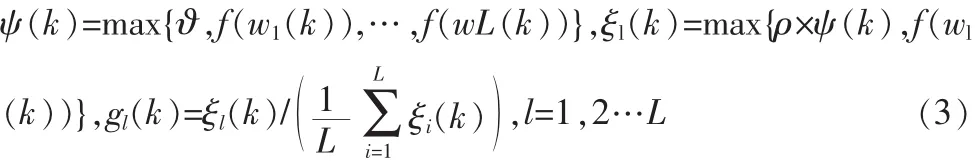
其中：ϑ用来防止所有系数为零时算法冻结，一般取ϑ=0.01； ξl（k）用于对 ψ（k）进行轻微调节；ρ用于防止系数相差过大而引起参数更新停止，取值在 1/L～5/L 之间。 根据 f（wl（k））定义的不同可分为几种不同的Proportionate算法。文献[3]中通过令f（wl（k））=|wl（l）|，使得各个系数的步长与该系数的绝对值成正比，加快了活动系数的收敛速度，其具有很快的初始收敛速度，但后期收敛速度会变得很慢。文献[4]提出的MPNLMS算法利用μ函数替代|wl（k）|解决了这一问题，但其每次迭代中需要L次对数运算，为降低计算复杂度，在保证收敛性能相当的情况下，文献进一步提出使用一个折线来近似μ函数，将其运用到文中所提算法中，可得到 Sub-band SPNLMS 中 f（wl（k））的计算表达式:

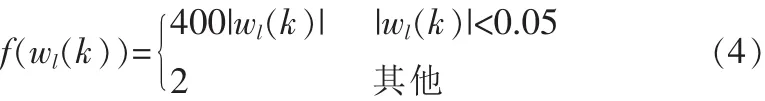
综上所述，Sub-band SPNLMS算法系数更新过程可描述为：

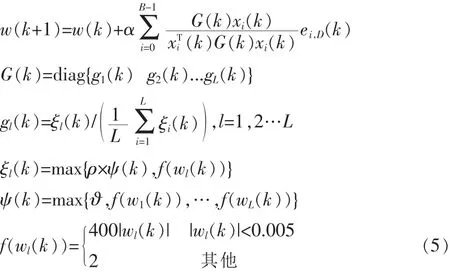
3 仿真分析

为了检验文中算法在回声消除中的性能，利用文献[6]中方法模拟生成一稀疏回声路径（如图3所示，其冲激响应长度L=512），比较文中所提Sub-band SPNLMS算法与文献[1]所提Sub-band NLMS算法、文献[4]所提SPNLMS算法收敛性能。分别使用高斯白噪声通过一阶系统 1/（1－0.8z－1）产生的 AR（1）过程和真实语音作为远端输入信号，期望信号由输入信号通过回声路径再迭加上与输入信号独立的白高斯观测噪声v（n）得到，信噪比为20 dB；Sub-band SPNLMS算法和Sub-band NLMS算法中子带数目B=4。各种算法步长参数设置为：α=0.2。

图3 稀疏回声路径Fig.3 Sparse echo path

图4 输入信号为AR（1）时，3种自适应回声消除算法收敛性能比较Fig.4 Comparison of convergence of three adaptive echo canceller algorithm when input is AR（1）

图4 比较了使用图3所示的稀疏回声路径时新算法和相关自适应算法的收敛性能，该仿真的输入为AR（1）过程，可以看出，Sub-band SPNLMS比SPNLMS有更快的初始收敛速度。在相同的子带数目下，新算法与Sub-band NLMS相比，因其利用了回声路径的稀疏特性，在稳态性能相当的情况下，具有更快的收敛速度。

图5比较了输入为语音时新算法和相关算法的收敛性能，其他仿真条件与图4中相同，从图中可以看出：文中所提的Sub-band SPNLMS算法在这种输入信号的情况下，具有比其他2种算法更快的收敛速度，且比Sub-band NLMS算法稳态性能有约2 dB的提高。

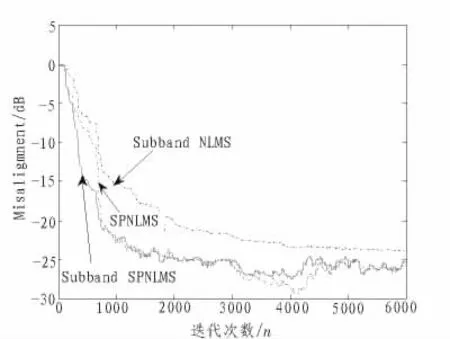
图5 输入为语音信号时，3种自适应回声消除算法收敛性能比较Fig.5 Comparison of convergence of three adaptive echo canceller algorithm when input is speech signal

图6 比较了相关算法跟踪能力，仿真回声路径突变发生在2.5×104迭代时，其变化情况为由图3所示的回声路径向右平移12个样本。其它仿真条件与图4中相同。由图可见当回声路径突然变化后，Sub-band SPNLMS算法与Sub-band NLMS算法相比，有更快的跟踪速度。

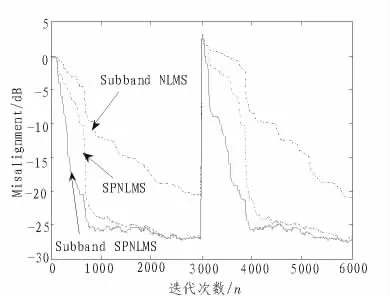
图6 3种自适应回声消除算法跟踪能力比较Fig.6 Comparison of tracking of three adaptive echocanceller algorithm

4 结 论

文中将已有的适用于稀疏信道的Proportionate NLMS算法向子带自适应滤波器进行扩展，提出了一种基于子带分解结构的分割式比例归一化算法。理论分析和仿真结果表明：所提算法能够迅速有效地接近最佳权系数值，并能获得较小的稳态失调；当输入为AR（1）过程和强相关的语音信号时，本文算法均较Sub-band NLMS算法和SPNLMS算法有更好的性能，而且当系统发生突变时，该算法仍能快速收敛。

[1]Lee K A，Gan W S.Improving convergence of the NLMS algorithm using constrained subband updates[J].IEEE Signal Processing Letters，2004，11（9）:736-739.

[2]Godavarti M，Hero III AO.Partial update LMSalgorithms[J].IEEE Signal Processing， 2005，53（7）:2382–2399.

[3]Duttweiler D L.Proportionate normalized least-mean-squares adaptation in echo cancellers[J].IEEE Trans.Speech Audio Process，2000，8（5）：508–518.

[4]Hongyang D，Doroslovacki K.Improving convergence of the PNLMS algorithm for sparse impulse response identification[J].IEEE Signal Processing Letters，2005，12（3）:181-184.

[5]Nekuii M，Atarodi M.A fast converging algorithm for network echo cancellation[J].IEEE Signal Processing Letters，2004，11（4）:427-430.

[6]Andy WH，Khong，Naylor PA.Efficient useof sparseadaptive filters signals[J].System and Computers，2006，10（6）：1375-1379.