机械激励下的板件声学包装中频段插入损失研究

卢兆刚，郝志勇，郑 旭，杨 骥

(浙江大学 能源工程学系，杭州 310027)

汽车、飞机以及船舶的板件声学包装对产品的内部噪声控制起着至关重要的作用，现代设计方法需要在概念设计阶段对产品的声学性能进行了解和掌握，就需要对其声学性能进行准确而迅速地预测。板件声学性能主要由吸收系数和声传递损失(Sound transmission loss)等参数进行评价。对于板件声学包装性能的研究多集中在空气传播声的传递损失研究。但当传播路径上机械传播声为主要控制对象时，对这种情况下的声学包装性能的研究则鲜见报道。

对机械传播声下的声学包装性能可以使用插入损失来进行评估［1］。获取声学包装插入损失的方法主要有测试手段和预测方法。测试手段可以根据已有的测试标准进行测试，而预测的常用方法有统计能量分析(SEA，Statistical Energy Analysis)方法、有限元方法(FEM Finite Element Method)和传递矩阵法(TMM，Transfer Matrix Method)。

SEA方法在高频段具有较高的精度，但由于需要较高的模态密度来作为统计样本，不适用于中低频段。Robert与Graik［2］利用修正的SEA方法对复合板质量控制区的声传递损失进行了预测和分析，并与试验结果进行了分析和对比，发现该修正的SEA方法预测复合板件在质量控制区的传递损失性能相符。Liu和Tao［3］利用SEA方法对汽车仪表板的声传递损失进行了预测和仿真，并与试验结果进行对比，在中高频段定性趋势与试验结果符合较好，但是在模态控制区的传递损失与试验结果相比误差较大。

FEM方法在低频段应用广泛，预测精确，尤其是对于各种复杂的结构、不同边界条件及载荷下的传递损失更加有效。但是由于在模态密集的中高频段需要较为致密的单元，且声学包装的单元处理较为复杂，导致计算成本过高，并没有得到广泛的应用。Lee与Ng［4］研究了加筋板在密闭声学空间内的声学插入损失，对板件部分采用有限元模型，而对于声学空间部分则采用文献［5］中提到的解决方案，研究了边界条件、加强筋、声学空间模态以及结构模态对插入损失的影响。其分析频段主要局限于板件的模态控制区，对于模态密集处的声插入损失预测会出现较大误差。Hong与Raveendra［6］和陈馨蕊、郝志勇［7］利用有限元方法对汽车前围板的声学传递损失进行了预测和分析。在他们的研究中，半球形的声场部分采用了有限单元进行建模，在模态控制区其预测结果与试验结果比较相符，但是对于模态密集的中高频处，其预测精度同样会下降。同时，该方法对于仪表板的声学包装的处理存在相当的困难，为后续的声学包装设计带来困难。

TMM方法对受到声学激励的传递损失的预测较为准确，得到了广泛的应用。但对于机械激励下的传递损失计算很少见诸于文献。Attala［8］利用TMM方法对在声学及机械激励下加筋板传递损失进行了预测，并与传统的FEM方法、Wave－based方法进行了对比，同时也与试验结果进行了分析对比，得出该方法的计算速度比传统的FEM方法要迅速，预测结果也是可以接受的。但这种方法对施加在其上的声学包装的计算及设计面临着困难。

本文利用混合FE－SEA方法建立了板件声学包装中频段插入损失预测模型，计算速度快，计算精度与试验符合较好，对声学包装等参数的处理也比较方便。利用该模型改变声学包装的设计要素，并对不同要素变化时的插入损失进行了预测，得出具有一般意义的结论。

本文分为三个部分:首先建立插入损失的理论模型、试验模型、混合FE－SEA预测模型和计算及数据后处理流程;其次，利用混合FE－SEA模型对两种特殊的声学包装进行了预测，并与试验结果进行比较;最后，基于建立的混合FE－SEA模型对各设计要素的变化时，对声学包装在机械激励下的插入损失变化规律进行了研究，得出了一般性的结论，为机械激励下的声学包装设计提供了指导性的建议。

1 插入损失模型

1.1 理论模型

声学包装的插入损失定义为施加了声学包装板件的传递损失减去无任何声学包装的板件的传递损失［8］。如式(1)所示:其中的∏是指输入功率或辐射功率，输入功率式(2)定义:

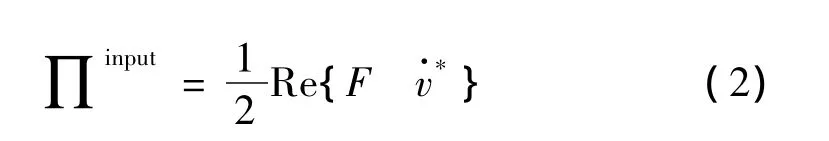
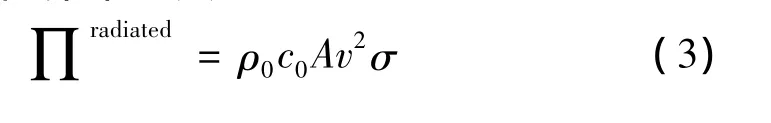
辐射功率由式(3)定义:其中:ρ0为流体密度，c0为声波在流体中的传播速度，A为模型辐射面积，v2为模型响应速度的均方根值，σ为模型的辐射效率。ρ0c0为流体的特性阻抗。

1.2 试验模型

根据1990年修订的SAE J 400汽车材料及总成的隔音性能试验室测量标准，测试装置由一块1 mm厚钢板(0.9×0.6 m2)及分别施加其上的两种典型声学包装和激振器组成。钢板镶嵌在混响室和半消声室中间的隔墙上，在激励点布置一个加速度传感器和力传感器，以得到激励点的输入功率。辐射声功率由声强探头测得，声强探头置于半消声室内。为防止激振器产生辐射声场而影响测试精度，采用一定的封装隔声措施密封，试验场地和测试结果由项目合作伙伴提供。

1.3 混合FE-SEA模型

在商业软件VA One中建立混合FE-SEA模型。对板件部分采用FEM建模，简支边界条件，分析带宽为100～630 Hz，每个波长下至少划分6个网格，生成1 275个四边形壳单元。外部直达声场采用软件中的SIF(Semi infinite fluid，半无限大流体)模块建立，SIF与有限元子结构外部的FE Faces建立连接，表示该有限元子系统向SIF辐射声能。激励力在与试验激励相同部位施加单位力激励。激励力幅值与试验中的并不相同，原因是插入损失理论上与激励力的幅值并无关系。

测试和仿真对象为两种典型的声学包:轻质的泡沫层覆盖声学包(Foam-backed)和重质的质量层声学包装(Septum-backed，图3)。夹心层、泡沫覆盖层以及质量层的材料参数如表1所示。为了方便起见，本文余下部分分别用FB和SB来代表泡沫层覆盖声学包和质量层覆盖声学包。建模时，在声学包装和基板板件之间需要添加1 mm的空气层，以防止预测结果出现较大的误差［9］。

1.4 计算流程和数据处理

1.4.1 FE 子系统和 FE Face

在VA One中首先建立平板SEA系统，利用自带网格剖分工具对SEA系统进行剖分并建立平板的FE子系统，同时删除原SEA子系统，在生成FE子系统的同时会在FE的表面生成FE Face子系统。在VA One中，FE Face的作用是与其他相邻子系统进行连接，如SEA子系统、BEM子系统及FE声学空腔子系统，同时也是各种均布声学激励和声学包装的施加部位。

1.4.2 激励和消声室

在FE子系统上，与验证试验中激励力施加的相同部位处施加点力激励。消声室采用SIF来进行模拟，FE子系统与SIF建立连接，表示该子系统向此半无限大声场辐射能量，并且无反射，流场介质默认为空气，SIF的入射声功率就是透射侧的声功率。

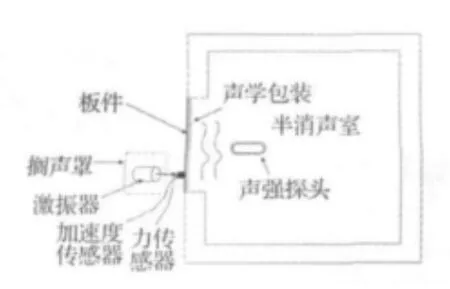
图1 试验组成Fig.1 Test setup

图2 混合FE-SEA模型Fig.2 Hybrid FE-SEA model

1.4.3 计算有限元模态特性及参数

对有限元子系统的边界处所有节点进行3个平动自由度的约束，建立简支边界条件。在板件的透射侧的FE Face上分别施加FB和SB声学包后，利用有限元自带的计算程序得到该约束板件的模态参数，包括模态振型矩阵、模态频率、质量矩阵、刚度矩阵、模态密度等。

1.4.4 最终计算

在得到有限元板件系统的模态信息后，提交最终计算，得到了施加了声学包装后的板件输入功率和SIF的入射功率等参数。

图3 声学包装结构Fig.3 Structure of the sound-package

表1 纤维夹心层、泡沫层以及质量层参数特性Tab.1 Characteristic of fibrous，foam and septum

1.4.5 数据后处理

首先利用软件计算到光板的FE子系统的输入功率和SIF的入射功率，然后再计算施加了两种声学包装的输入功率和入射功率，利用式(1)进行计算，得到了各频段下的两种声学包装的插入损失。

2 混合FE-SEA计算结果与试验结果的对比

汽车的中低频计算与仿真一直是业界的难题之一［10］。车用板件中低频带分布在 0 ～500 Hz［10］。0 ～100 Hz的低频段使用FEM方法可以比较准确的计算，本文主要分析在100～630 Hz的中频带，1/3倍频程。两种声学包装的测试结果和混合FE-SEA方法预测结果对比如下:

图4 FB与SB插入损失的计算结果与测试结果对比Fig.4 Comparison of IL between predicted and the test results

从图中可以发现，在机械激励下，两种声学包装的中频段插入损失，模型预测结果和测试结果在趋势上较为相符。误差基本在3 dB以内，是工程可以接受的误差范围，FB声学包的预测精度比SB的预测精度要差，并且FB声学包误差在500 Hz以后有增大的趋势。在仿真模型中，声学包装的插入损失低谷在315 Hz，而测试的结果在分别在200 Hz和250 Hz。原因可能是安装误差使测试的模型边界条件并不是准确的简支边界条件，造成了测试和仿真构件动态特性的差别。

FB声学包与SB声学包的插入损失在100～315 Hz频段上有明显差别，后者比前者要高;在200 Hz时SB的插入损失达到最大值，而FB则基本上在125～160处有着最大的插入损失。两者的插入损失低谷也不同，对于FB而言，插入损失的低谷值依然为正值，而SB在250～315 Hz频段上的插入损失为负值。究其原因，SB声学包的外层质量覆盖层－夹心层－基板板件组成了双层隔声结构，第一个隔声低谷出现在“双层板共振频率”处，频率一般在 300 ～500 Hz［10］，当夹心层由空气变成柔性介质时，频率点还要降低15%。而FB的声学包都是细声性能较好的轻质材料，不符合双层隔声结构的特征。

上述结果表明，利用混合 FE－SEA模型预测声学包装在中频段的插入损失的精度是满足工程要求的。利用该模型，对声学包装的夹心层厚度、夹心层流阻率、背后空气层厚度及板件材料属性等参数对插入损失的影响进行研究，得出有意义的结论，为声学包装的优化设计提供有指导性的意见。

3 参数改变对插入损失的影响

3.1 夹心层厚度的影响

为了研究夹心层厚度对两种声学包装插入损失的影响，将夹心层的厚度从5～30 mm范围内改变，改变步长为5 mm，计算结果如图5所示:

图5 厚度变化时的插入损失计算结果Fig.5 IL results from variant core thickness

由图5(a)可以看出，夹心层厚度对FB声学包的插入损失在100～250 Hz频带上有显著影响。随着厚度的增加，插入损失随之增加，当由5 mm至10 mm时，增加幅度最大，但随着厚度的继续增加，带来的益处也在减小。考虑到成本的限制，10～15 mm的夹心层厚度比较合适。

由图5(b)可以看出，夹心层厚度对SB声学包的插入损失在100～400 Hz频带上有显著影响，且变化规律较为复杂。当从5 mm变化至20 mm时，100～200 Hz频段的插入损失还是随着厚度的增加而增加的，但当厚度变为25～30 mm时，插入损失在125 Hz处迅速下降。且随着厚度的增加，声学包装的隔声峰值频率点也有后移的趋势。从图上还可以看出，夹心层厚度对声学包装的插入损失低谷却没有影响，但是低谷处插入损失的幅值却随着厚度的增加而下降。

不同的夹心层厚度带给两种声学包装不同的插入损失变化规律，这主要还是由于两种声学包装覆盖层的不同所造成。由于所关注的是机械激励下的插入损失，决定这种插入损失的是包括了基板板件和声学包装在内的结构整体模态特性。夹心层厚度的变化使整体厚度发生改变。对于FB声学包，由于泡沫材料是轻质材料，声学包对系统的模态特性影响较小，夹心层厚度变化不会对整体模态特性带来显著影响，只是增加夹心层的总声流阻，所以插入损失的变化只是幅值的改变，而不牵涉到峰谷值频率特性的改变。SB声学包就截然不同，由于覆盖层对声学包装而言是均匀质量层，面密度达到4 kg·m－2，对板件系统的模态特性有着关键性的影响。当夹心层厚度变化时，系统的整体厚度发生改变，不仅夹心层的总流阻发生改变，模态特性也发生了变化。同时，SB声学包的质量覆盖层与板件及夹心层组成了双层隔声结构，夹心层厚度的变化造成了构件“双层板共振”频率的改变，所以此时插入损失的改变不仅仅是幅值的变化，还牵涉到隔声低谷和峰值频率点的移动。

通过上述分析可以发现，夹心层厚度变化可以具有轻质覆盖层的FB声学包的插入损失带来影响，但只是在100～250 Hz的频段内带来幅值上的变化，且变化量在1～3 dB之间，插入损失的峰谷值频率特性却变化不大。而对于面密度较大质量覆盖层的SB声学包装而言，夹心层厚度的变化对插入损失的影响不仅仅是数值上的改变，峰谷值频率特性也得到了很大的改变。究其原因，对机械激励下对声学包装插入损失峰谷值频率特性影响最大的，是包括基板板件和声学包装在内的构件整体模态特性，哪个参数对整体模态特性影响最大，插入损失的峰谷值频率特性对哪个参数就最敏感。

3.2 夹心层流阻率的影响

为了验证上述结论，再改变一个对整体模态特性影响不大的参数:夹心层流阻率。令其从10 000～60 000(N·s·m－4)之间变化，步长为10 000，研究两种声学包插入损失的变化规律。计算结果如图6所示:

图6表明，当夹心层的流阻率由10 000～60 000(N·s·m－4)变化时，两种声学包装的插入损失只是在幅值发生变化，峰谷值频率特性却不会发生改变。

虽然幅值上会发生改变，但SB声学包的插入损失所受到的影响要小于FB声学包，其原因依然在于夹心层的外部覆盖层。有研究表明，当声学包装的流阻为空气特性阻抗的 2～4倍，即流阻在800～1 600(N·s·m－3)时，该声学包装有着最好的吸声效果［1］。因为夹心层的流阻率为33 000(N·s·m－4)，厚度为12.5 mm，所以其流阻为 412.5(N·s·m－3)，泡沫覆盖层的流阻为 87 000 ×0.005=435(N·s·m－3)，所以FB声学包的总流阻为847.5(N·s·m－3)，理论上有较好的吸声效果，而SB声学包的覆盖层为质量层，流阻率可以认为无限大，夹心层流阻率的变化与其插入损失关系不大。

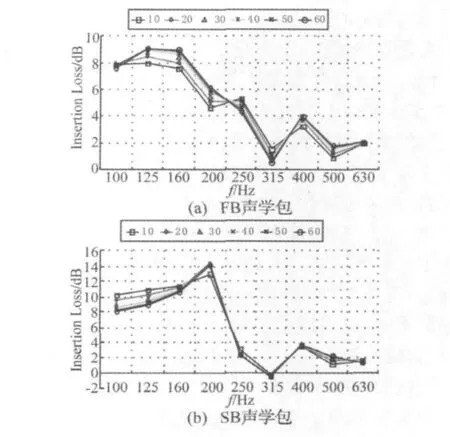
图6 流阻率变化时的插入损失计算结果Fig.6 IL results from variant core flow-resistivity

3.3 声学包装背后空气层厚度的影响

图7 空气层厚度变化时的插入损失计算结果Fig.7 IL results from variant air-gaps thickness

有峰值大小的改变。对于SB，在160～315 Hz的频带内插入损失的幅值和峰谷值频率特性改变都很大。尤其是在200 Hz处，当空气层厚度为1 mm和2 mm时为插入损失的极大值点。与FB不同的改变趋势的原因，与夹心层厚度变化带来的影响是一样的:空气层厚度的变化造成了构件的模态特性的变化。但需要注意的是，并不是空气层厚度越大插入损失的效果越好，在空气层厚度为5 mm时，FB与SB声学包的插入损失全面下降。因此，设置空气层厚度为1～2 mm最佳。

通过上述分析，发现声学包装与基板板件之间的附着安装条件可以通过设置一定厚度的空气层来近似代替，厚度设置为1～2 mm最佳。

3.4 基板板件材料的影响

原基板板件为钢板，将其换作高阻尼复合板材(MPS)，研究板件材料属性的变化对声学包装插入损失影响的规律。复合板件的总厚度与原板件相同，都为1 mm，由两块薄钢板及位于其中的粘弹性薄板组成。其各层属性如表2所示，计算结果如图8所示。

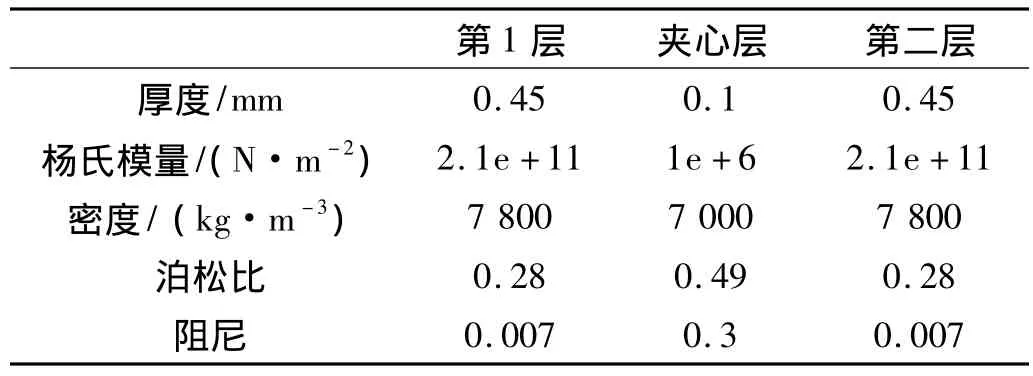
表2 MPS各层材料属性Tab.2 characteristic of the MPS panel

图8表明，当构件的基板是具有高损耗因子的复合阻尼板时，FB声学包在机械激励下的插入损失可以

下面考虑夹心层背后空气层厚度的影响。汽车的声学处理中，声学包装中的夹心层一般和板件有一定的空气层间隔，如顶棚的声学包装［10］。目的是为了形成空气声腔，和两侧结构组成双层隔声结构，有效阻隔外部空气声的传递。在本文的验证试验中，夹心层与板件之间不是直接黏结，而是附着其上，由于夹心层材质较软，刚度较小，和板件贴附并不紧密，在对声学包装建模时需要考虑这种安装条件。为了分析这种附着安装条件下设置空气层与否和设置的厚度为多少，将空气层厚度由0～5 mm范围内变化，步长为1 mm，计算结果如图7所示:

图7表明，建模时如果不考虑空气层的影响，预测的插入损失误差将会非常大。对FB声学包的影响有100～160 Hz，315～630 Hz频带;对 SB声学包的影响主要集中在200～630 Hz的频带内。分析其原因，如果不考虑空气层，软件将会把夹心层和基板板件直接耦合，直接耦合表示夹心层与基板紧密黏合，这与实际安装情况并不相符。在软件中，夹心层和板件的的直接耦合与通过空气层与基板板件进行耦合下的刚度特性是截然不同的。因此在夹心层与基板之间设置一定的空气层厚度是必要的，厚度的大小通过以下分析得到。

图8 板件材料属性变化时的插入损失计算结果Fig.8 IL results from the MPS panel

当空气层厚度由1～5 mm变化时，对于FB，在100～315 Hz的频带内，插入损失随着空气层厚度的增加而减小，峰谷值频率特性没有发生改变，这主要是空气层厚度的变化带来空气层的阻尼总量的改变，造成只忽略不计。而SB声学包在100～250 Hz的频带内却依然具有较好的插入损失。其原因是两种构件的模态特性由不同的子部件决定所造成。对于FB，整体模态特性主要由基板板件贡献;对于SB，质量层和基板板件同时对整体模态特性有着关键的影响。

值得注意的是，虽然FB在复合阻尼板中的插入损失较小，并不代表此种情况下就应该使用SB声学包装。相反，在中低频段，基板板材本身的模态特性由于高阻尼的影响而受到较大的抑制，机械激励下的结构声传播不会成为主要传播路径。声学包装只需要考虑高频段的空气声传播，在高频下，FB相较于SB具有较好的声吸收性能，所以复合阻尼板的声学包装还是应以FB为主。

4 结论

本文建立了一种简单、迅速和有效的模型对机械激励下声学包装的中频插入损失进行预测和分析，模型的正确性得到了试验测试的验证。基于此模型，对两种典型的声学包装的设计要素进行了改变，预测了夹心层厚度、夹心层流阻率、声学包装背后空气层的变化给插入损失计算带来的影响，还考虑了基板板材的阻尼特性变化时，对声学包装的插入损失的影响。得出一个具有指导意义的结论:在机械激励下的结构声传播为主要传播路径时，整体构件的模态特性决定了声学包装的插入损失的峰谷值频率特性。在声学包装的设计要素里，哪些参数对包括基板板件在内的整体模态特性影响最大，插入损失的峰谷值频率特性对哪个参数就最敏感。所以当机械激励下结构声传播的声学包装的插入损失需要改变峰谷值频率特性而适应声学治理的需要时，应该设计合理的夹心层厚度和质量覆盖层的面密度，从而改变整体构建的模态特性，使声学包装能够有针对性地对某些频段下结构声传播进行有效地抑制。

［1］ 马大猷.噪声与振动控制工程手册［M］.北京:机械工业出版社，2002，405.

［2］ Craik R J M.Non－resonant sound transmission through double walls using statistical energy analysis［J］.Applied Acoustics，2003，64:325－341.

［3］ Liu W L，Tao D.Use of statistical energy analysis method to predict sound trasnmission loss of sound barrier assemblies［C］.SAE，1999－01－1707.

［4］ Lee Y Y，Ng C F.Sound insertion Loss of stiffened enclosure plates using the finite element method and the classical approach［J］.Journal of Sound and Vibration，1998，217(2)，239－260.

［5］ Lee Y Y.Structural-acoustic analysis of close－fitting enclosures［D］.Hong Kong:The Hong Kong Polytechnic University，1995.

［6］ Hong K L，Raveendra S T.Sound transmission loss analysis of an automotive dash by finite element method［C］.SAE，2003－01－1613.

［7］ 陈馨蕊，郝志勇，结构－声耦合法在汽车仪表板隔声性能仿真分析中的应用［J］.振动与冲击，2009，28(8):154－157.

［8］ Rhazi D， Atalla N. Transfermatrix modeling ofthe vibroacoustic response of multi－materials structures under mechanical excitation［J］.Journal of Sound and Vibration，2010，329:2532－2546.

［9］ VA One Foam，VA One，2007.

［10］ 庞 剑，谌 刚，何 华.汽车噪声与振动－理论与应用［M］.北京:北京理工大学出版社，2006，85.