基于捷联导引头最优制导律工程实现研究❋
2012-02-09林德福杜运理
徐 平,王 伟,林德福,王 江,杜运理
(1.北京理工大学宇航学院,北京 100081;2.中国兵器科学研究院,北京 100081)
随着现代国防科技的飞速发展,对武器装备的要求越来越高,为了使武器装备达到未来战争的要求,近年许多学者对最优制导律进行了深入研究,并取得了许多成果.这些最优制导律基本可以分为以下3类:①考虑导弹过载限制和目标机动的最优制导律[1-2];②考虑自动驾驶仪动力学的最优制导律[3-5];③增加末端约束的最优制导律[6-8].本文推导了一种考虑自动驾驶仪动力学和目标机动的最优制导律,并分析了基于捷联导引头这种最优制导律的实现方案.捷联导引头相对于框架式导引头主要拥有以下优势[9]:①质量和体积优势,由于去掉了框架,使得导引头的质量和体积大大地减小,节约了宝贵的弹上空间;②最大跟踪弹目视线角速度不受机械限制,可以跟踪高机动目标;③对导弹的过载不敏感;④相对于框架式导引头而言成本低廉;⑤可靠性高.正是捷联导引头拥有以上的明显优势,所以捷联导引头技术受到了各国军方的高度重视.研究基于捷联导引头的最优制导律实现拥有非常重大的现实意义.
1 最优制导律推导
在推导最优制导律前,先做以下几个假设:①导弹自动驾驶仪可以用一个二阶欠阻尼环节表示;②在制导过程中目标以常值过载做机动;③忽略除导弹自动驾驶仪以外所有环节的动力学.图1给出了基于以上假设的简化制导系统原理框图.其中aT表示目标过载,aL表示弹体过载,˙aL表示弹体过载对时间的一阶导数,¨aL表示弹体过载对时间的二阶导数,aC表示过载指令,y表示导弹位置误差,˙y表示导弹速度误差,¨y导弹过载误差,Tm表示自动驾驶仪的时间常数,μm表示自动驾驶仪的阻尼系数.
根据图1可得

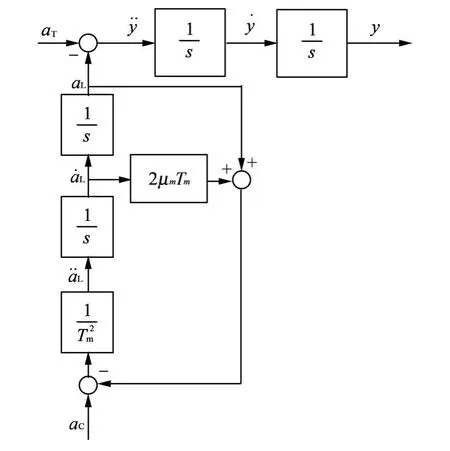
图1 简化制导系统原理框图F ig.1 Simplified guidancesystem p rinciple block diagram


最优制导律是一种使导弹以最小的控制能量准确命中目标的控制策略,根据以上结果运用最优制导律的这一原则可得最优制导律如(1)式所示,其中˙q表示弹目旋转角速度,v表示弹目接近速度.

2 基于捷联导引头最优制导系统模型的建立
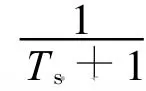

图2 基于捷联导引头最优制导系统框图Fig.2 Optimal guidance system based on strapdown seeker block diagram
由图2可得系统状态方程为

系统量测方程为


3 仿真分析
3.1 卡尔曼滤波器公式
由式(2)表示的系统的卡尔曼滤波公式如下[13]:
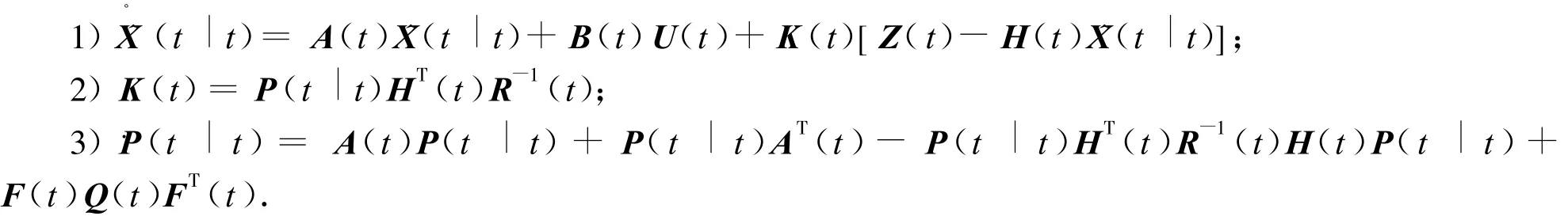
3.2 仿真算例
设制导初始时刻存在瞄准误差角 ε,目标以加速度a T做机动.取T=0.02 s,N=3,v=220m/s,μm=0.1,Tm=0.08 s,k s=1.0,k g=1.0,a T=10m/s,ε=10°.取系统干扰噪声的功率谱密度矩阵


图3给出了卡尔曼滤波器输出的弹目视线角速率估计值和实际弹目视线角速率值的对比曲线,由图3可以知,卡尔曼滤波器可以快速准确地估计弹目视线角速率.图4给出了卡尔曼滤波器输出的目标机动过载与目标实际机动过载的对比曲线,由图4可以看出,卡尔曼滤波器最后可以准确地估计出目标过载,但是需要一个较长的过渡时间.

图3 弹目视线角速率估计值与实际值对比曲线Fig.3 Curve of line of sight rate estimation value com pare w ith the actual value

图4 目标过载估计值与实际值对比曲线Fig.4 Curve of target acceleration estim ation value compare with the actual value
图5给出了使用最优制导律和比例导引弹体的实际过载曲线对比,由图5可以看出,采用最优制导律弹体最大过载小于比例导引的最大过载,而且采用最优制导律在制导末端弹体过载远小于采用比例导引制导律的情况.图6给出了采用最优制导律和采用比例导引的弹体位置误差对比曲线,由图6可以看出,采用最优制导律的弹体位置误差远小于采用比例导引时的情况.

图5 弹体过载对比曲线Fig.5 Missile acceleration com parison curve

图6 位置误差对比曲线Fig.6 Position error comparison curve
4 结束语
本文推导了考虑目标机动和自动驾驶仪动力学的最优制导律,并运用卡尔曼滤波技术估计最优制导律过载指令形成需要的状态,给出了一种基于捷联导引头的最优制导律实现方案.仿真结果表明,虽然卡尔曼滤波器估计目标过载的时候,过渡过程较长,但是采用了最优制导律的导弹无论是在过载方面还是位置误差方面都要远优于采用比例导引的导弹.
[1] Hexner G,Pila A W.A p ractical stochastic optimalguidance law for a bounded acceleration m issle[J].A IAA,2010(8):54.
[2] 谢希权,易华.主动雷达型空空导弹最优末制导律工程研究[J].系统工程与电子技术,2000,22(12):66-68.
Xie Xiquan,YiHua.Study on optimal terminal guidance law for AAM[J].Systems Engineering and Electronics,2000,22(12):66-68.(in Chinese)
[3] 刘德忠,刘洁慧,朱晓东.二次型一阶最优制导律的一种实现方案[J].航空兵器,2007(6):3-5.
Liu Dezhong,Liu Jiehui,Zhu Xiaodong.Implementation of a sing le-lag optimal control guidance law[J].Aero Weaponry,2007(6):3-5.(in Chinese)
[4] 庄志洪,路建伟,丁庆海,等.一种基于二阶制导系统的最优导引律研究[J].南京理工大学学报,1999,23(3):237-239.
Zhang Zhihong,Lu Jianwei,Ding Qinghai,etal.Performance analysis of oneop timal guidance law for2-orders system[J].Journal of Nanjing University of Science and Technology,1999,23(3):237-239.(in Chinese)
[5] Jalali-NainiSH.Modern explicit guidance law for high-order dynam ics[J].JGuidance,2004,27(5):918-922.
[6] Vitaly Shaferman,Tal Shima.Linear quadratic guidance laws for imposing a term inal intercept ang le[J].Journal of Guidance,Control,and Dynam ics,2008,31(5):1400-1412.
[7] 孙未蒙,郑志强.多约束条件下对地攻击的最优制导律[J].兵工学报,2008,29(5):567-571.
Sun Weimeng,Zheng Zhiqiang.Op timal guidance law w ith mu ltip le constraints in ground strike[J].A cta Arm a Men Trail,2008,29(5):567-571.(in Chinese)
[8] 刘丹,祁载康.限制导弹落角和落点的最优制导律[J].北京理工大学学报,2001,21(3):278-281.
Liu Dan,Qi Zaikang.Impactangle and final position constrained optimal guidance law[J].Journal of Beijing Institute of Technology,2001,21(3):278-281.(in Chinese)
[9] Captain Thomas,Callen R.Guidance Law Design For TacticalW eaponsW ith StrapDown Seekers[J].A IAA,1979,1732:161-180.
[10] Paul L Vergez.Linear Op timal Guidance for an AIM-9L Missile[J].JGuidance and Control,1981,4(6):662-663.
[11] Gordon K F Lee.Estimation of the Time-to-Go Parameter for Air-to-Air Missile[J].JGuidance,1985,8(2):262-266.
[12] Chang-Kyung Ryoo,Min-jea Tahk,Hangju Cho.Practical Time-to-Go Estimation Methods for Optimal Guidance[J].AIAA,1999,4143:29-37.
[13] G rewalM S,Andrew s A P.Kalman Filtering Theory and Practice[Z].Prentice Hall:Englewood Cliffs,New Jersey,1993.
