基于强度折减法的输电杆塔临坡基础边坡稳定性影响因素分析

何运祥，徐力，聂卫平

(广东省电力设计研究院，广州市 510663)

0 引言

目前，对边坡上输电杆塔的稳定性研究多基于平坦地势的结果，或者集中考虑杆塔结构的变化响应，对结构下部的土体和边坡的稳定性研究较少［1-2］，如风荷载作用下塔基的边坡，特别是高边坡的稳定影响分析并不多见［3］。随着我国电力建设的发展，输电线路走廊越来越紧缺，线路路径区域的地形越来越复杂，山区输电线路的杆塔基础将不可避免地位于山顶或半山腰等陡峭地势［4-6］，因此，研究输电线路塔位边坡的稳定性有着重要的工程价值［7-8］。500 kV胪岗—祯州送电线路工程B09号原状土杆塔基础外缘离坡肩距离较近，该边坡在自身稳定的基础上还要承担较大的杆塔荷载，边坡稳定存在着相当的风险［9-10］。本文针对该杆塔临坡基础边坡，采用强度折减法对其边坡的稳定性进行计算，分析了坡角、坡顶距、基础埋深对边坡稳定的影响。

1 强度折减法

1.1 强度折减法原理

将岩体工程材料的粘聚力c、内摩擦角φ同时除以折减系数Ft，得到一组新的粘聚力c'、内摩擦角φ'，将其作为新的力学参数代入有限元方程试算，当边坡符合给定的临界破坏的判定条件时，所对应的折减系数Ft被称为边坡的最小稳定系数Fs，即强度折减安全系数。计算中，假设弹性模量、泊松比为不随c、φ变化的定值［11-13］。

1.2 边坡失稳判据

边坡发生破坏失稳，则会产生较大位移，滑动体由静定状态变为静不定状态，边坡上特征点的位移呈现无限增大趋势。其塑性应变也表现为无限增长的趋势，同时，塑性应变区自坡脚贯通至坡顶［12］。总之，采用有限元强度折减法分析边坡稳定性的关键问题是如何根据计算结果来判别边坡是否处于稳定状态。目前，常用的边坡失稳判据主要有:迭代求解的不收敛性、广义剪应变贯通、塑性区贯通、边坡内某点的位移与折减系数的关系曲线等［13-14］。采用这些方法来确定安全系数具有其各自的特点和实用性。本文根据静力平衡计算是否收敛、特征点的水平位移是否有无限增长的趋势以及剪应变增量是否贯通来评判边坡的总体稳定性［12］。

2 工程概况及其三维有限元模型

2.1 工程概况

500kV胪岗—祯州送电线路为同塔双回线路，全长约186.35 km，途经地形基本为山地、丘陵，仅零星杆塔位于平地、水田。线路荷载大，抗倾覆要求高，所在山区、丘陵地带勘测深度内未见地下水，塔基第4系覆盖层以坡积、残积土为主，一般厚度为2～6 m，部分塔基在8 m勘探深度内仍未见中等风化程度基岩，塔基础采用桩基础。山地丘陵塔基采用天然地基，大部分塔基8 m勘探深度未见地下水。由于斜坡地形的影响，位于斜坡边界条件下的塔基础上拔承载力要比平地低，而斜坡地形对临坡基础承载力的影响规律更为复杂，所以计算时主要考虑杆塔的上拔力和水平荷载，考虑的荷载为:上拔力1.9×106N，水平荷载3.625× 105N。桩基础施工示意图如图1所示，图中:L为坡顶距;D为桩基底板宽度;H为埋深;β为坡角。

图1 B09号桩基础Fig.1B09 pile foundation

2.2 三维有限元模型

建立直角坐标下的边坡三维有限元模型，模型范围:x为－2～4 m，y为0～30 m，z为0～15 m。根据斜坡坡角的不同，划分为2 592～3 616个单元，3 285～4 509个节点，采用位移边界，边坡和桩基均采用实体单元模拟，塔基采用pile单元模拟，桩顶施加外荷载。

根据勘测设计参数，斜坡土层为砂质粘性土，其中土体重度为18.5 kN/m3，弹性模量为10.0 MPa，泊松比为0.25，粘聚力为22.0 kPa，内摩擦角为20.0°，初始地应力只考虑重力，计算采用Mohr-Coulomb本构模型。桩基材料为C25混凝土和II级钢筋，桩基弹性模量为28.0 GPa，泊松比为0.167，极惯性矩为0.377 15 m4，y轴的二次矩为0.188 57 m4，z轴的二次矩为0.188 57 m4，剪切耦合弹簧单位长度的刚度为130.0 GPa，剪切耦合弹簧单位长度的粘聚力为10.0 GPa，剪切耦合弹簧的摩擦角为0.0°，法向耦合弹簧单位长度的刚度为1.3 GPa，法向耦合弹簧单位长度上的粘聚力为10 kPa，法向耦合弹簧的摩擦角为0°。

3 边坡稳定性计算结果分析

3.1 坡角对边坡稳定的影响

分别计算了β为22.5°、33.75°、45°、56.25°、67.5°时，边坡在有桩基础和无桩基础下的强度折减安全系数，结果如图2所示。计算过程中L=1.5 m，D=1.7 m，H=6.0 m。

图2 边坡安全系数随坡角的变化曲线Fig.2Curves of slope's safety factor with slope angle

由图2可知:Fs随着β的增大逐渐降低，且β＜33.75°时，Fs降低速度缓慢，当β＞33.75°时，Fs降低速度明显;β相同情况下，无桩基础边坡安全系数较有桩基础要小，说明该工程中杆塔基础对边坡的保护作用大于其破坏作用，有利于边坡的稳定性。

3.2 坡顶距对边坡稳定的影响

采用强度折减法，分别计算了L为0.75、1.125、1.5、1.875、2、2.25、2.5、3、3.75、5、7.5 m时边坡安全系数，结果如图3所示。计算过程中D=1.7 m，H= 6.0 m。

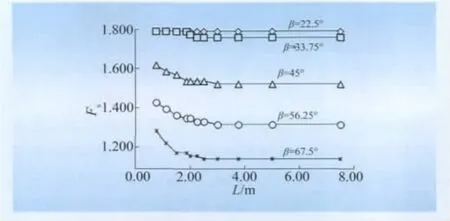
图3 边坡安全系数随坡顶距的变化曲线Fig.3Curves of slope's safety factor with top distance

由图3可知:Fs随着L的增大逐渐降低，最后趋于某个稳定值，且随着β的增大，达到该稳定值的L也在逐渐增大。例如:β=22.5°时，Fs趋于某个稳定值的L为0 m;β=33.75°时，Fs趋于某个稳定值的L为2.25 m;β＞45°时，Fs趋于某个稳定值的L为3 m;β＜33.75°时，Fs随L变化极小，特别是当β=22.5°时，Fs无变化，说明此时L的变化对边坡稳定性没有影响。

3.3 基础埋深对边坡稳定的影响

采用强度折减法，分别计算了H为3、4.5、6、7.5、9 m时的强度折减安全系数，结果如图4所示。计算时L=1.5 m，D=1.7 m，β=45°。

由图4可知:当6 m＜H＜7.5 m时，Fs随H的增大发生突变;H＜6 m或H＞7.5 m时，Fs几乎不变。从该坡度情况下边坡滑移面(图5)可知，6 m＜H＜7.5 m的位置为边坡可能滑移面最下部的位置，因此，当基础穿越滑移面时，容易对边坡稳定性产生破坏。

3.4 参数敏感性分析

确定强度折减法计算的边坡最小稳定系数Fs为考核指标，β、L、H等参数为敏感性影响参数。各影响参数的变化范围为基准值的0.5～1.5倍。

通过计算可以得到β、L、H对边坡最小稳定系数Fs影响的敏感性，Fs随β、L、H变化的曲线见图6。直观分析曲线可知，随着3个影响参数的增大，Fs均有所降低;其中，Fs受β影响最明显，其次为L，最后为H，和常规敏感性分析结果一致。

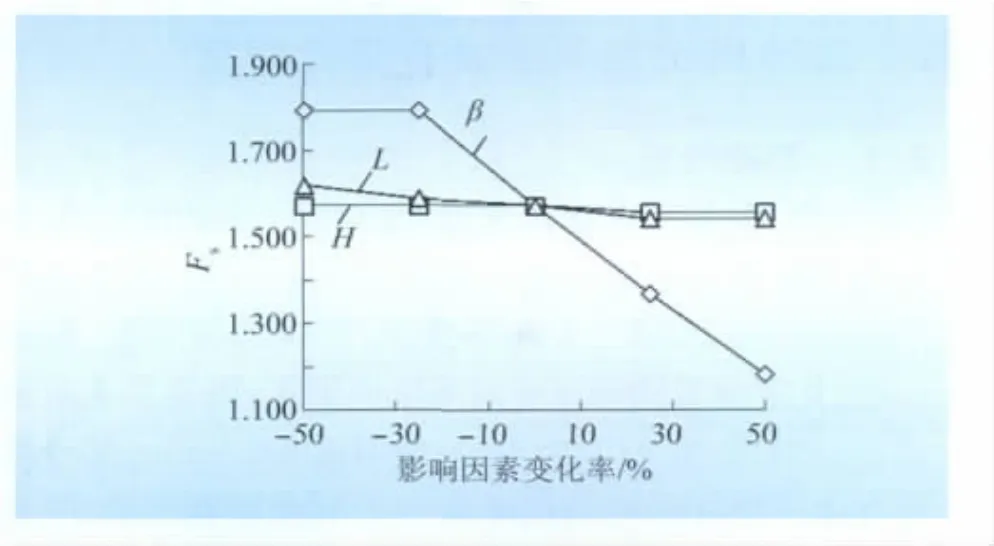
图6 边坡安全系数随影响参数的变化曲线Fig.6Curves of slope's safety factor with influence parameters

根据灰关联敏感性分析原理［13，15-19］，得到比较矩阵和参考矩阵

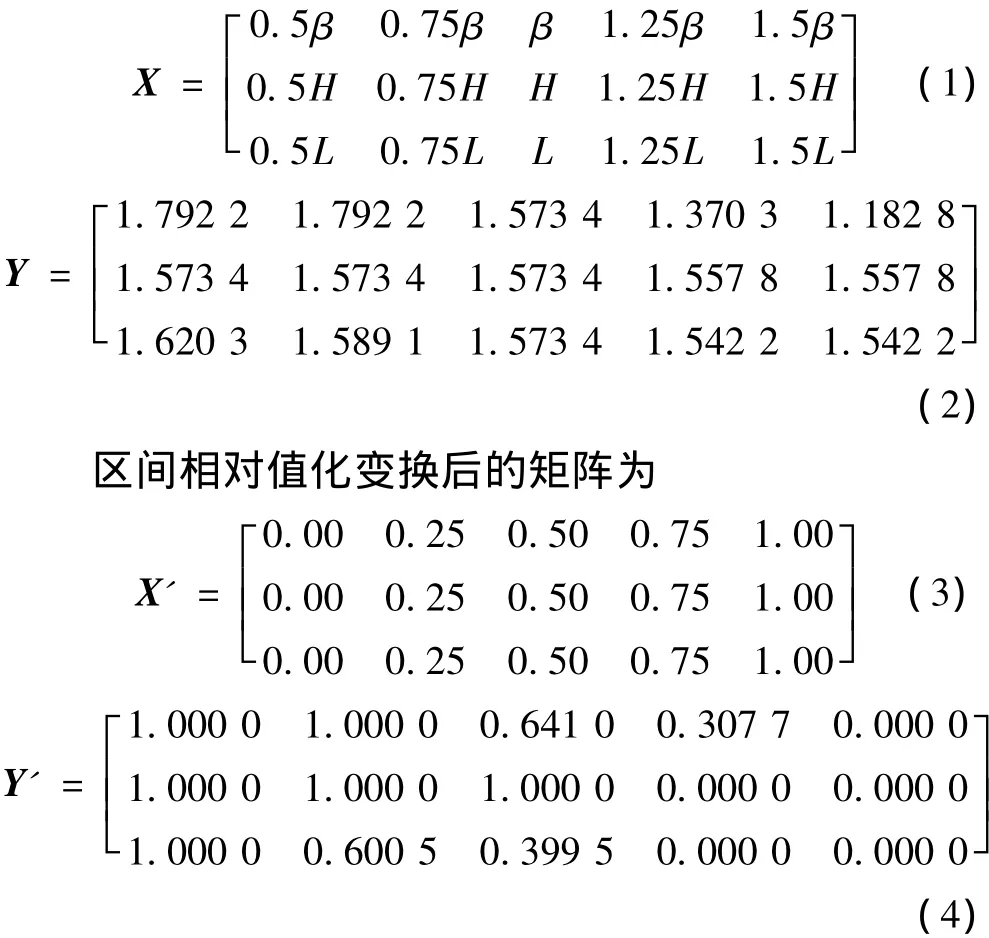
相对值化矩阵通过无量纲化，计算得到塔基边坡的安全系数灰关联系数矩阵γ，进一步取其均值得到边坡强度折减安全系数的关联度序列A

从关联度序列可知，对Fs影响程度由大到小的为L、β、H，表明设计杆塔临坡基础边坡时，为达到边坡的稳定性的要求，应优先考虑优化基础坡顶距，其次为基础坡角，最后在基础满足自身稳定要求的情况下考虑基础埋深。

4 结论

(1)边坡安全系数随着坡角的增大逐渐降低;相同坡角情况下，无桩基础边坡安全系数较有桩基础要小。

(2)边坡安全系数随着坡顶距的增大逐渐降低，最后趋于某个稳定值，且随着坡角的增大，达到该稳定值的坡顶距也在逐渐增大;当基础穿越滑移面时，容易对边坡稳定性产生破坏影响。

(3)采用常规敏感性分析得出，对塔基边坡强度折减安全系数影响程度由大到小的影响因素为坡角、坡顶距、基础埋深，与直观分析结果一致。由于各参数之间量纲的不一致性，常规敏感性分析各参数值的数量级相差很大，计算得到的敏感度往往不具备直接的可比性。为克服该局限性，本文采用灰关联分析方法进行分析，结果表明，对塔基边坡强度折减安全系数影响程度由大到小的影响因素为坡顶距、坡角、基础埋深。

［1］Cai Y X，Could P L，Desai C S.Nonlinear analysis of 3D seismic interaction ofsoil-pile-structuresystemsandapplication［J］.Engineering structure，2002(22):191-199.

［2］范存新，薛松涛，陈铭，等.考虑风－结构－土耦合作用时高层建筑顺风向风振响应分析［J］.力学季刊，2004，25(2):271-278.

［3］金莹，明锋，祝文化.风荷载对输电线塔－高边坡体系的动力影响［J］.武汉理工大学学报，2010，32(12):45-48.

［4］中国电力工程顾问集团公司.提高特高压输电线路可靠性深化研究之新型基础型式专题研究报告［R］.北京:中国电力工程顾问集团公司，2010.

［5］程永锋，邵晓军，朱全军.我国输电线路基础工程现状及存在的问题［J］.电力建设，2002，23(3):32-34.

［6］曾二贤，舒爱强，廖文炜.基于FLAC/Slope模拟分析输电线路塔位边坡的开挖稳定性［J］.电网与清洁能源，2011，27(4):14-18.

［7］曾二贤，陈治.山区输电线路塔位边坡治理方法及技术经济分析［J］.能源技术经济，2010，22(10):20-25.

［8］夏元友，李梅.边坡稳定性评价方法研究及发展趋势［J］.岩石力学与工程学报，2002，21(7):1087-1091.

［9］鲁先龙，程永锋，乾增珍.输电线路斜坡地形原状土基础抗拔计算理论研究［J］.电力建设，2009，30(2):11-13.

［10］林忠民.某山地变电站边坡稳定分析［J］.电力勘测设计，2008 (4):14-17.

［11］赵尚毅，郑颖人，时卫民，等.用有限元强度折减法求边坡稳定安全系数［J］.岩土工程学报，2002，24(3):333-336.

［12］刘立鹏，陈奇，张彬.基于FLAC强度折减理论的边坡稳定性研究［J］.岩土工程技术，2008，22(1):6-10.

［13］刘立鹏，于红杰，陈奇.力学、几何参数对土质边坡稳定的敏感性分析［J］.岩土工程技术，2008，22(3):123-126.

［14］张培文，陈祖煜.糯扎渡大坝设计边坡稳定的有限元分析［J］.中国水利水电科学研究院学报，2003，1(3):207-210.

［15］Turányi T.Applicationsofsensitivityanalysistocombustion chemistry［J］.Reliability Engineering and System Safety，1997，57 (1):41-48.

［16］陈志波，简文彬.边坡稳定性影响因素敏感性灰色关联分析［J］.防灾减灾工程学报，2006，26(4):473-474.

［17］聂卫平，徐卫亚，周先齐.基于三维弹塑性有限元的洞室稳定性参数敏感性灰关联分析［J］.岩石力学与工程学报，2009，28 (S2):3885-3893.

［18］宋雅坤，郑颖人，刘一通，等.土工格栅加筋土挡墙稳定性影响因素敏感性分析［J］.后勤工程学院学报，2010，26(3):1-7.

［19］唐晓松，郑颖人，叶海林.涉水岸坡稳定性影响参数的敏感性分析［J］.后勤工程学院学报，2010，26(3):22-26.

(编辑:蒋毅恒)