±800 kV直流输电线路硬跳线的三维可视化设计
2012-02-08张瑞永吴锁平贾振宏赵新宇张瑞龙
张瑞永,吴锁平,贾振宏,赵新宇,张瑞龙
(江苏省电力设计院,南京市 211102)
0 引言
耐张塔跳线是高压输电线路的重要构件,随着电压等级的提高和导线分裂数的增加,耐张塔上的跳线装置日趋大型化、复杂化[1-2],其合理的设计也成为输电线路设计的重要组成部分。
在±800 kV特高压直流线路中,一般采用双V串硬跳线的形式并适当配重[3-4],以减少跳线风偏和弧垂,压缩杆塔结构尺寸,达到减小耐张塔尺寸、降低工程造价的目的。由于跳线计算过程比较繁琐,目前在工程设计中一般采用电子表格和二维数值计算[5-7]的方法,但效率低、误差大,存在较大的盲目性。
鉴于跳线设计灵活多变的特点,针对±800 kV特高压线路的重要性,本文提出了双V串硬跳线基于CAD交互式的三维解决方案,并用实例验证了该方案的可行性。
1 双V串硬跳线的数学模型
1.1 耐张串偏角的计算
受风速、耐张串质量以及线路上导线质量的影响,耐张串会在相对于来线空间的方向产生水平方向的风偏角及垂直方向的下倾角,进而影响耐张串跳线引流点的位置,因此在跳线计算中应予以重视。
耐张串的风偏角ε和下倾角ξ的计算式分别为
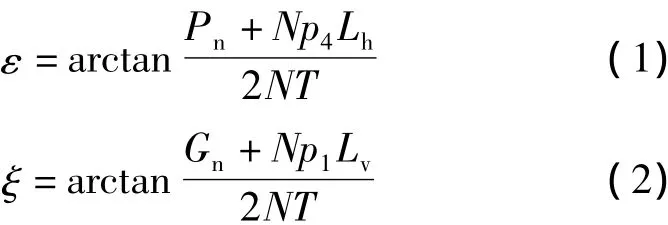
式中:Pn为耐张串的水平风荷载;Gn为耐张串的垂直荷载;N为导线分裂根数;p1为导线的单位长度垂直荷载;p4为导线的单位长度水平风荷载;Lh为计算档导线的水平档距;Lv为计算档导线的垂直档距;T为相应工况的导线张力。
1.2 跳线的状态方程
当风吹过软体跳线时,为了保证不对硬跳线刚体部分产生上拔拉力,需要使软体跳线在刚体出口处留有0.3~0.5 m的弧垂,由此可以计算出软体跳线的最大弧垂为
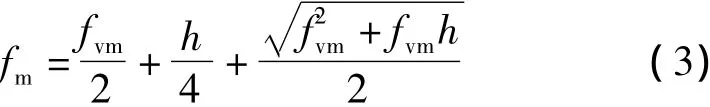
式中:fm为软体跳线的最大弧垂;fvm为软体跳线的最低点相对刚体铝管或鼠笼的垂直距离;h为耐张串引流点与刚体铝管或鼠笼的高差。
结合最大弧垂的斜抛物线公式[8],由fm表示的耐张塔前侧或后侧软体跳线张力为


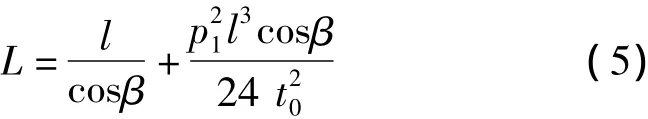
根据跳线线长守恒的规律,计算出各风速条件下的跳线张力t为
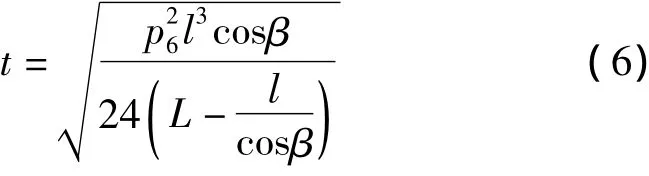
式中:p6为软体跳线的单位长度综合荷载。由纵向张力差产生的跳线串在沿线路方向的偏角为
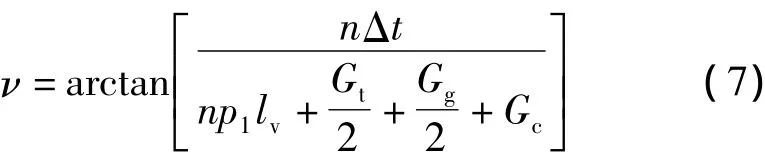
式中:n为跳线分裂根数;Δt为单根软体跳线产生的沿线路方向的张力差;lv为软体跳线靠近刚体侧的垂直档距为单联跳线串质量;Gg为刚体跳线的总垂直荷载;Gc为单联串上重锤的垂直荷载。
利用式(6)~(7)经若干次迭代计算跳线张力和跳线串顺线路偏角,直至精度满足设计要求。
1.3 硬跳线的摇摆角计算
根据以上计算结果,双V串硬跳线的风偏摇摆趋势可表示为
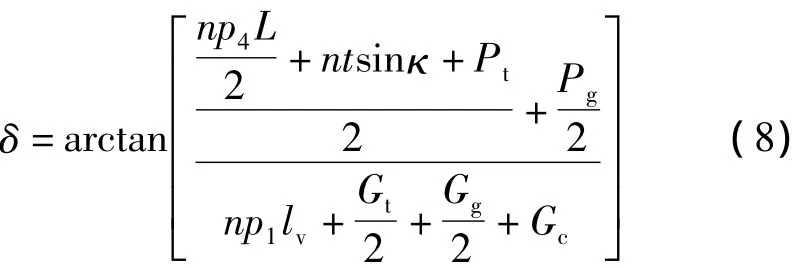
式中:t为计算工况的软体跳线张力;κ为跳线与垂直横担垂线间的夹角;Pt为单串风压;Pg为刚体跳线的总风荷载。
2 跳线电气距离计算方法
2.1 软体跳线的三维轨迹
定义刚体跳线连接处为坐标原点,耐张串引流点为端点,若设l为软体跳线档距,并假设软体跳线在耐张串引流点处的坐标分别为X、Y、Z,则沿跳线两端挂点连线走向的任意点和连线上的辅助档距Δl的坐标关系为
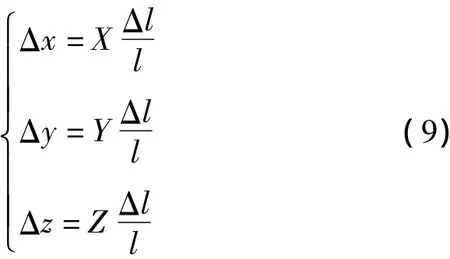
在该连线上的任意点(Δx,Δy,Δz)处,软体跳线的综合弧垂为
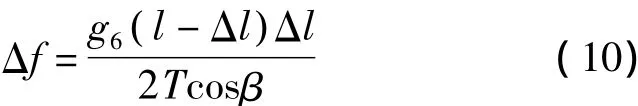
由此可以计算得软体跳线上任意点相对坐标原点的坐标为
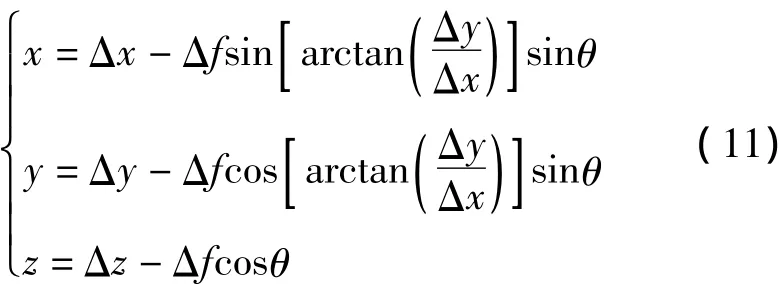
2.2 三维空间坐标变换
三维空间坐标变换是三维跳线计算的关键技术之一,根据三维空间坐标变换技术,可以将复杂的空间计算转换到相对简单的坐标系中处理,从而简化计算过程。
根据坐标转换的物理过程,可得数学模型[10]为
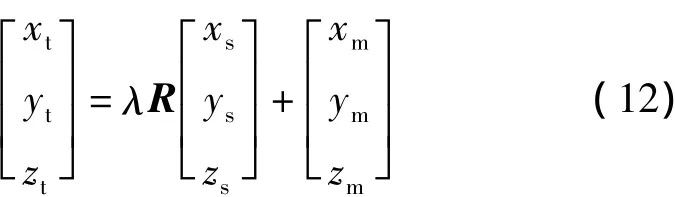
式中:[xt,yt,zt]T为目标坐标;[xs,ys,zs]T为源坐标; [xm,ym,zm]T为平移因子;λ为尺度因子;R为坐标转换旋转矩阵,R=R3R2R1,有
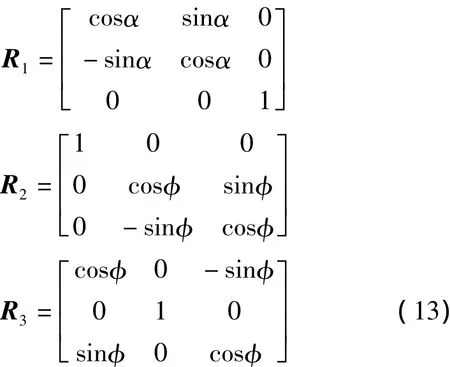
式中:R1为绕Z轴旋转α角的旋转矩阵;R2为绕X轴旋转φ角的旋转矩阵;R3为绕Y轴旋转φ角的旋转矩阵。
2.3 跳线距铁塔的电气距离校验
将跳线带电体部分离散为若干空间点,杆塔的杆件简化为直线段,跳线距铁塔的电气距离计算便简化为点到空间的直线段距离,具体计算为
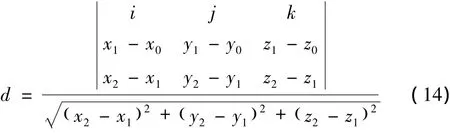
由于最近点有可能位于直线段的两端点以外,因此需判断最近距离点的位置,如果落于两端以外,则判断端点处为最近点。
3 设计实例
根据双V串硬跳线的数学模型和三维空间功能,可以采用可视化设计语言开发具有三维CAD交互功能的双V串硬跳线计算软件。
在±800 kV耐张塔双V串硬跳线设计中,以转角范围为0°~20°、内外侧横担长分别为10、11.2 m的1型耐张塔为例,导线采用6×JL/G1A-900/40,基本风速为33 m/s,操作过电压风速为19.5 m/s,带电作业风速为10 m/s,三联耐张串长为19.2 m,耐张串下倾角和风偏角分别为1°和0°,V型跳线串夹角为90°,跳线串单肢长度为12.9 m,硬跳线及配重为2 t,V型跳线串两挂点分别悬挂于塔身和跳线横担外端,同时考虑V串绝缘子均压环的电气间隙。当fvm=0.5 m时,该塔跳线的设计结果见表1,软件自动生成20°转角的跳线三维CAD模型如图1所示。

±800 kV线路空气间隙及有关尺寸取值:工作电压处为2.3 m,操作过电压处为5.7 m,带电作业处为6.9 m,而人体活动范围(0.5 m)和塔身间隙裕度(0.3 m)需要额外考虑。利用三维可视化软件计算的电气校验结果分别见表2~3。
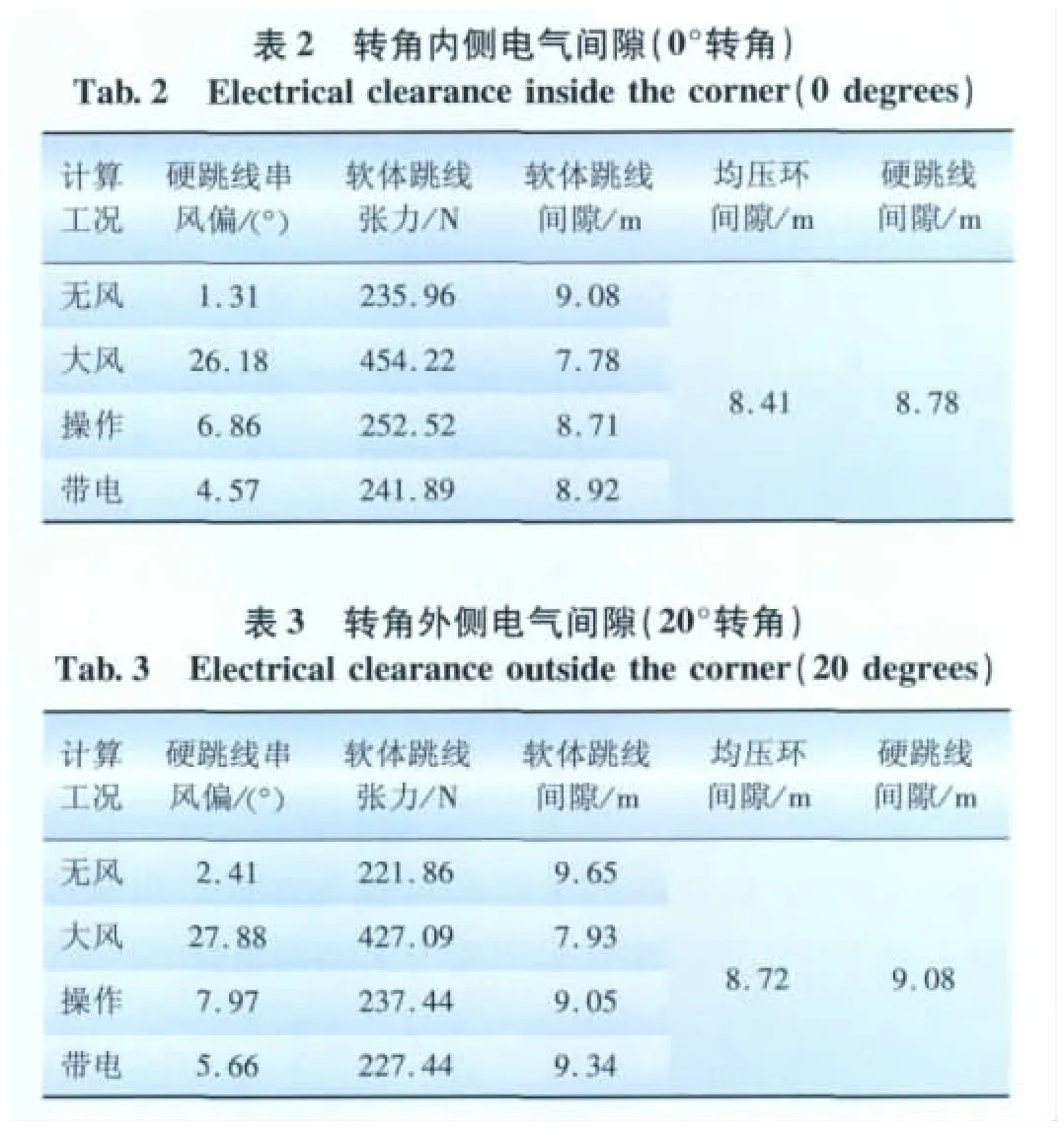
由以上设计结果可以看出,均压环的实际电气间隙要小于硬跳线,而大风电气间隙最小;以三维CAD交互式方法实现的硬跳线设计,不仅可以计算每根软体跳线的线长,还可以验算硬跳线串的风偏角、构件与杆塔的电气距离,空间上的所有尺寸均可以在三维CAD模型图中量测,计算制图结果直观、可靠。
4 结语
本文基于双V串硬跳线的数学模型和三维空间技术,提出了双V串笼式硬跳线的三维解决方案。该方案通过采用可视化设计语言开发三维CAD交互式硬跳线计算软件,其适用范围不受回路数、导线分裂数、塔型结构的限制,重锤个数、预置弧垂均可人为定义;模型编辑、挂点选择定义均可与AutoCAD交互式进行,利用CAD作为三维仓库,可查询每根跳线线长、校验空气间隙方便。
[1]胡选,张要强,潘少成,等.1 000 kV交流特高压有关联双柱组合耐张塔软跳线设计[J].电力建设,2009,30(11):13-16.
[2]吴庆华,李健,万志方,等.500 kV单回路耐张塔边相跳线直跳上绕布置[J].电力建设,2009,30(12):14-17.
[3]孙玉堂,高平.预制式铝管跳线装置的研制与应用[J].电力设备,2005,5(11):53-56.
[4]陈建忠,李勇伟,张小力.750 kV输电线路耐张塔刚性跳线的研究开发[J].电力建设,2006,27(10):19-22.
[5]黄成云.500 kV输电线路耐张塔4-4跳线长度计算[J].电力建设,1997,8(4):26-32.
[6]邹广平,孙刚,任方.考虑弯曲刚度影响的跳线长度计算[J].哈尔滨工程大学学报,2005,13(4):482-486.
[7]尹迪迪,王兴.输电线路跳线弧垂及电气间隙简易计算[J].红水河,2010,29(2):53-56.
[8]邵天晓.架空送电线路的电线力学计算[M].2版.北京:中国电力出版社,2003:81-92.
[9]张殿生.电力工程高压送电线路设计手册[M].2版.北京:中国电力出版社,2003:179-181.
[10]姚吉利.三维坐标转换参数直接计算的严密公式[J].测绘通报,2006,4(5):7-10.
(编辑:张磊)
