振动流化床与浸没水平管平均传热特性理论分析与实验研究*
2012-02-07朱学军
朱学军 ,邓 俊
(1.攀枝花学院 生物与化学工程学院,四川 攀枝花 617000;2.攀枝花市化工资源有效利用重点实验室,四川 攀枝花 617000)
流化床的一个显著特征就是床层温度均匀和具有较高的传热效率,这使它对于一系列的反应,特别是具有高放热效率的放热反应特别适应,同样由于浸没管表面可以向床内移入和移除热量,所以在各工业部门中已获得了广泛应用。
在流化床内设置热交换管束,管内通入蒸气或其它加热介质,利用管壁表面与流化床层间高的传热速率,向床内施加补充热量,从而提高流化床干燥器的热效率及干燥能力。通过浸没表面提供的热量可以占到总供热的80%甚至更高,考虑气体供热和浸没加热管供热的平均效率可达90%,从而热能消耗可大大降低,可实现干燥过程得高效节能[1]。
近年来,关于流化床与浸没水平换热管的传热实验研究非常活跃,在很多方面都取得了重大突破,这方面的专业文献也很丰富[2-4]。但不同研究者所得出的计算式相差很大,而且各个关联式适应范围不同,即仅在各自的实验条件下才能很好地相符合。由于影响流化床传热的因素很多,到目前仍没有一个适用于整个流化床的传热关联式。
关于振动流化床与浸没表面的传热模型主要是通过固定式流化床与浸没表面间的传热模型修正得来的。Ringer and Mujumdar认为对于传统流化床传热系数在u>umf后增加的原因是更有效的颗粒混和,而对于振动流化床的传热系数还强烈的依靠振动参数和颗粒直径,在垂直振动的流化床中控制合适的振动参数和气速就可以使床内颗粒流动和传热达到最佳,并在不振动流化床传热模型的基础上得到了预测振动流化床传热系数的数学模型。
Pakowski et al通过实验证实,振动对于细小颗粒与浸没表面的传热系数具有较大的影响,能够显著增加传热系数,但对于大颗粒,这种影响的作用将减弱,甚至在某些情况下还会削弱传热,使传热系数反而下降。Mujumdar and Pakowski认为振动的引入,可以强化传热,在较低的通气速度下即可获得较大的传热系数,气流速度仅在u<umf时才对传热系数有较大影响,振动流化床最大传热系数比不振动大10%~20%。
Malhotra and Mujumdar以 dp=0.325~1.017mm的玻璃珠为物料,采用二维振动流化床,研究了振动频率、振幅、气速、颗粒直径和颗粒湿含量等因素对床层与浸没水平圆柱表面平均传热特性的影响。当振幅固定在4.25mm,u/umf=0时,振动可以大大强化传热,表面与床层间传热系数可以提高超过20倍。
本研究以平均粒径为1.83mm的玻璃珠为物料,研究了振动流化床与水平管间的传热规律;考察了气速、振动频率、静床高度、管径等因素对平均传热系数的影响。在颗粒团更新理论基础上建立了颗粒团对流传热系数数学模型、气体对流传热系数关联式,从而得到振动流化床与浸没水平管平均传热模型。比较了传热系数的理论预测值与实验测定值,两者吻合较好,从而验证了提出的传热模型的正确性。
1 传热模型建立
对于振动流化床,由于机械振动的引入将影响床层颗粒的流化状态。影响床层与浸没表面间传热系数的因素还包括振动参数(振动频率和振幅)。所以振动流化床与浸没水平管间的传热比固定式流化床更加复杂,床层与浸没表面间的传热系数可用式(1)表示

式中 f0:气泡分率 /%;hpp、hgc、hb和 hr分别为颗粒团对流传热系数、气体对流传热系数、气泡传热系数和辐射传热系数,W·(m2·K)-1。
振动流化床颗粒床层与浸没水平管表面传热物理模型见图1[5]。通过建立物理模型可以得到颗粒团对流传热系数计算式和气体对流传热系数计算式。

图1 水平管传热物理模型Fig.1 The heat transfer model of horizontal tubes

其中气体对流传热系数由式(2)计算,颗粒团对流传热系数通过式(3)计算。管壁平均传热系数have可采用局部时均传热系数的面积平均来计算。

2 传热特性实验装置及原理
图2为振动流化床传热特性实验装置示意图。实验用振动流化床为240×80mm2的二维流化床。为便于观察床内物料运动状态,床体由透明有机玻璃制成。分布板采用开孔率为4.9%、孔径为2mm的多孔板。其上铺设一层100目的不锈钢丝网以使气流均布,振动流化床床体通过四根金属弹簧支撑在固定支架上,床体通过导向连杆与一偏心机构相连接,偏心装置通过皮带与调速电机相连。借助偏心装置的作用,将电机的旋转运动转换成床体在竖直方向上的往复运动。导向连杆上装有直线运动轴承,保证床体仅沿竖直方向运动,克服水平方向上的摆动。振幅可通过改变偏心距来调节,振动频率则通过调节调速电机的转速加以控制,并通过数字式光电转速表测出。气体由鼓风机通过孔板流量计计量后由床底进入。

图2 平均传热系数测试实验装置示意图Fig.2 Schematic diagram of the experimental system
测量传热系数的水平管如图3所示。在直径25 mm、长60 mm的铜棒同心嵌入一长为60 mm,直径为4 mm的加热棒,棒体两端用聚四氟乙烯端头封住,在铜体表面焊接铜-康铜热电偶,热电偶引线从表面内侧穿过端头引出。水平管两端固定在床壁上。水平管轴线距气体分布板60 mm,对称安装在床的中心位置,床层温度由安装在水平管下方距气体分布板20 mm处的裸露热电偶测定。实验时,将流化气速调节至一定值,并使流化床按一定的振幅和频率进行振动,接通加热电源,实验持续到微元面的温度稳定不变时,测得微元管壁温度和床层温度,即可按式(5)计算平均传热系数h。

图3 平均传热系数测试探头Fig.3 Test probe of the average heat transfer coefficient

式中 h:传热系数,W·(m2·K)-1;Q:通入水平管的热量,J·s-1;A:水平管测试部位面积,m2;tw:管壁温度,℃;tB:床层温度,℃。
3 结果与分析
3.1 振动频率的影响
图4、5比较了水平管直径为25mm,床高为95mm时不同振动频率和流化气速的条件下平均传热系数理论预测值与实验测定值之间的关系。

图4 平均传热系数理论计算值与实验值的比较Fig.4 Comparison of experimental values of the average heat transfer coefficient with calculated values(f=6.7Hz,H0=95 mm)

图5 平均传热系数理论计算值与实验值的比较Fig.5 Comparison of experimental values of the average heat transfer coefficient with calculated values(f=11.2 Hz,H0=95 mm)
从图4、5中可以看出,实验值和理论预测值虽有差异,但差别较小。在各种振动频率下流化数较小时理论预测值和实验值吻合较好;在较高流化数、低振动频率时,实验值处于理论值上方;随着振动频率增大,平均传热系数实验值逐渐趋于理论预测值甚至低于理论预测值。这主要由于振动频率和流化数大时,床内气泡分率增加,所以传热系数降低,但理论预测值中假定气泡传热与气体传热系数相当,所以预测值偏大。
3.2 床高对平均传热系数的影响
图6比较了水平管直径为25mm、床高为130mm、振动频率为11.2Hz的条件下平均传热系数理论预测值与实验测定值之间的差异。

图6 平均传热系数理论计算值与实验值的比较Fig.6 Comparison of experimental values of the average heat transfer coefficient with calculated values(f=11.2 Hz,H0=130 mm)
从图6可以看出,理论预测值低于实验值,可能是在理论模型中单纯考虑了床高增加将削弱传热,也就是床高加高,振动能量衰减得越快,振动的强化作用越不明显,床高增加颗粒流化质量变差的缘故,但在实际实验中,气体的分布,特别是气体通过水平管时的流动状态对传热具有较大的影响,如果在管壁附近位置流化质量好于其它位置,则可能使实验获得的传热系数高于理论预测值。
3.3 管径对平均传热系数的影响
图7比较了水平管直径为32mm、床高为95mm、振动频率为11.2Hz的条件下平均传热系数理论预测值与实验测定值之间的差异。
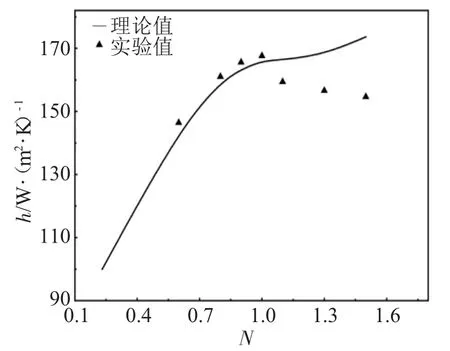
图7 平均传热系数理论计算值与实验值的比较Fig.7 Comparison of experimental values of the average heat transfer coefficient with calculated values(f=11.2Hz,Dt=32mm,H0=95 mm)
从图7可以看出,在流化数小于1.0时理论预测值小于实验值,流化数大于1.0时理论预测值大于实验值。这可能是由于流化数小时,管背风面未流化的颗粒更多,传热减慢;高流化数条件下这层颗粒厚度减薄,而在理论模型中考虑的是管径对迎风面气膜和背风面颗粒层的平均影响,所以理论预测与实验值会有一定的差异。
3.4 理论预测与实验值的比较
图8示出了不同条件下部分实验数据与理论预测值间的比较,所取数据点个数为80。

图8 平均传热系数理论预测值与实验值的比较Fig.8 Comparison of experimental values of the average heat transfer coefficient with calculated values
从图8可以看出,两者吻合较好,实验值与理论预测值间的误差在±15%以内,表明本研究提出的计算颗粒床层与水平管间的平均传热系数数学模型是可靠的。
4 结论
(1)在各种振动频率下流化数较小时理论预测值和实验值吻合较好;在较高流化数、低振动频率时,实验值处于理论值上方;随着振动频率增大,平均传热系数实验值逐渐趋于理论预测值甚至低于理论预测值。
(2)水平管管径增加,在流化数小于1.0时理论预测值小于实验值,流化数大于1.0时理论预测值大于实验值。
(3)通过对振动流化床与浸没水平管间传热特性分析,在颗粒团模型的基础上,建立了平均传热数学模型,并与实验测定的值进行了比较,实验结果与模型预测较为一致,表明本研究建立的传热模型能正确揭示振动流化床与浸没水平管间的传热规律,对传热系数能进行很好的预测。
[1]叶世超.振动流化床水平换热管传热特性研究[D].四川大学,2000.
[2]N.S.Grewal.Heat transfer between immersed horizontal tubes and bubblingfluidized beds[J].Trends in Chemical Engineering,1994,2(1):33-58.
[3]S.W.Jim,J.Y.Ahn,S.D.Kim.Heat transfer and bubble characteristics in a fluidized bed with immersed horizontal tube bundle[J].International of Heat and Mass Transfer,2003,46(4):399-409.
[4]S.Rasouli,M.R.Golriz,A.A.Hamidi.Effect ofannular fins on heat transfer of a horizontal immersed tube in bubbling fluidized beds[J].Power Technology,2005,154(5):9-13.
[5]ZHU Xuejun,YE Shichao,PAN Xiaoheng.The local heat transfer mathematical model between vibrated fluidized beds and horizontal tubes[J].Experimental Thermal and Fluid Science,2008,32(6):1279-1286.
