新建船队的船队优化模型建立和比较

刘宝涛 王运龙 陈 明

大连理工大学船舶CAD 工程中心，辽宁大连116024

0 引 言

在已知运输需求的情况下规划新组建船队的配置和规模，满足任务要求并期望获得最大收益是航运企业常需面临的现实课题。

在有多条航线和多种可用型船且各港口供需量已知的情况下确定船队的最佳构成，关键在于优化模型的建立。连续变量线性规划模型和混合整数线性规划模型是解决船队规划问题最常用的模型，具有模型简单、计算方便的优点，但也存在着船舶调度的现实合理性问题。有些企业从便于管理的角度出发，要求单船固定一条航线，此时，就需要采用整数规划模型来解决这一类问题。但整数规划计算复杂，相关研究也开展得较少［1］。

本文针对具体的新建船队的规划问题，全面考虑了现役船舶的运输能力及其营运数据等条件，根据航运企业不同的需求侧重点，建立了连续变量线性规划模型、混合整数线性规划模型和整数规划模型，均是以船队必要运费率为目标函数，获得可信的优化结果。

1 问题描述

船队承担运输任务的航区由一级和二级两类港组成，货物由海外先运输卸载到一级港，然后再向二级港转运。一级港中有若干个港口兼作调峰港，可通过接收其他一级港送来的货物来应对需求高峰，其关系如图1 所示。

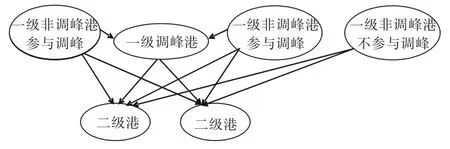
图1 航线示意图Fig.1 Sailing route diagram

具体条件为：

1）共有K 种船型可供选择。

2）航区内有G 条可能航线；一级港M 个，其中调峰港口L 个，非调峰港不参与调峰的港口P个；二级港N 个。

3）以预测的未来某年营运需求为基础数据。

4）假定船舶使用寿命为Y年，折算出的每年的营运费用相同。

同时，要求船队必须满足二级港和一级调峰港的需求，各二级港的需求量和一级港的最大提供量等条件已知。

针对上述问题，建立以Y年内的必要运费率为目标函数，考虑运量、时间等约束条件的优化模型。必要运费率是确保不亏损的最低单位货量的运费。若必要运费率低于市场运价，则该方案可以接受。必要运费率越低，方案越具有竞争力，承担的风险也越小［2］。

2 数学模型的建立

2.1 连续变量的线性规划模型

连续变量的线性规划模型，不仅简单，而且运算方便。此模型有一个假设前提，即船舶以简单航次的形式运行，在装货港一次性装满货物出发，航行至卸货港后一次性卸空货物。解此模型，当求得的某型船在某航线上的配置艘数是小数时，说明该船并非全年都在该航线上营运，还有一部分时间在其他航线上营运。而对于每年的建船量而言，则必须圆整为整数值给出。圆整后的最优解值可能会发生一点变化，但只要目标函数值的变化不大，仍认为它是优解（或称其为次优解）［3-5］。

模型建立为：

式中，Xtij为从第t个港口装货到第i个港口卸货的航线上第j种船型的数量；Pj为第j种船型的船价，万元；Rtij为从第t个港口装货到第i个港口卸货的航线上第j 种船型的年营运费用，万元；W 为各航线各种船型的年总运量，万吨；IY为现值因数。

约束条件如下：

1）港口供需约束。

一级非调峰港参与调峰的港口供应约束：

其他一级港的供应约束：

二级港的需求约束：

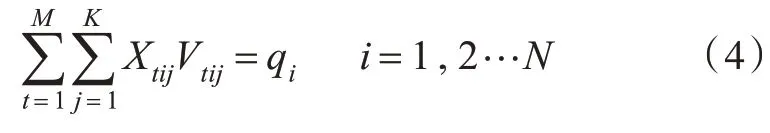
一级调峰港的需求约束：

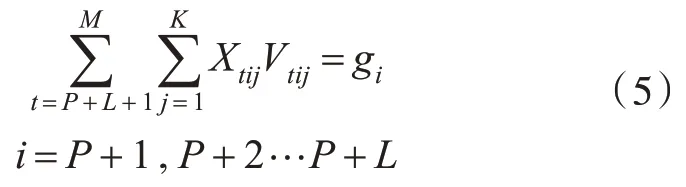
在使用其他3 种模型时，需求约束中的“=”改为“≥”。

2）港口时间约束。

一级非调峰港参与调峰的港口的时间约束：

一级非调峰港不参与调峰的港口的时间约束：

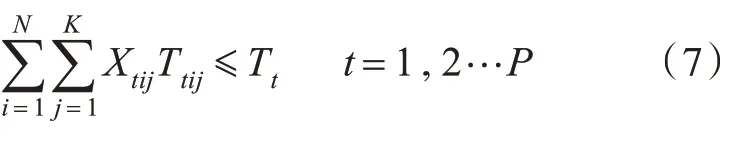
二级港的时间约束：

一级调峰港的时间约束：

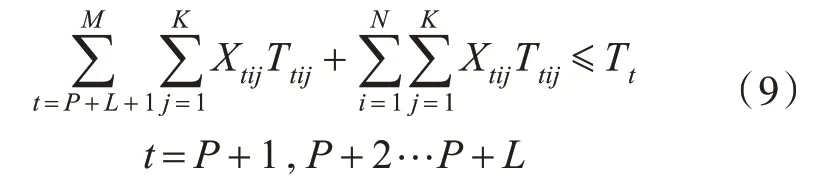
3）非负性约束。

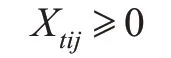
其中，Vtij为从第t个港口装货到第i个港口卸货的航线上第j 种船型的年营运力，万吨；Qt为第t个一级港的最大外输量，万吨；qi为第i个二级港的需求量，万吨；gi为第i 个一级调峰港在需求高峰时的需求量，万吨；Xtij为从第t 个港口装货到第i 个港口卸货的航线上第j 种船型的年靠港时间，天；Tt为第t 个一级港一年所能提供的最大停靠时间，天；TTi为第i 个二级港一年所能提供的最大停靠时间，天。

在该模型中，共有K×(L×(M-L-P)+M×N)个变量。求解后，就可得到最优航线和最佳船型。

2.2 混合整数模型

与连续变量的线性规划模型相比，混合整数模型增加了所有航线中任意一种船型数量的和一定是整数的约束［6］，这使得计算出的船舶数量一定是整数，就没有线性规划中的圆整问题了［7-9］。

与前一模型的目标函数表达式相同，在原有约束的基础上加上了每一种船型的船舶数是整数的约束。

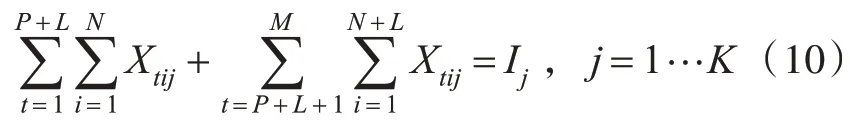
式中，Ij为整数。与前一模型相比，此模型增加了j个变量和j个约束。

2.3 整数规划模型

与前2 类模型相比，整数规划模型增加了约束，使计算出的每条航线的船舶数量一定是整数，即每条船运营1 条航线。下面，将分别讨论线性整数规划模型和非线性整数规划模型。

2.3.1 线性整数规划

线性整数规划的目标函数与上面的模型一致，在原有约束的基础上添加了每条航线上每种类型船的数量一定为整数的约束，即Xtij∈{0，1，2，…} 。

此模型得出的结果并不一定是最优解，实际上往往是次优解，其原因是，运量和时间约束中的系数是某船型以简单航次形式运行1年的年运力和年占港时间。而在实际情况中，船舶的运输能力往往未被全部利用，即实际上的年运输量要小于年运力，年实际占港时间也小于年最大占港时间，这就有可能导致某条最优的航线被排除。例如，某港口的供应约束为：

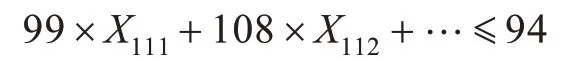
根据约束，当X111等于1、其他值等于0 时，是不满足约束的。但实际上，这也能完成运输任务，只是船舶的利用率未达到100%而已，这就有可能排除了较优的航线和船型。针对模型的这个缺陷，可以通过在模型约束中添加利用率系数，进行多次试算来找出一个比较优的解。

如假设利用率系数为0.8，约束变为：

99×0.8×X11+108×0.8×X12+…≥94

然后，再进行优化计算。计算时，可以多试几个利用率系数，然后比较优化结果并从中找出较好的解。可以认为，这个解是比较优的。

2.3.2 非线性的整数模型

通过建立非线性的数学模型，可以避免线性整数优化模型的缺陷，具体做法是，将单船年营运费用分为固定费用C1和变动费用C2，固定费用是1年中不变的费用，比如年船员费用、保险费、港口管理费等；变动费用包括燃油费、拖航费等随航次数变化而变动的费用。可以假设从第t 个装货港出发的第i 条航线第j种船型船的实际年运量（变量）为Qtij，然后，根据这条航线上此种船的航次运货量（已知）来确定航次数，因此，变动费用可表示为实际年运量的函数。通过整理发现，该函数关系是一次的，即C2=f(Qtij)。然后，便可得出从第t 个港口装货到第i 个港口卸货的航线上第j种船型的单船年实际费用C0=C1+C2=F(Qtij)，是Qtij的一次函数。

所建模型为：

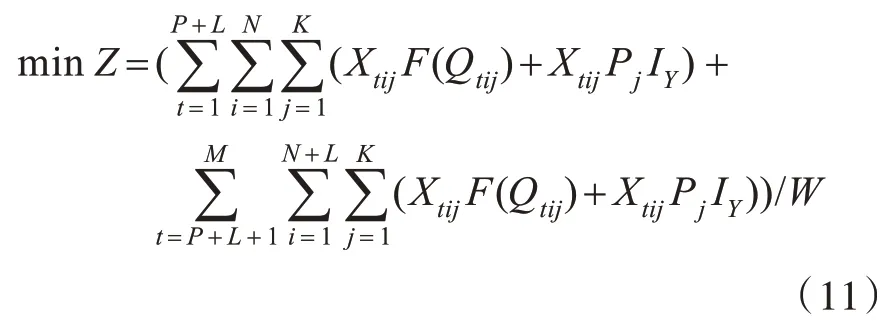
约束条件如下：

1）港口供需约束。

一级非调峰港参与调峰的港口的供应约束：

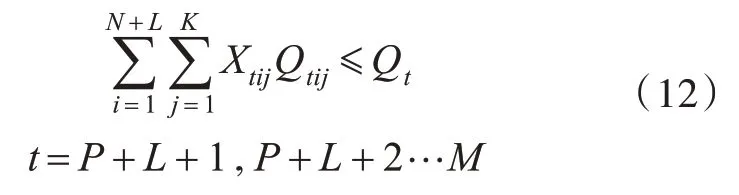
其他一级港的供应约束：

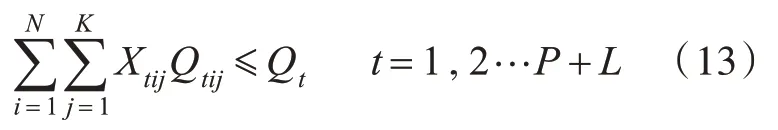
二级港的需求约束：

一级调峰港的需求约束：

2）港口时间约束。

一级非调峰港参与调峰的港口的时间约束：

一级非调峰港不参与调峰的港口的时间约束：

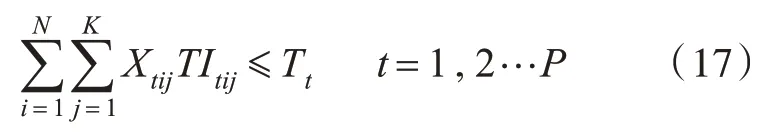
二级港的时间约束：

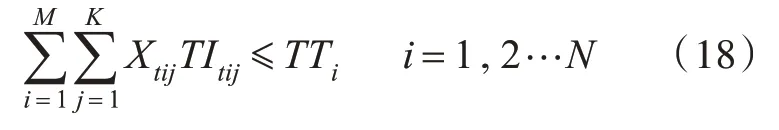
一级调峰港的时间约束：

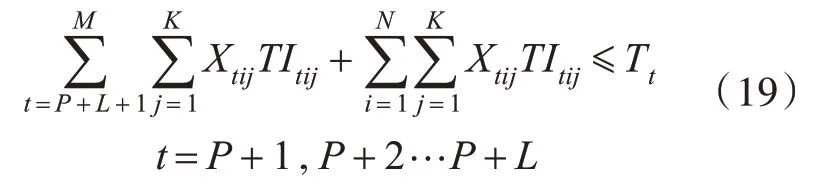
3）变量关系，单船的实际运量和实际的占港时间也是线性关系。

4）每条航线上的每种船型必须为整数，即Xtij∈{0，1，2，…} 。

5）非负性约束。

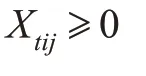
其中，Qtij为从第t 个港口装货到第i 个港口卸货的航线上第j种船型的实际年运量，万吨；TItij为从第t个港口装货到第i个港口卸货的航线上第j 种船型的年实际靠港时间，天；Qt为第t 个一级港的最大外输量，万吨；qi为第i 个二级港的需求量，万吨；gi为第i 个一级调峰港在需求高峰时的需求量，万吨；Tt为第t 个一级港一年所能提供的最大停靠时间，天；TTi为第i 个二级港一年所能提供的最大停靠时间，天。

在该模型中，共有3×K×（L×（M-L-P）+M×N）个变量。该模型求解的是一个非线性约束优化问题，这种问题的解法是人们最为关心的，因此研究的人较多，提供的方法也较多，但目前尚没有一种对一切问题都普遍有效的算法，而且求得的解也多是局部最优解。但本模型的结果依然具有重要的参考作用［10］。

3 计算实例

某公司现在要组建运输船队，有6 个一级港，（其中1 个调峰港），4 个二级港。其中，有3 个一级港有余量向调峰港运输，分别为一级港1、一级港2、一级港5。共有4 种船型，港口供需量、运距、各船型、年运力、航运量、航次占港时间均已知，试确定某一年的最佳航线最佳船型。

3.1 已知条件

1）船型信息。总共有4 种不同舱容的船型可以选择，分别为（2×104），（3×104），（4×104），（8×104）m3，造价分别假设为48 000 万 元、61 000 万元、79 000 万元和91 000 万元。

2）航线运距（n mile），如表1 所示。

3）各航线各船型年营运费用，万元。

4）各航线各船型单船年运力，万吨。

5）单次航行一级港小船的停靠时间，天。

6）单次航行船舶在二级港的停靠时间，天。

7）各港口需求量、供应量（万吨）和营运时间（天）如表2 所示。

限于篇幅，不一一列出第3）～6）的信息表格。

表1 航线运距Tab.1 Sailing distances among different ports

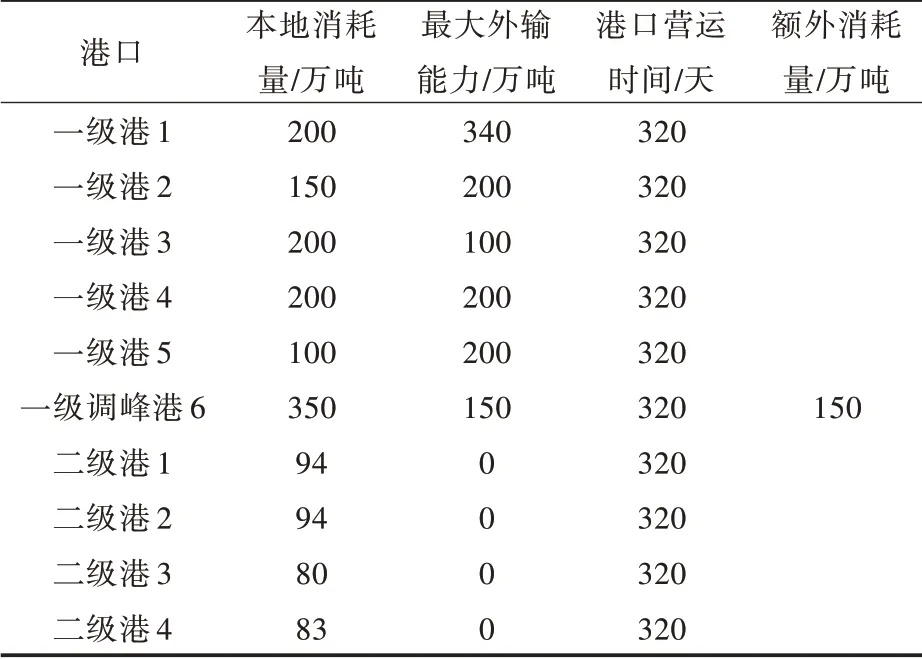
表2 港口需求信息Tab.2 Demand information from each port

3.2 计算结果与比较

根据以上信息，可计算出各模型的的结果，如表3 所示。

线性模型得到的最优值为Z=46.5 元/t；混合整数线性模型得到的最优值为Z=58 元/t，其中4种不同舱容的船的数量分别为I1=1，I2=0，I3=0，I4=2；线性整数模型得到的最优值为Z=85.3 元/t；非线性整数模型得到的最优值为Z=90.1 元/t。

根据上述结果可以看出，最优的航线距离往往比较短，最佳的船型往往比较大。这样的结果是合理的，此外，4种优化模型的建模也比较方便。

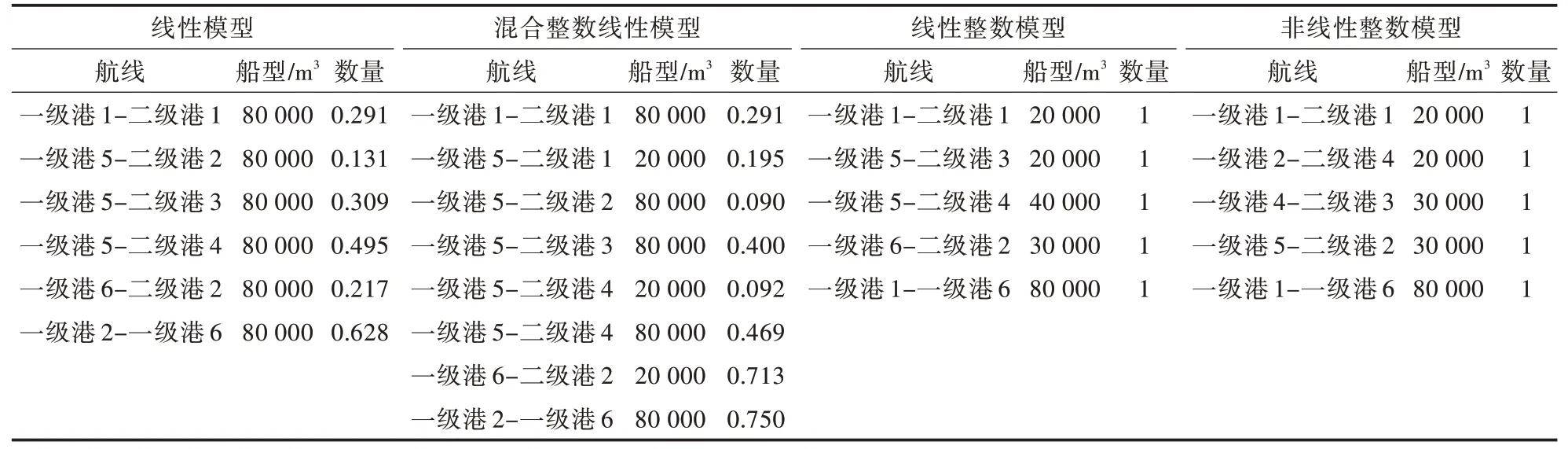
表3 不同模型的优化计算结果Tab.3 Computational results by different models

比较4 个模型的最优值可以看出，线性规划最优值最小（圆整前），但其船舶数目不是整数，需要圆整；而线性混合整数规划的结果虽然不需要圆整，但线性规划与线性混合整数规划都存在调度管理的问题；对于整数规划模型的结果，船舶数目肯定是整数，且每条船只在单一航线上行驶，不存在上述模型的问题，但最优值比较大。从中可以看出，船舶调度管理与经济性之间存在着矛盾，至于选哪种新组建船队的模型，应根据企业的实际情况决定。

4 结 论

本文以一个具体的新组建船队问题建立了4种优化模型，得出以下结论：

1）连续变量的线性模型或混合整数线性模型所得到的营运方案的优点是经济性比较好，缺点是这2 种模型的结果都需要船舶调度，往往需要1 艘船营运于几条航线，这可能会给航运管理带来不便，由于一些原因，有些调度可能也不能实现。

2）整数模型得到的方案的优点是营运方案为单船单航线，管理方便，缺点是经济性比前2 种模型的营运方案差。此外，值得说明的是，对于本文所建的整数模型，往往只能得到局部最优解，但经过对线性整数模型的多次试算并与非线性整数规划模型的结果进行比较取优，依然能够得到较好的结果。

上述结果对于企业结合具体情况选择合适的优化模型具有一定的参考价值。

［1］谢新连. 船舶调度与船队规划方法［M］. 北京：人民交通出版社，2000.

［2］谢新连.船队规划的动态模型与算法［J］.中国造船，1992，45（3）：102-110.XIE X L.A dynamic model and algorithm for fleet plan⁃ning［J］.Shipbuiding of China，1992，45（3）：102-110.

［3］纪卓尚，谢新连，李树范. 沿海原油运输船队规划［J］.船舶工程，1993，15（2）：17-21.JI Z S，XIE X L，LI S F.A theoretical study on the plan⁃ning of Chinese coastal crude oil carrier fleet［J］. Ship Engineering，1993，15（2）：17-21.

［4］杨秋平，谢新连，苏晨. 航线配船与船队规划模型及算法实现［J］.中国航海，2009，32（1）：91-95.YANG Q P，XIE X L，SU C. Model of ship routing and fleet planning and its algorithm［J］. Navigation of Chi⁃na，2009，32（1）：91-95.

［5］张鲁峰，张仁颐.发展我国巨型油船船队的战略规划［J］.上海交通大学学报，2001，35（12）：1873-1876.ZHANG L F，ZHANG R Y. Strategic scheme for VLCC fleet development of China［J］. Journal of Shanghai Ji⁃ao Tong University，2001，35（12）：1873-1876.

［6］谢新连，李树范，纪卓尚，等.船队规划的线性模型研究与应用［J］.中国造船，1989，42（3）：61-68.XIE X L，LI S F，JI Z S，et al. Study and application on-the linear model of fleet planning［J］. Shipbuilding of China，1989，42（3）：61-68.

［7］JARAMILLO D I，PERAKIS A N.Fleet deployment op⁃timization for liner shipping part II：implementation and results［J］. Maritime Policy and Management，1991，18（4）：235-262.

［8］CHO S C，PERAKIS A N. Optimal liner fleet routeing strategies［J］. Maritime Policy and Management，1996，23（3）：249-259.

［9］PERAKIS A N，BREMER W M. An operational tanker scheduling optimization system：background，current practice and model formulation［J］.Maritime Policy and Management，1992，19（3）：177-187.

［10］唐焕文，秦学志. 实用最优化方法［M］. 大连：大连理工大学出版社，2004.