基于响应面法的强力甲板结构优化设计

黄重阳 林 焰，2 于雁云，2

1 大连理工大学船舶工程学院船舶CAD 工程中心，辽宁大连116024

2 工业装备结构分析国家重点实验室，辽宁大连116024

0 引 言

当散货船空载航行时，为保持适当的稳心高度、避免产生过大的船体弯矩、剪切力及振动，常要在压载舱内注入压载水。然而，在压载工况下，除重压载舱注满了压载水外，其余货舱均为空，顶边舱的局部横向载荷与中拱状态下的总纵弯矩便一同作用于船体。因此，船体中部货舱强力甲板的剧烈弯曲变形便会导致其总纵强度被削减［1］。可见，强力甲板的设计是否合理直接关系到船舶营运的安全性与经济性。

在船体结构的优化设计中，设计变量（结构尺寸）与结构的应力等响应存在着复杂的关系，很难用弹性力学理论推导出某种显式函数，因而使得对设计约束（强度、刚度）或设计目标的计算变得困难。虽然运用有限元法可解决复杂结构的强度计算问题，但是需要耗费大量的时间，在结构优化迭代过程中不断调用有限元分析程序，这样的设计计算既不经济又不实用。

本文结合有限元法与响应面法［2］，将首先对一艘76 000 DWT 散货船货舱段的强力甲板（在不同板厚、相同工况下）进行灵敏度分析，并选取适合的厚度参数作为响应面函数的自变量，然后应用大型通用有限元软件计算出最大相当应力后，运用响应面法的均匀设计试验方法得出该舱段强力甲板最大应力与结构厚度的响应面函数，继而以结构重量最轻为目标函数，以强度和规范要求的最小厚度为约束条件，对该货舱段的强力甲板结构厚度进行优化。

1 响应面法

响应面法（RSM）是试验设计与数理统计学分析相结合的综合试验技术，用于处理几个变量对一个系统或结构的影响问题，因而被广泛用于众多领域。

上世纪50年代，响应面法便被运用于化学工业，用于确定最优的操作过程［3］。在生物学上，响应面法主要用于研究混合反应物中各化学反应成分所占比例与其生物学活性之间的关系，以便确定生物材料最优的试验条件［4］。在结构工程领域，响应面法主要被应用于结构优化设计和可靠性分析等方面，其作为一种近似的计算方法，在过去的十几年中得到了迅速的发展和应用［5-6］。目前，我国已有研究人员将响应面法用于大型船舶的中剖面结构优化中，但还只是初步尝试，其中，有的学者简化了船舶有限元模型的横向构件，忽略了纵向骨材，仅考虑纯扭转这一种工况而未选取结构最危险的工况。

1.1 响应面法的原理

响应面法的基本原理是：首先假设一个包含未知系数的、由状态变量与基本变量构成的解析表达式，然后用拟合的方法确定未知系数以表达隐式函数或高度非线性函数。多项式系数的确定一般以试验设计为基础，应用正交设计或均匀设计回归得到特定因子的最小二乘估计。采用此方法时，随机变量的个数越多，试验次数便越多。

在结构力学分析领域，响应面函数模型常采用二阶多项式形式：

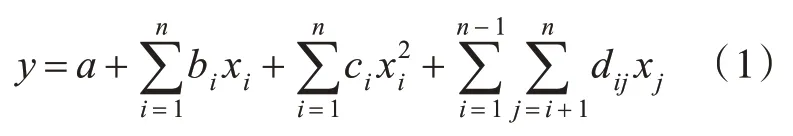
式中，a，bi，ci，di为待定系数；xi（i＝1，2，…n）为基本变量。为简化计算、节省时间、避免限制响应面法的应用范围，本文根据文献［7］和文献［8］保留了常数项、一阶项及二阶平方项，舍去了二阶交叉项，采用以下形式：

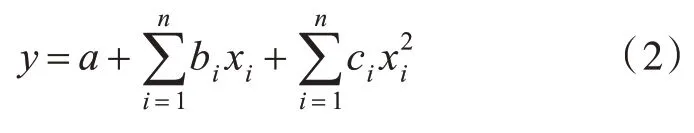
响应面法用二次多项式代替大型复杂结构的极限状态函数，并通过系数迭代进行调整，一般都能满足实际工程的精度要求，具有较高的效率和使用价值。

1.2 基于响应面的结构分析及优化

通常的结构优化设计主要是着眼于重量最轻等目标，并借助基于梯度信息的传统数值优化方法直接进行寻优，而高精度结构有限元分析模型的引入则使得计算时间变长，且在约束条件较多的情况下不利于寻优，往往容易陷入局部最优解。探索型优化技术（如模拟退火算法、蚁群算法、遗传算法等）在全局搜索中往往要对目标函数值进行大量的计算评估，无法针对具体工况下的受力特征合理、精确地优化具体结构，且计算规模也不易控制［9］，这对于借有限元法计算的目标值（如应力响应、寿命响应）而言，计算代价过大。

为解决上述问题，本文借助试验设计方法和响应面近似模型技术建立了结构优化设计方法，其基本思想是：在规范设计方法的指导下选取结构的设计变量，利用灵敏度分析方法选取对结构响应影响较大的样本点［10］，对舱段结构建立有限元模型并进行结构分析，得到对应各样本点的响应（弯曲应力），利用这些样本点和响应值，建立应力的响应面近似模型，从而避免在寻优过程中进行大量耗时的有限元建模与分析。

1.3 试验设计方法

响应面法的计算成本随样本点向量维数的增加而快速增长，其拟合能力很大程度上受样本点试验空间分布的影响。当样本点向量维数很大时，首先要进行灵敏度分析和试验设计，对样本点的合理选择十分重要。目前，用于优化领域的试验设计方法［11］主要有正交设计和均匀设计。

为兼顾时间和拟合精度，本文采用均匀设计试验安排响应面试验。试验所考察的结果称为指标，如结构的最大剪应力、最大相当应力、最大位移等。对指标可能有影响的参数称为因素，如结构的几何尺寸、材质等。各因素用于比较的具体条件称为水平，如几何尺寸的不同取值。

2 构造结构响应面模型

2.1 舱段有限元模型的建立

以一艘76 000 DWT 散货船为例，其总共有9个货舱，总长243.80 m，两柱间长235.00 m，型宽32.20 m，型深19.50 m，设计吃水12.50 m，结构吃水14.00 m，方型系数0.887，航速约为14.20 kn。

按照中国船级社的相关规范［12］，建立船体中部6 号货舱（125～153 号肋位）的舱段模型，并施加相应的边界条件及载荷，如图1 所示。为了尽量消除边界条件的影响，本文仅以模型中部整舱段的强力甲板（AH32 高强度钢）作为研究对象。该舱强力甲板的最大受力情况出现在轻压载工况，相当应力云图如图2 所示。由图可见，强力甲板的应力分布是不均匀的。在压载工况下，货舱范围内靠近横舱壁上方的强力甲板的受力显著大于其他区域。根据结构强度计算对甲板厚度进行优化设计，不仅能提高船舶安全性，而且还可降低船舶的结构重量。

图1 舱段有限元模型Fig.1 Finite element model of cargo holds

图2 强力甲板应力云图Fig.2 Stress contours of strength deck

2.2 均匀试验分析

船体结构复杂，影响构件强度的参数众多，为能更合理地构造响应面函数，本文针对该舱段强力甲板应力最大的压载工况，对不同受力区域、不同厚度的强力甲板进行了敏感度分析。对于大型散货船，强力甲板的板厚主要取决于压载工况。甲板初始设计结构图如图3 所示。本着基于母型、不增加焊缝的原则，确定设计参数，各参数所代表的区域如表1 所示。选取对强度影响较大的参数作为响应面函数中的自变量。分析方法是，保持其他参数不变，只变化其中某一参数，然后利用有限元软件计算、分析此参数的变化对最大相当应力的影响。

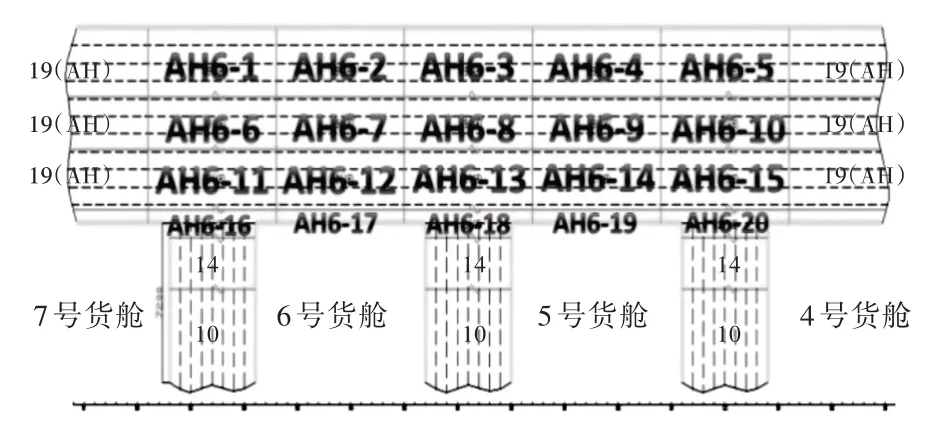
图3 甲板结构图Fig.3 Structural plan of deck

表1 设计变量及所代表的区域Tab.1 Design variables and their representative areas

通过参数化建模、变换板厚尺寸并进行试验后，对参数进行敏感度分析，选择敏感度较大的AH6-8 号甲板板厚x6、AH6-11号甲板板厚x7、AH6-13 号甲板板厚x9、AH6-16 号甲板板厚x10和AH6-18 号甲板板厚x12作为自变量。

以减少试验次数为原则［13］，采用均匀设计试验法安排响应面试验。本文选用不含交叉项的二次多项式作为响应面方程，其中参数为5 个，方程的未知数为11 个（方程未知数个数等于2n＋1），16 水平5 参数的正交试验需进行16 次。试验结果如表2 所示。

利用最小二乘法拟合响应面函数：

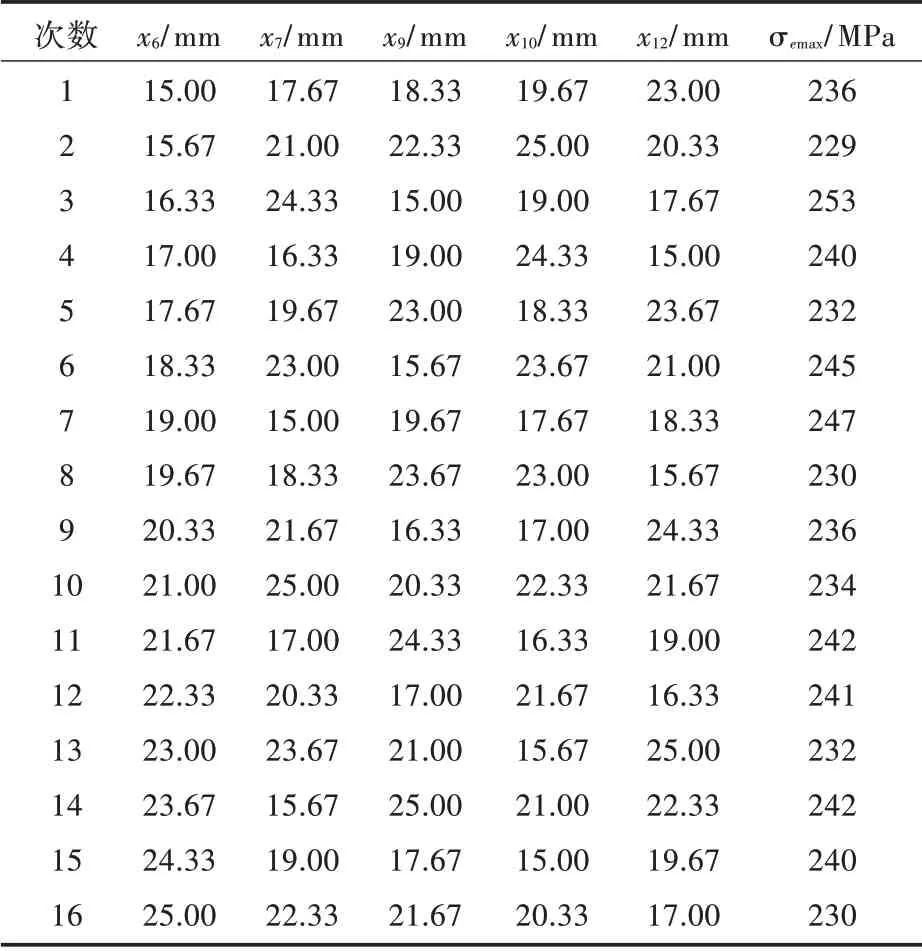
表2 均匀试验表Tab．2 Experimental data table of uniform design

式中，ye为最大相当应力的响应值。

根据复相关系数评估公式

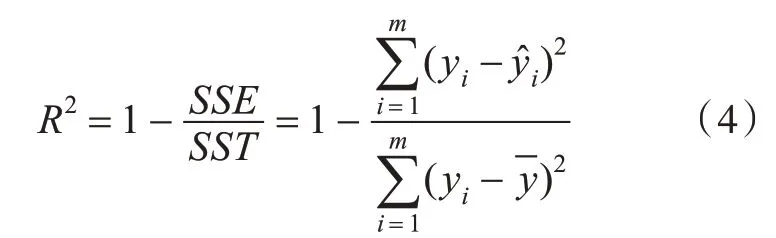
进行拟合度评估，得出各响应面函数的R2为0.991 825。

由拟合度评价指标可看出，本文中通过试验拟合的强力甲板强度响应面的拟合度高，即响应面相对于实际模拟得比较好，为下一步进行优化提供了良好的基础。

3 优化设计

强力甲板为AH32 高强度钢，许用应力为282 MPa。为了消除结构强度冗余，本文引入值为1.2的安全系数，使得最大相当应力响应面函数可起到约束目标函数的作用，并保证结构优化后的结果偏于安全。根据回归方程的二次多项式及相关规范［14］要求，以强力甲板结构质量最轻为目标，可建立如下优化模型：

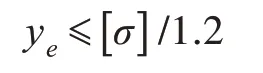
式中，xi为板厚，mm；Ai为表面积，m2；P 为密度，t/m3；[σ ]为许用应力，N/mm2。

使用非线性整数优化的分支定界法对优化模型进行求解，将各区域的强力甲板厚度作为离散变量进行优化，优化结果如表3 及图4 所示。

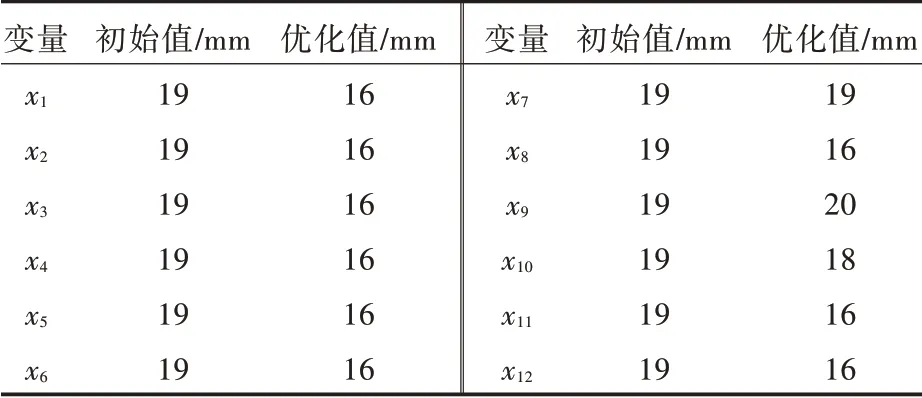
表3 强力甲板设计变量优化结果Tab．3 Optimization results of strength deck

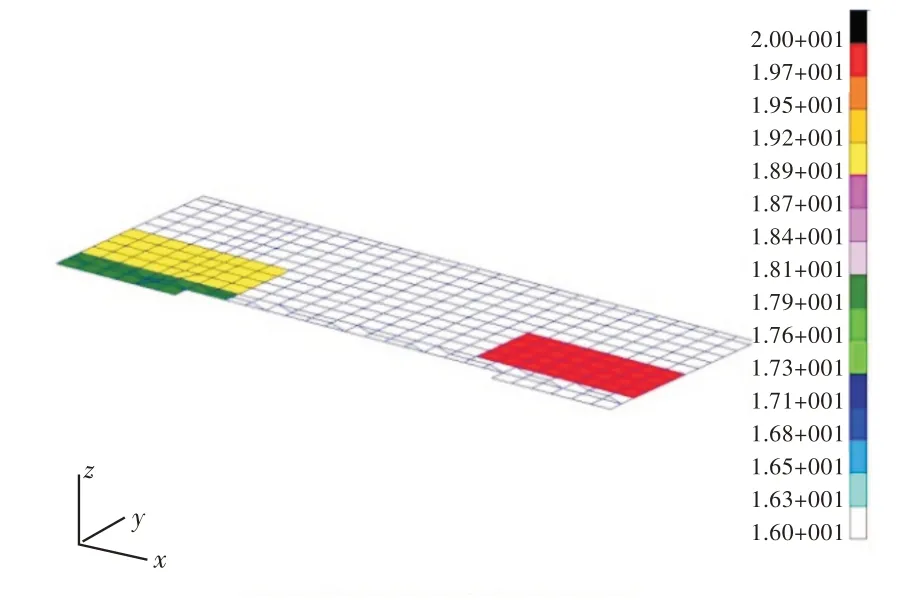
图4 优化后的甲板厚度Fig.4 Thickness of optimized deck

原始重量为39.071 2 t，优化重量为34.858 0 t，优化后，重量较实际设计减小了10.78%。

使用优化后的板厚对模型重新建模，计算得到最大相当应力245 MPa（图5），满足规范要求。

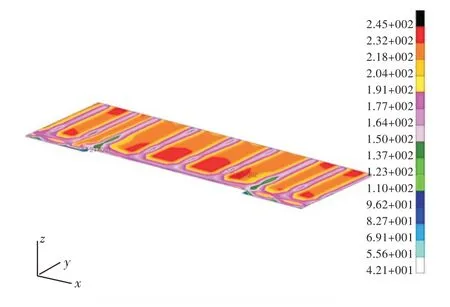
图5 优化后的应力云图Fig.5 Stress contours of optimized strength deck

通过优化结果及验证结果可以看出，利用大型通用有限元软件和响应面法探讨散货船舱段强力甲板的结构优化问题，其计算结果合理可信，说明该方法是可行的。

4 结 论

1）提出了一种基于响应面的船体结构优化方法，首次将响应面法和有限元法应用到散货船强力甲板结构优化计算中，并针对不同受力区域的甲板板厚进行优化，验证了该方法的实用性，开拓了船舶结构强度分析以及结构优化的新思路。

2）首先对不同受力区域的甲板厚度参数进行敏感性分析，合理选择构造响应面函数的自变量，而后运用均匀试验的方法设计试验，最后通过最小二乘法拟合成响应面函数。该函数能够模拟散货船强力甲板在压载工况下的应力状态，为进一步构造船体响应面提供了参考。

3）构建了散货船整舱段的强力甲板结构优化模型。该优化模型以该货舱段强力甲板的重量最轻为设计目标，以不同区域的甲板厚度为设计变量，以总纵弯曲产生的最大弯曲应力及相关规范要求为约束条件。优化结果显示，该优化设计方法减轻了强力甲板的重量，说明其在实际工程中具有一定的应用价值。

4）该方法具有一定的通用性，响应面函数的拟合与结构具体形式无关，因而可以应用于大多数散货船的典型结构优化设计中。

［1］HUANG C Y，LIN Y，YU Y Y. M/V‘Hebei Mercy’bulk carrier structural strength direct calculation report［R］.Plan Approval Center，CCS，2010．

［2］黄重阳. 基于响应面法的散货船结构优化设计［D］.大连：大连理工大学，2011．

［3］HILL W J，HUNTER W G. A Review of response sur⁃face methodology：A literature review［J］. Technomet⁃rics，1966，8（5）：571-590.

［4］MEAD R，PIKE D J. A review of response surface methodology from a biometrics viewpoint［J］. Biomet⁃rics，1975，31（12）：803-851.

［5］ROUX W J，STANDER N，HAFTKA R T. Response surface approximations for structural optimization［J］.International Journal for Numerical Methods in Engi⁃neering，1998，42（3）：517-534．

［6］佟晓利，赵国藩.一种与结构可靠度分析几何法相结合的响应面方法［J］.土木工程学报，1997，30（4）：51-57.TONG X L，ZHAO G F. The response surface method in conjunction with geometric method in structural reli⁃ability analysis［J］. China Civil Engineering Journal，1997，30（4）：51-57.

［7］刘洁雪. 基于响应面法的集装箱船优化设计研究［D］.天津：天津大学，2008.LIU J X. Research on optimum design of a container ship based on response surface methodology［D］. Tian⁃jin：Tianjin University，2008.

［8］杨书仪，刘德，文泽军. 基于响应面法的桥梁主桁架结构优化设计［J］.机械设计，2007，24（6）：14-16.YANG S Y，LIU D，WEN Z J. Structural optimization design of bridge main truss based on method of re⁃sponse surface［J］. Journal of Machine Design，2007，24（6）：14-16.

［9］MAKOTO A，TAITO S，TATSUHIRO S. Optimization of transverse bulkhead design by response surface methodology［J］. Journal of the Kansai Society of Naval Architects，2000，234：237-243.

［10］王永菲，王成国. 响应面法的理论与应用［J］. 中央民族大学学报（自然科学版），2005，14（3）：236-240.WANG Y F，WANG C G. The application of response surface methodology［J］. Journal of The Central Uni⁃versity For Nationalities（Natural Science Edition），2005，14（3）：236-240．

［11］邓苗毅，任伟新. 基于响应面方法的结构有限元模型修正研究进展［J］.铁道科学与工程学报，2008，5（4）：42-45.DENG M Y，REN W X. Study on structure finite ele⁃ment model updating based on response surface meth⁃odology［J］. Journal of Railway Science and Engineer⁃ing，2008，5（4）：42-45.

［12］中国船级社. 散货船结构强度直接计算分析指南［S］.北京：人民交通出版社，2003．

［13］隋允康，张立新，杜家政.基于响应面方法的桁架截面敏度分析和优化［J］. 力学季刊，2006，27（1）：96-102.SUI Y K，ZHANG L X，DU J Z. Sensitivity analysis and cross sectional optimization of truss structure us⁃ing response surface methodology［J］. Chinese Quar⁃terly Mechanics，2006，27（1）：96-102.

［14］中国船级社. 钢质海船入级规范［S］. 北京：人民交通出版社，2009.