轧管机环形孔型工作段曲线设计及应用
2012-02-02苗国伟
苗国伟
(中铝洛阳铜业有限公司,河南洛阳471039)
20世纪90年代随着带有环形孔型及曲面芯棒的两辊周期式轧管机的兴起,半圆形和马蹄形孔型逐渐趋于消失,环形孔型及曲面芯棒配合的轧制曲线,延长了工作行程长度,使得孔型及芯棒受力得以分散,提高了孔型及芯棒的寿命,并且提高了轧制加工率,使得轧机的工作效率得到提高,产量大幅增加。环形孔型及与之相配的曲面芯棒是两辊周期式轧管机的核心工具,其设计的正确合理直接关系到轧管机的生产效率、产品质量以及工具自身的寿命,对应半圆形和马蹄形孔型环形孔型的设计更为复杂,计算时必须用计算机进行辅助设计,否则计算的工作量非常繁重。本文重点介绍了孔型及芯棒工作段的曲线设计,并使用计算机编程进行了实例计算。
1 孔型工作段轧槽顶部曲线直径及芯棒曲线的计算公式(环形孔型轧槽展开示意图见图1)
1.1 孔型工作段轧槽顶部曲线直径的计算公式
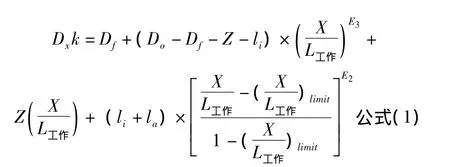
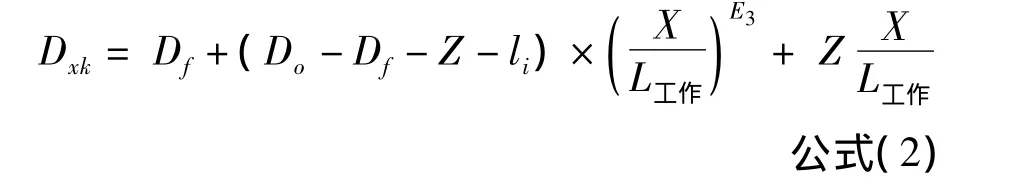
式中Dxk—— 轧槽工作段“X”点处轧槽顶部直径,mm
Df——成品管外径,mm
Do——管坯外径,mm
Z——芯棒要求的最小锥度
Z=Z相×(L工作/100) 公式(3)
式中L工作——轧槽工作段长度,mm
Z相——相对最小锥度,以0.25%进行计算
li——管坯内径与芯棒之间的间隙,mm
la——在X/L工作=1处轧槽顶部与管坯外径之间的间隙
X/L工作——轧槽工作段“X”点处与工作段长度L的比值
E2——孔型间隙指数,对铜及铜合金通常取E2= 2.0
E3——孔型指数,对铜及铜合金通常取E3=2.5
(X/L工作)limit——随E2变化的极值,对铜及铜合金通常取值为0.7
1.2 芯棒曲线的计算公式
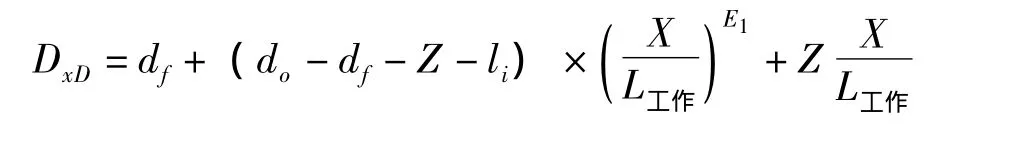

式中DxD——“X”点处的芯棒直径,mm
do——管坯内径,mm
df——成品管内径,mm
Z——芯棒要求的最小锥度
li——管坯内径与芯棒之间的间隙,mm
X/L工作——轧槽工作段“X”点处与工作段长度L的比值
E1——芯棒指数,对铜及铜合金通常取E1=2.5
从以上孔型及芯棒曲线的计算公式中可以看出,孔型工作段轧槽顶部直径的变化与管子的内径无关,孔型指数E3决定减径量;而芯棒工作段直径的变化与管坯、成品管的外径无关。
2 孔型工作段轧槽开口宽度Bkw的计算
孔型的轧槽曲线确定后,对于孔型孔槽设计还需要确定轧槽的开口宽度,因为管坯在每次送进后,工作锥的直径比与之对应的孔型轧槽顶部直径大,因此必须在孔型孔槽侧壁留有适当余量Fx,以容纳因管子送进产生局部体积增量,避免轧制时出现耳子,造成成品料表面飞边,影响产品质量。影响孔型孔槽开口宽度的因素有送进量、孔型轧槽顶部曲线和芯棒曲线(见图2)。

图2 孔型轧槽断面示意图
孔型工作段轧槽开口宽度Bkw的计算公式:

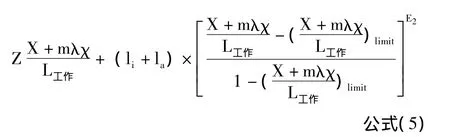
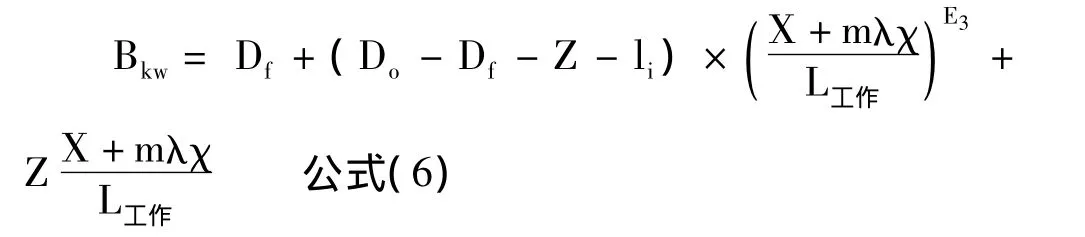
式中m——送进量,mm
λx——计算断面的延伸系数,等于管坯与计算断面管子的断面面积之比

在实际制造过程中,孔型轧槽两侧的边部应加工一定的圆角,以保证孔型轧槽开口处的圆滑过渡。
3 孔型工作段轧槽的实例计算
孔型工作段轧槽尺寸及芯棒直径实例计算。已知轧机轧制坯料为φ80×10mm,轧制成品规格φ42× 2.2mm,送进量为12mm,孔型工作段长度为600mm。
3.1 孔型工作段轧槽尺寸及芯棒直径所要求计算的数据
①孔型孔槽顶部直径Dxk。

公式(10)
③孔型孔槽开口宽度Bkw。
④芯棒工作段直径Dxo。
3.2 要精确计算以上的数据,需将轧槽工作段分成40段进行计算
计算数据非常庞大,本例采用计算机编程来实现,采用Foxpro编写了程序。
为了编写程序简单化,先对上述一些公式中相关固定的数据进行简化:
①Z=Z相×(L工作/100)=0.25%×(600/100)= 0.015。

③根据经验确定li=3mm,la=2mm。
④已知Do=80mm、do=60mm、D5=42mm、d5= 37.6mm、h=12、E1=2.5、E2=3.0、

3.3 程序运算结果如表1
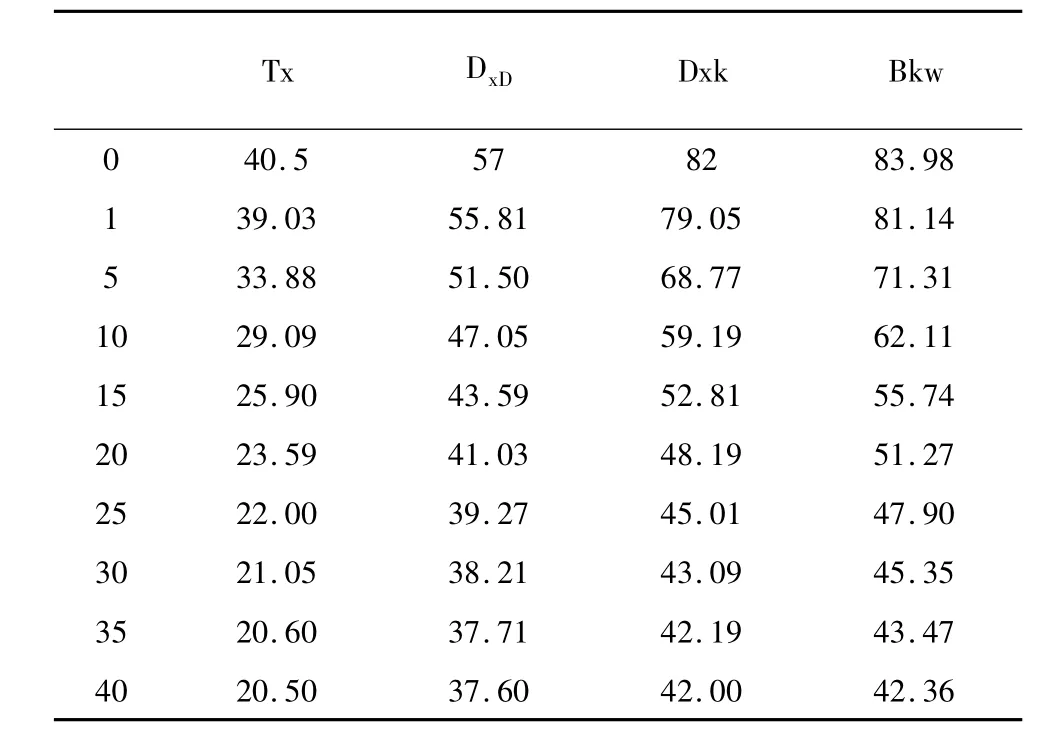
表1
4 结论
①孔型工作段轧槽顶部直径只与管坯、成品管的外径有关,而与内径无关;
②芯棒工作段直径的变化与管坯、成品管的内径有关,而与外径无关;
③孔型工作段轧槽开口宽度只与管坯、成品管的外径及送进量有关;
④根据前节的计算公式及程序,只要知道管坯及成品管的内外径尺寸、工作段长度、送进量,即可以迅速的得出孔型工作段轧槽顶部直径(Dxk)、孔型工作段轧槽开口宽度(Bkw)、芯棒工作段直径(DxD)等相关数据,为孔型的制造单位以及使用单位提供了设计及检测的依据。
[1]钟卫佳主编《铜及铜合金加工手册》,北京,冶金工业出版社,2007.1
