落体法测量刚体转动惯量实验中引起测量值偏离的因素分析
2012-02-01王海林司嵘嵘李相银
王海林,司嵘嵘,李相银
(南京理工大学物理实验中心,江苏南京210094)
1 引 言
如何使目前高等院校的物理实验课程适应培养创新型人才是十分重大的研究课题[1].物理实验教学是理工科院校本科生重要的基础课程,是大学生进入高校最早必修课程之一,课程内容丰富、时间长、涉及专业广.在近几年的物理实验教学中,我们提出并实践了“层次—递进—素质互联一体化”的教学新模式,探索着如何培养学生科学实验素质、提高学生实验创新能力、满足不同层次不同专业学生对物理实验课程的需求,该研究工作内容涉及到课程体系、内容、教学方法、教材等[2-4],其中对一些传统的必修实验进行实验内容和方法的改进和延伸是一种最简单、方便的方法[5-6].刚体转动惯量测量是许多高校学生必修的基础性物理实验[7],转动惯量测量有多种方法,如落体(动力)法、扭摆法(三线扭摆、单线扭摆)和复摆法等.本文并讨论了落体法测量刚体转动惯量中拉绳与转轴不垂直情况下对刚体转动惯量的影响,测量并分析了转动体在阻力矩作用下的角加速度与转速的关系.该内容作为刚体转动惯量实验的拓展性、创新性实验内容,有利于启发学生实验思维和培养学生实验创新意识,有利于激发学生的个性发展和对实验的兴趣,提高学生独立思考和分析数据的能力,进而提高了教学效果.
2 实验原理
落体法测量刚体转动惯量实验装置如图1所示,刚体转动体系受到2个力矩,一个是细绳的拉力矩M=Tr,r为绕线塔轮的半径,T≈mg为细绳的拉力(刚体转动体系的质量远远大于砝码质量时,可忽略砝码下落时的加速度的影响);另一个是转动体系受到的阻力矩Mμ,主要由转轴轴承处的摩擦力矩和转动时的空气阻力矩构成.
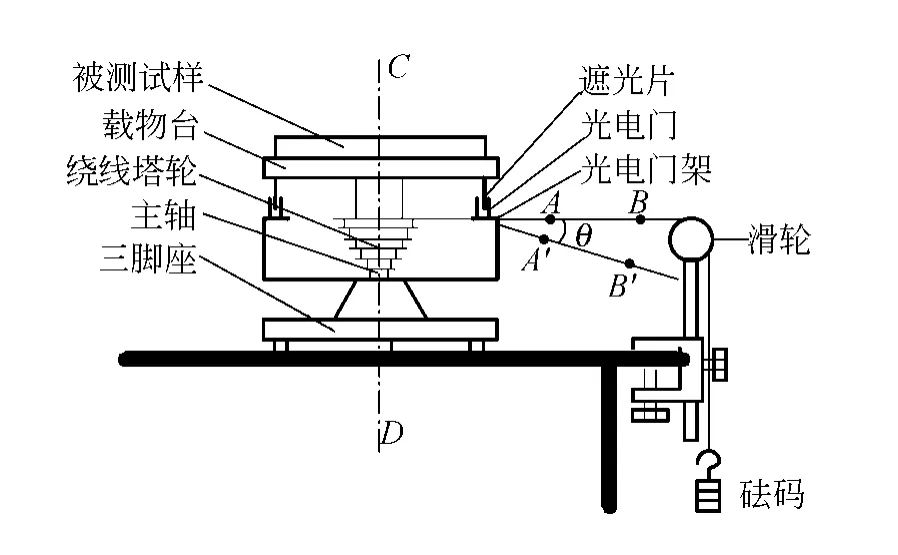
图1 落体法转动惯量测量仪
落体法测量刚体转动惯量所依据的原理为转动定律,即绕定轴转动的刚体的角加速度β与它所受的合外力矩M成正比,与刚体的转动惯量J成反比,即考虑到实验仪器中刚体转动时受到细绳拉力矩M和阻力矩Mμ的共同作用,测量的刚体转动惯量为


式中:m为砝码质量,r为塔轮上绕线轮的半径,β为M和Mμ共同作用下的角加速度分量,βμ为Mμ作用下的角加速度分量.使用式(2)时一定要在实验过程中使拉绳AB与转轴CD垂直.如实验中拉绳AB与转轴CD不垂直,如图1所示,A′B′与AB成θ角,这时转动体系受到细绳拉力矩的水平分量为M=mgrcosθ(由于砝码质量远小于转动体系质量,且实际操作中θ一般较小,因此细绳作用力的垂直分量mgsinθ对阻尼力矩的影响可以忽略),刚体转动惯量计算公式应为

实验过程中如果没有考虑θ的影响,都可以使用式(2)进行计算.如存在θ的影响,由此引起转动惯量测量值的的绝对偏离ΔJ和相对偏离E分别为
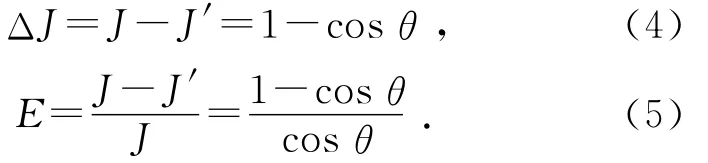
3 测量与分析
3.1 E与θ的关系
表1为θ不同的情况下测量的仪器承物台转动惯量J,使用式(2)计算转动惯量J,从测量值和理论值两方面给出了不同角度θ情况下转动惯量的相对偏离E.实验中m=4.000×10-2kg,g=9.794m/s2,r=2.500×10-2m.
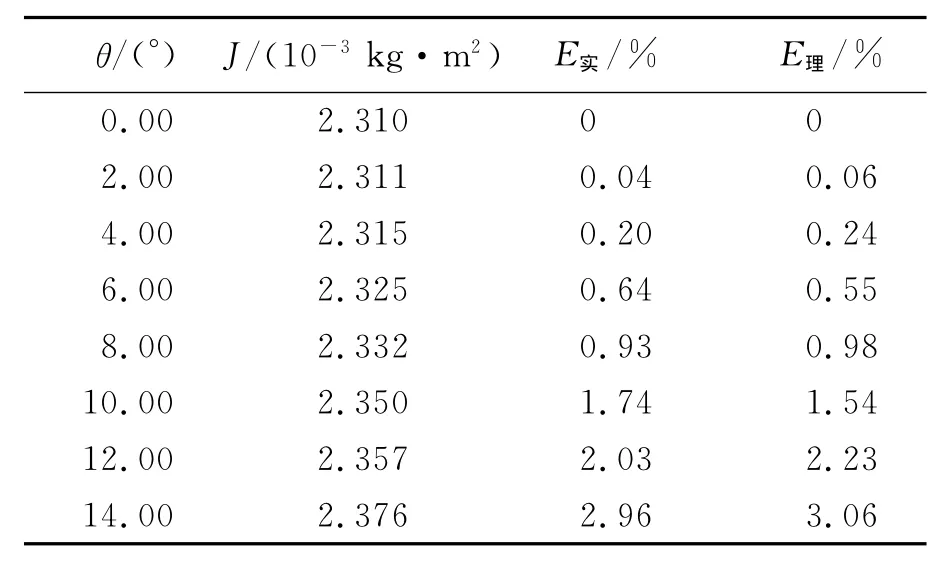
表1 E与θ的关系
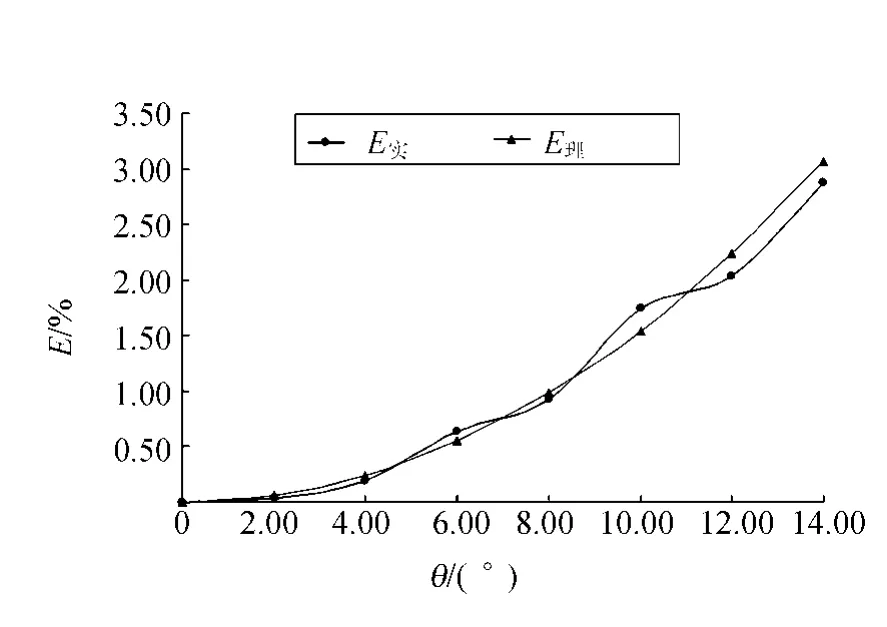
图2 E与θ的关系曲线
由表1中的数据及图2可以看出,由θ变化引起相对偏离实验测量值与由式(5)计算的理论值吻合较好,学生在调节实仪器时必须使θ<5°,否则会带来较大的转动惯量测量值偏离.
3.2 βμ与角速度ω关系
转动惯量测量实验中,并没有考虑βμ与角速度ω关系,认为转动体系所受到的阻力矩Mμ基本上是不变的.实际上转动体系在转动过程中所受到的阻力矩Mμ主要来自于转轴轴承处的摩擦力矩和转动体系转动过程中的空气阻力矩,它们都与角速度ω有关,尤其是空气阻力矩与角速度ω有很大关系.实验测得空承物台的βμ1与ω关系、承物台+两圆柱(0.376kg,对称放置)的βμ2与ω关系、承物台+铝环(0.495kg)的βμ3与ω关系数据如表2~4所示,其中tμ1为θ=2π时的数据,tμ2为θ=6π时的数据.实验中m=4.000×10-2kg,g=9.794m/s2,r=2.500×10-2m.图3为βμ1,βμ2,βμ3与角速度ω的关系曲线.
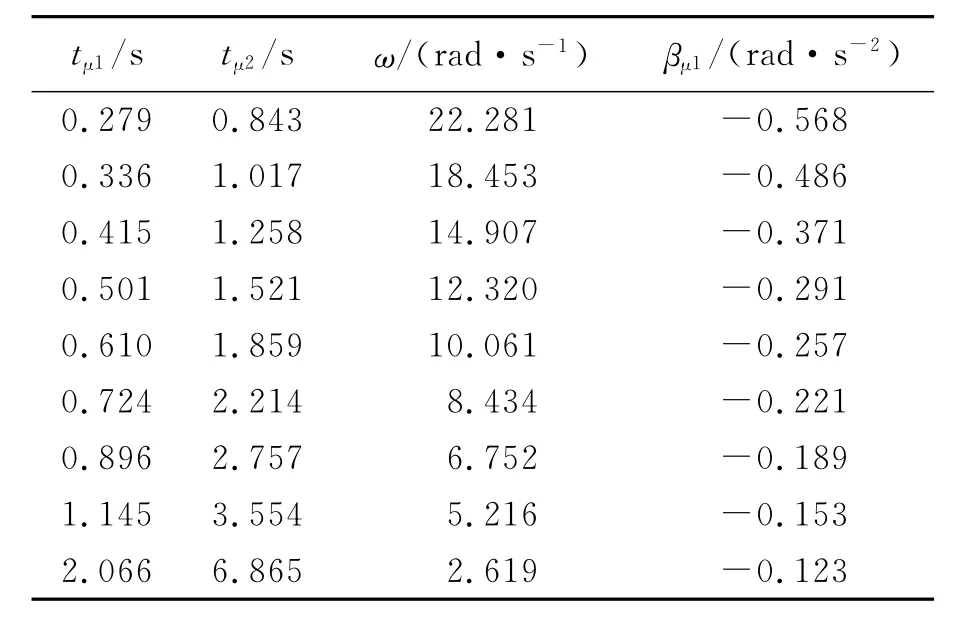
表2 承物台的βμ1与角速度ω关系
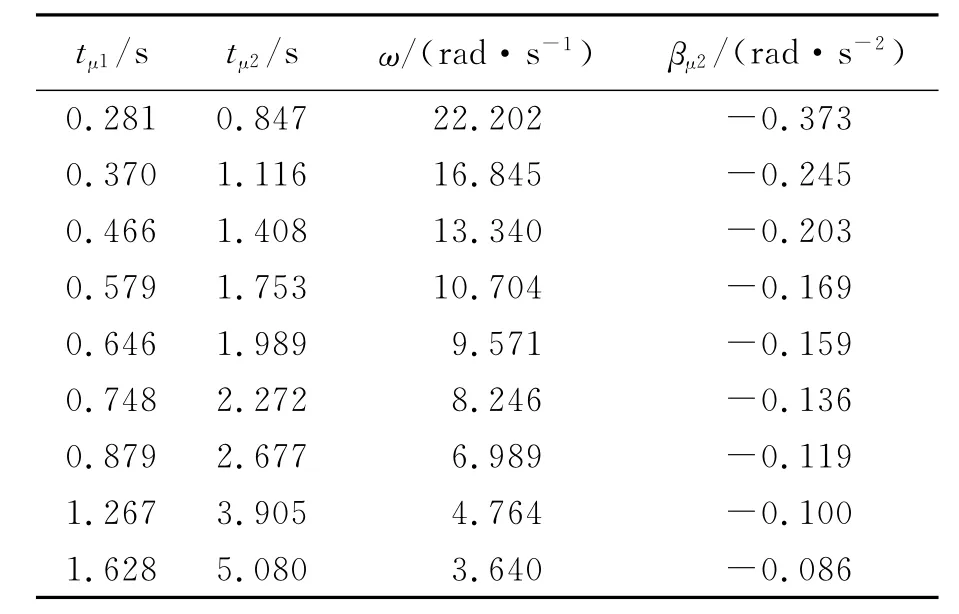
表3 承物台+两圆柱的βμ2与角速度ω关系

表4 承物台+铝环的βμ3与角速度ω关系

图3 βμ与角速度ω关系曲线
从图3可以发现随着ω的增加|βμ|也是增加的,但增加的快慢不同,转动体系质量越小随着ω的增加|βμ|增加越快.βμ与ω关系与转动体系的质量和形状有关.为了减小转动测量误差,测量βμ时转动体的转速应与测量β时差不多.影响βμ的因素来自转动体轴承的摩擦力矩和转动体系转动过程中的空气阻力矩,其中空气阻力矩与角速度ω有很大的关系,且随角速度的增加而增加,这一点与实验测量值相吻合.另外空气阻力矩与转动体系的形状有很大的关系,可进一步进行研究,这是验证转动惯量平行轴定理实验测量数据误差较大的主要原因.
4 结束语
本文对测量刚体转动惯量测量值产生偏离的2个因素进行了深入的分折,可作为刚体转动惯量实验的思考题,以及作为设计性、拓展性、创新性的实验内容,有利于提高学生的学习兴趣、启发学生实验思维和培养学生实验创新意识,有利于挖掘和培养学生内在实验潜质,有利于激发个性发展和对实验产生兴趣,提高学生独立思考和分析数据的能力,提高教学效果.
[1] 教育部高等学校物理学与天文学教学指导委员会.理工科类大学物理实验课程教学基本要求[M].北京:高等教育出版社,2008:1-18.
[2] 赵艳,李相银.分层次、递进式教学全面提高了教学质量,探索物理实验课程对人才培养的新模式[J].物理与工程,2010,20(3):30-32.
[3] 王海林,李相银,杨庆.大学物理实验课程创新性调整及实践[J].南京理工大学学报(社会科学版),2006,19(10):137-139.
[4] 黄淑芳,徐志立.物理实验教学的探讨[J].大学物理实验,2011,24(2):102-103.
[5] 邱菊,严峰,胡国琦,等.旋光仪的改进和实验功能拓展[J].物理实验,2011,31(6):40-42.
[6] 邢键,孙晶华.水中声速的测量[J].物理实验,2011,31(1):34-35.
[7] 李相银,徐永祥,王海林,等.大学物理实验[M].北京:高等教育出版社,2009:93-99.
