包含摩尔-库仑准则的单元劈裂法模拟围压下节理扩展
2012-01-31张振南
杨 帆, 张振南
(1.上海大学土木工程系,上海200072;2.上海交通大学船舶海洋与建筑工程学院,上海200240)
岩体内部含有大量节理,一般在计算时将节理 简化成裂纹.对于节理扩展汇合模式,国内外学者[1-6]已进行了大量的理论与试验研究.对于主要节理,一般采用节理单元法来再现节理面之间的相互作用,其中Goodman类型的节理单元[5]能够很好地模拟节理的力学特性.但是在应用该方法时,有限元网格划分需要事先考虑节理分布和几何形状,以便设置节理单元.另外,在节理扩展时还要重新修正网格,以便设置节理单元,使模拟过程得以继续,这些都给节理扩展过程的数值模拟带来很大不便.为了避免前处理网格划分问题和节理扩展后网格修正问题,张振南等[7-8]提出了单元劈裂法(element partition method,EPM),该方法利用常应变三角单元的几何特点构造了一种特殊的三节点接触单元,用以再现节理面之间的接触和摩擦效应,还可以在原有网格划分方案的基础上直接对裂纹扩展进行模拟,使得节理扩展数值模拟更为简单、高效.目前国际上流行的扩展有限元法(extended finite element method,XFEM)[9-10]也可以在不用重新划分网格的基础上对裂纹扩展进行数值模拟.与EPM相比,XFEM更为精确,但计算过程复杂;而EPM的精确度取决于网格尺寸,计算过程简单,因而为实际工程的预先粗略计算提供了很好的计算手段.
摩尔-库仑(Mohr-Coulomb)准则在岩土工程界是一个广泛使用的破坏准则.当材料微元满足该准则时,微元发生破坏,相当于在微元层面上形成一个裂纹微段.本研究试图以摩尔-库仑准则作为一种单元劈裂准则,应用单元劈裂法对岩体节理扩展行为进行模拟,以探索这种方法在节理扩展模拟过程中的有效性.
1 单元劈裂法
单元劈裂法[7]利用三角单元的几何特点构造特殊的三节点接触单元(见图1),即当有裂纹贯穿时,总有一个节点(节点3)在裂纹的一侧,另外2个节点(节点1和2)在裂纹的另一侧.在裂纹一侧的一个节点可与另外2个节点分别构成2个接触点对.根据这2个接触点对可以推导出三节点接触单元的刚度矩阵[7]为
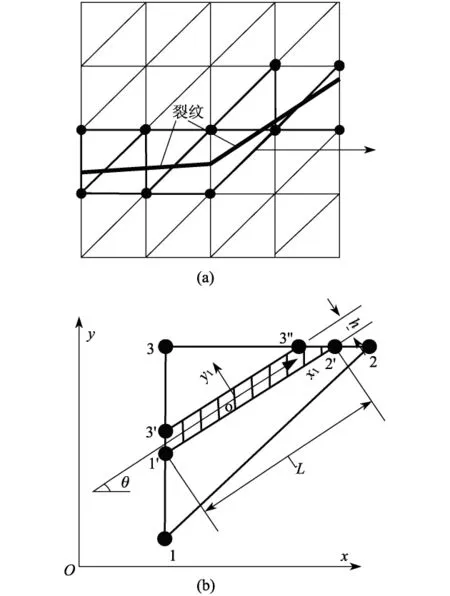
图1 受裂纹切割的单元网格与三节点接触单元Fig.1 Mesh intersected by crack and the tri-node contact element
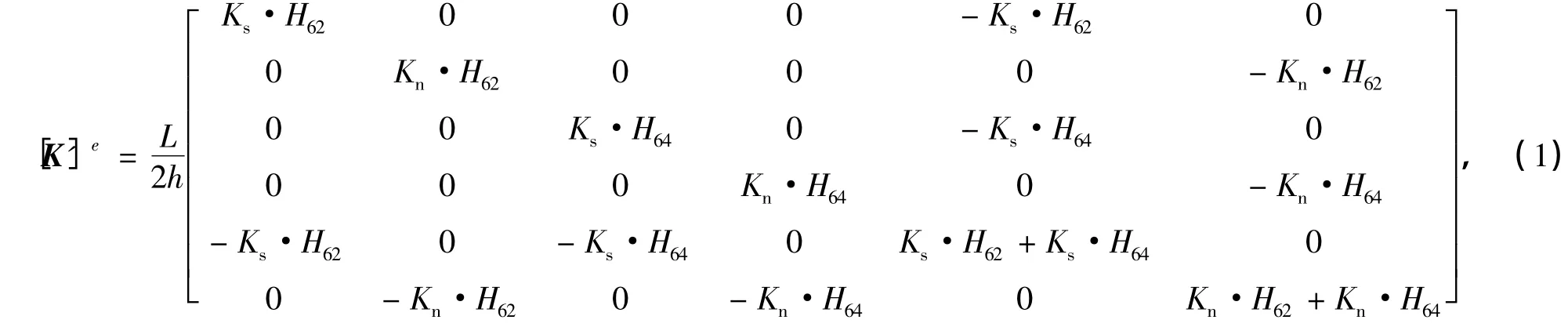
式中,Kn,Ks分别为法向刚度系数和切向刚度系数,L为节理与三角单元相交的长度,h为节理厚度,Hij为表示节理张开与否的参量,
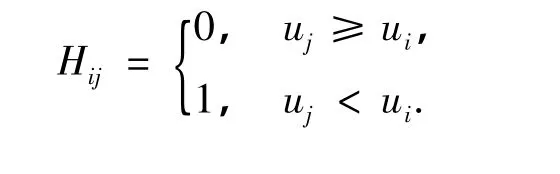
在整体坐标系内,劈裂单元的刚度矩阵可表示为

式中,Q为转换矩阵,
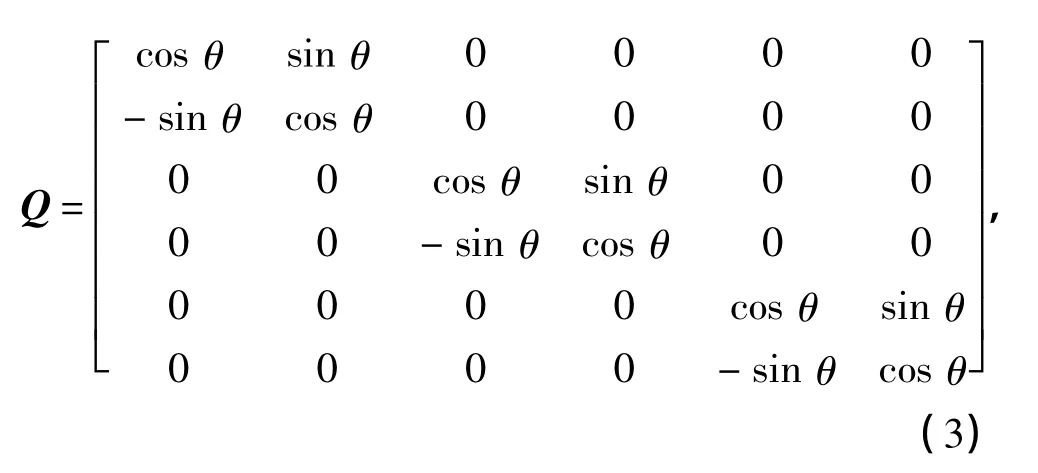
其中θ为节理与坐标轴的夹角.
2 节理力学模型
由于原始节理(即岩石等脆性材料的已有裂隙)间含有填充物,使得节理面之间处于一种弱胶结状态,从而具有一定的黏聚力,如图2所示.节理面何时产生相对滑动取决于节理面之间的黏结强度和作用于节理面的法向和切向应力.在同一节理面内,胶结强度越大,节理面越不容易产生相对滑动;同时,法向应力越大,节理面之间的摩擦应力也越大,就越不容易产生相对滑动.而一旦产生相对滑动, 节理面之间的相对摩擦阻力就会突然降低.为了描述这一过程,采用如下节理面相对滑动准则,即
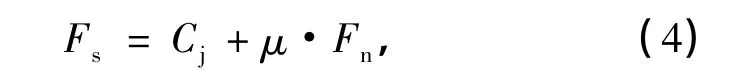
式中,Fs,Fn分别为节理面切向应力和法向应力,Cj为原始节理面内黏聚物黏聚力,μ为节理接触面的摩擦系数.式(4)实质上是摩尔-库仑准则的简单描述形式.
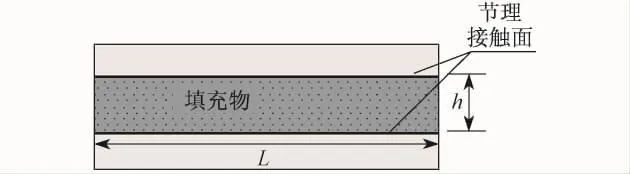
图2 原始节理示意图Fig.2 Illustration of intact joint
在节理面满足滑动准则之前,节理面的切向刚度与法向刚度取相同量级;当节理面满足滑动准则时,节理面法向刚度保持不变,而切向刚度降为0 (或很小量级).因而,原始节理的三节点节理单元刚度矩阵可表示为

式中,
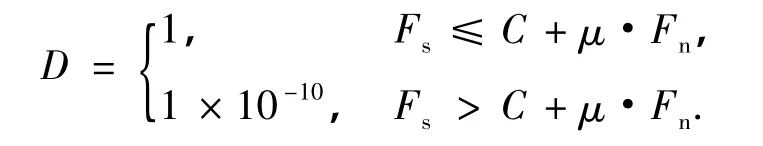
3 节理扩展过程的模拟
节理扩展过程就是节理尖端材料劈裂过程(见图3),在节理尖端取一微元,微元破坏机理可由摩尔-库仑准则来描述.当微元应力状态满足摩尔-库仑准则时,微元发生破坏,形成一个裂纹微段,表现在数值模型上,则为裂尖单元发生劈裂.因而,可以将摩尔-库仑准则作为单元劈裂准则,即
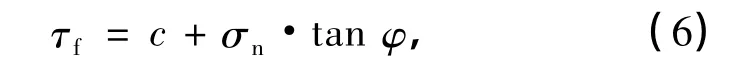
式中,τf为岩体破坏面的抗剪强度,c为岩体黏聚力,σn为垂直破坏面的法向应力,φ为内摩擦角.
本研究假设单元劈裂面垂直于最大主应变ε1方向.同时,为了确定裂纹面的位置,假设滑移面经过三角单元的中心,如图3所示.
4 不同围压下节理扩展数值模拟
4.1 数值模拟参数
为检验本方法的有效性,本研究应用自编的有限单元程序对围压条件下双裂纹扩展进行数值模拟.试件尺寸、裂纹分布模式及试验结果均取自文献[6].试件数值模拟参数如表1所示,尺寸及裂纹分布如图4所示,其中假设岩石破坏前为线弹性.在模拟过程中,采用三节点常应变三角形单元,单元总数为28 282,节点总数为14 400;采用位移控制加载方案,每一荷载步为 0.000 6εt×635=0.160 02× 10-3mm.针对不同的岩桥倾角,每种情况采用0.35,0.70,1.50 MPa 3种不同的围压进行数值模拟.
4.2 0.35 MPa围压下的裂纹扩展分析
图5为倾角β/α=45°/0°时不同荷载步下的裂纹扩展情况.图中可以看出,随着荷载步的增加,试件的外翼裂纹和内翼裂纹从初始裂纹的尖端开始竖直向上扩展;紧接着是次裂纹从初始裂纹尖端顺着初始裂纹方向扩展,最终在岩桥中间位置汇合,贯穿整个岩桥.所模拟的整个裂纹扩展过程与文献[6]中的试验结果基本吻合.
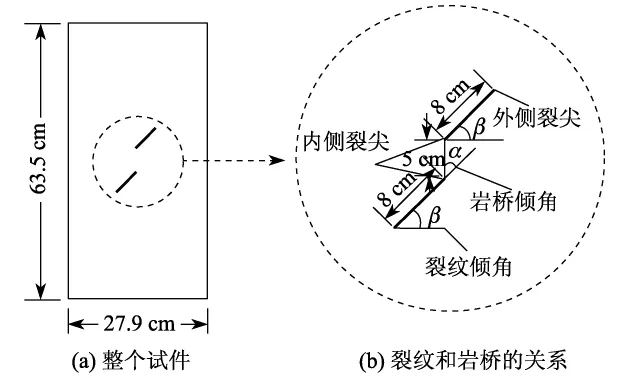
图4 含有预置裂纹的试件[6]Fig.4 Specimen containing pre-existed cracks[6]
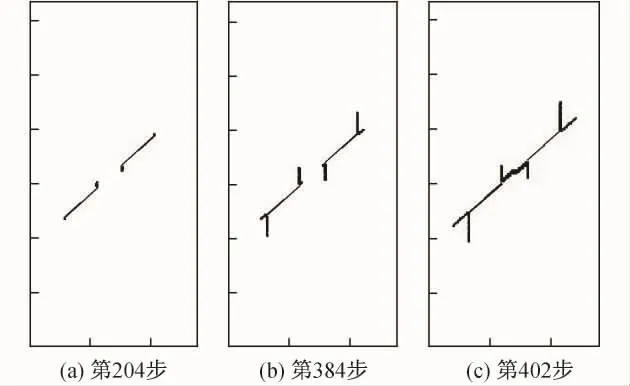
图5 β/α=45°/0°时不同荷载步下的裂纹扩展Fig.5 Fracture propagation at different loading steps when β/α=45°/0°
图6为倾角β/α=45°/30°时不同荷载步下的裂纹扩展情况.图中可以看出,随着荷载步的增加,初始裂纹的2个尖端均出现了向上扩展的翼裂纹.当岩桥区出现次裂纹扩展时,张拉型的内翼裂纹与剪切型的次裂纹发生汇合,连接了初始裂纹的2个内部尖端.由此可见,岩桥区的破坏是由剪切和张拉应力共同作用的结果.
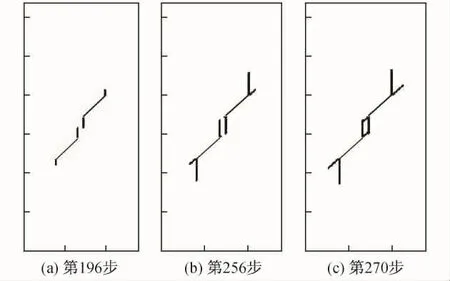
图6 β/α=45°/30°时不同荷载步下的裂纹扩展Fig.6 Fracture propagation at different loading steps when β/α=45°/30°
图7为倾角β/α=45°/45°时不同荷载步下的裂纹扩展情况.同其他倾角情况相似,首先是外翼裂纹向竖直方向扩展,达到一定程度以后,初始裂纹内部尖端的岩桥区出现了内翼裂纹扩展.当内翼汇合后,外翼裂纹继续沿着竖直方向扩展,直至试件最终发生破坏.图8~图10分别为倾角β/α=45°/60°,45°/75°,45°/90°时不同荷载步下的裂纹扩展情况.由图可见,随着荷载步逐渐增加,翼裂纹仍然是最先沿荷载方向扩展,随后在岩桥区产生剪切型裂纹与张拉型裂纹的汇合,从而导致试件最终发生破坏.
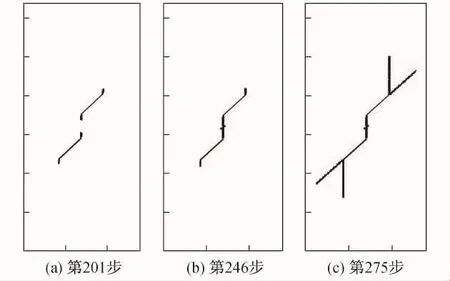
图7 β/α=45°/45°时不同荷载步下的裂纹扩展Fig.7 Fracture propagation at different loading steps when β/α=45°/45°
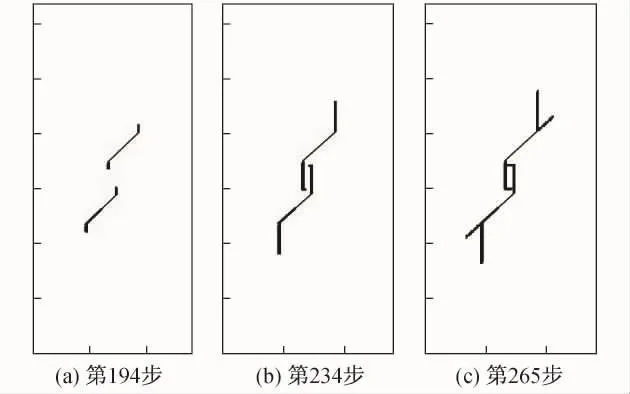
图8 β/α=45°/60°时不同荷载步下的裂纹扩展Fig.8 Fracture propagation at different loading steps when β/α=45°/60°
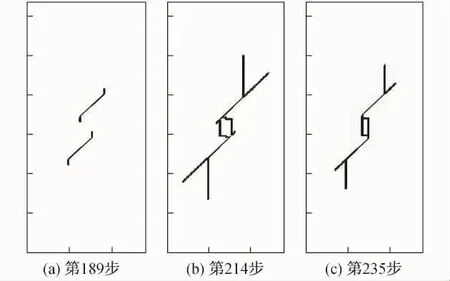
图9 β/α=45°/75°时不同荷载步下的裂纹扩展Fig.9 Fracture propagation at different loading steps when β/α=45°/75°
为了便于将试验结果与模拟结果作对比分析,现将不同岩桥倾角的模拟结果列于图11.从图中可以看出,当岩桥倾角大于0°时,岩桥出现了剪切裂纹汇合(即原有裂纹的内侧裂尖顺着原有裂纹方向产生剪切裂纹汇合)和张拉裂纹汇合(即在岩桥区内产生竖直方向的裂纹汇合).总体上看,试验所得的裂纹扩展模式和数值模拟所得的裂纹扩展模式基本一致.
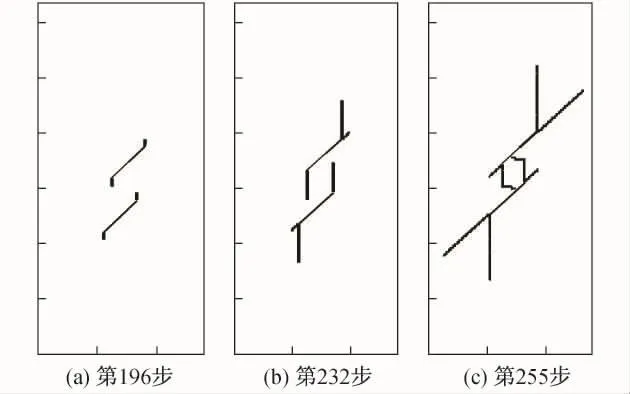
图10 β/α=45°/90°时不同荷载步下的裂纹扩展Fig.10 Fracture propagation at different loading steps when β/α=45°/90°
但从图11中也可以看出,数值模拟结果与试验结果存在一些差异.如在试验中试件会同时出现几条翼裂纹,而且有些是在裂纹中部开始扩展,而数值模拟结果中没有同时出现几条翼裂纹的情况,这主要是由于本模型中没有考虑岩石的非均质性问题.众所周知,岩石具有非均质特性,因而在受载过程中,裂纹会在薄弱点成核、扩展等,宏观上会出现随机裂纹现象.而在本模型中,岩石为均质材料,因而没有出现试验中的随机次生裂纹.但数值模拟结果能够基本再现裂纹扩展模式,与试验结果在整个趋势上是一致的.因而,应用包含摩尔-库仑准则的单元劈裂法可以模拟围压状态下的裂纹扩展和汇合行为.
4.3 不同围压下裂纹扩展对比分析
为分析不同围压下的裂纹扩展特点,本研究针对不同的岩桥倾角,分别施加0.35,0.70,1.50 MPa 3种不同围压对裂纹扩展进行模拟.图12为当β/α=45°/45°时,3种不同围压下的裂纹扩展模式.从图中可以看出,在围压由 0.35 MPa增大到0.70 MPa的过程中,裂纹扩展模式基本没有变化,只是在0.70 MPa围压下,张拉型翼裂纹扩展变“慢”了.但当围压增大到1.50 MPa时,张拉型翼裂纹不存在了,取而代之的是剪切型裂纹从内侧裂尖开始扩展.这是因为在低围压状态下,围压还不足以约束张拉型翼裂纹扩展;但随着围压逐渐增大,这种约束力越来越强,以至于张拉型翼裂纹扩展变“慢”;最后,随着围压的进一步增大,围压完全约束住了张拉型翼裂纹扩展,从而出现剪切裂纹扩展,这一趋势符合围压条件下的裂纹扩展特征.图13为当β/α= 45°/45°时,不同围压下的轴向应力-应变曲线.从图中可以看出,随着围压的增大,应力曲线的峰值也在增大,这与实际情况相符.
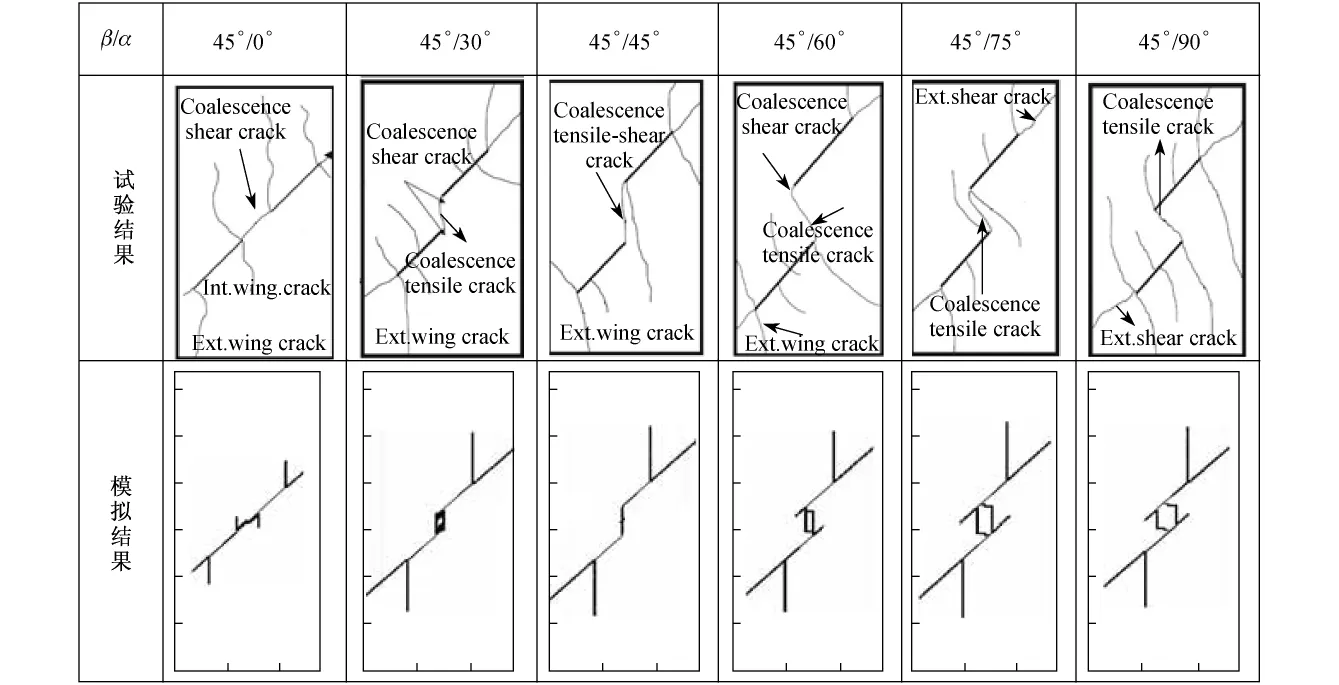
图11 裂纹汇合模式的试验结果[6]与模拟结果对比Fig.11 Comparison of the coalescence pattern between the experimental[6]and the simulated results
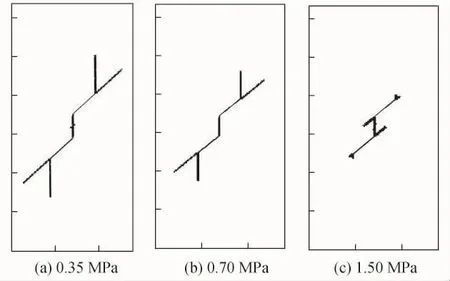
图12 不同围压下裂纹扩展对比(β/α=45°/45°)Fig.12 Comparison offracturepropagation under different confining stresses(β/α=45°/45°)
5 结束语
通过与现有双裂纹围压试验结果进行对比可以发现,包含摩尔-库仑准则的单元劈裂法可以较好地模拟出岩体节理的扩展和汇合过程,能基本再现岩体试件的破环特征.这是由于单元劈裂法能够在网格不变的情况下模拟节理的扩展和汇合行为,因此避免了重新划分网格,减少了计算量,从而在数值模拟节理岩体破坏的过程中具有一定的优势.但单元劈裂法没有考虑劈裂后所形成的2个块体自身的弹塑性变形,所以该方法只是一种近似方法.
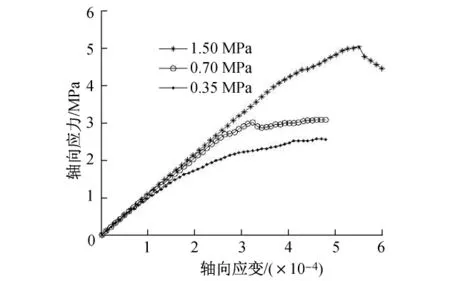
图13 不同围压下的轴向应力-应变曲线(β/α=45°/45°)Fig.13 Uniaxial stress-strain curves under different confining stresses(β/α=45°/45°)
[1] YANGS Q,DAIY H,HANL J,et al.Experimental study on mechanical behavior of brittle marble samples containing different flaws under uniaxial compression[J].Engineering Fracture Mechanics,2009,76:1833-1845.
[2] 栾茂田,张大林,杨庆,等.有限覆盖无单元法在裂纹扩展数值分析问题中的应用[J].岩土工程学报,2003,25(5):527-531.
[3] 车法星,黎立云,刘大安.类岩材料多裂纹体断裂破坏试验及有限元分析[J].岩石力学与工程学报,2000,19(3):295-298.
[4] 黄明利,冯夏庭,王水林.多裂纹在不同岩石介质中的扩展贯通机制分析[J].岩土力学,2002,23(2):142-146.
[5] GOODMANR E,TAYLORR L,BREKKET L.A model for the mechanics of joint rock[J].Journal of the Soil Mechanics and Foundations Division,1968,94:637-659.
[6] MUGHIEDAO,KARASNEHI.Coalescence of offset rock joints under biaxial loading[J].Geotechnical and Geological Engineering,2006,24:985-999.
[7] 张振南,陈永泉.一种模拟节理岩体破坏的新方法:单元劈裂法[J].岩土工程学报,2009,31(12):1858-1864.
[8] ZHANGZ N,CHEN Y Q.Simulation of fracture propagation subjected to compressive and shear stress field using virtual multidimensional internal bonds[J].International Journal of Rock Mechanics and Mining Sciences,2009,46(6):1010-1022.
[9] MOESN,DOLBOWJ,BELYTSCHKOT.A finite element method for crack growth without remeshing[J].Int J Numer Methods Engrg,1999,46(1):131-150.
[10] LARSSONR,FAGERSTROMM.A framework for fracture modelling based on the material forces concept with XFEM kinematics[J].Int J Numer Methods Engrg,2005,62(13):1763-1788.
