钢筋混凝土梁柱节点抗剪强度计算模型
2012-01-31陈玲俐
陈玲俐, 王 健
(上海大学土木工程系,上海200072)
钢筋混凝土梁柱节点作为框架结构中的重要一环,起着传递与分配结构内力的作用.历次震害表明,钢筋混凝土梁柱节点仍然是框架结构破坏的主要区域.从20世纪60年代开始,各国研究者针对钢筋混凝土梁柱节点的抗震性能进行了大量的试验与理论研究,但由于条件的限制,并未在节点核心区抗剪破坏理论方面达成一致.近几十年来,研究人员提出了各种不同的节点计算模型,试图解释节点的受力过程及破坏分化情况.这些模型可分为两类:微观模型与宏观模型.微观模型以钢筋混凝土有限元模型为代表,将节点核心区受力通过各种类型的刚性及弹簧单元来描述.按照模型发展过程来分,主要有以下几种[1]:转动铰模型、节点宏模型、超级节点单元模型和连续模型.微观模型具有大量的自由度和计算参数,计算量极为庞大,而且由于混凝土材料在复杂应力与加载路径下的本构关系不是很成熟,因此,微观模型在实际工程中的应用还不是很现实.宏观模型一般较为简单,力学概念简明,计算参数少,易于在工程实际中广泛应用.
宏观模型主要是在一些试验研究和理论简化假设的基础上提出的节点抗剪模型,其中比较有代表性的有Paulay等[2]提出的斜压杆-桁架模型、美国规范中所采用的压杆-拉杆模型[3]、Parra-Montesinos等[4]提出的等效斜压杆模型、傅剑平等[5]提出的梁柱简支杆模型、Hwang等[6]提出的三机构软化压杆-拉杆模型、Attaalla[7]提出的节点抗剪通用模型及Tsonos模型[8]等.这些模型大部分是在各自试验研究的基础上经过统计获得的经验公式,往往具有一定的局限性.Tsonos模型虽然受力机理清晰,但忽略了节点核心区开裂混凝土对抗剪的影响,并且对高强混凝土的分析存在极大偏差;软化压杆-拉杆模型将节点核心区受力简化为各个混凝土压杆的受力叠加,力学分析不明确;而Attaalla模型则基本抛弃了对节点受力机理的考量.因此,本研究对几种节点核心区抗剪强度宏观计算模型与多组节点试验进行了对比分析,并在原有节点抗剪强度计算公式基础上引入新的影响系数,提出了一种改进的简化计算方法.
1 几种宏观节点抗剪计算模型及比较分析
由文献[6-8]所进行的模型分析可知,美国规范、新西兰规范及日本规范对节点核心区抗剪强度的计算均基于各自的试验结果,具有明显的统计性.各规范利用传统的斜压杆模型和拉杆-压杆模型在计算节点核心区抗剪强度时的预测精度和离散度较差.本研究在目前3个比较有代表性的节点抗剪计算模型的基础上,利用收集的节点试验数据进行了模型比较分析.
1.1 Tsonos模型
1996年,Tsonos[8]在斜压杆-桁架机理基础上,引入混凝土的双轴本构关系,得到了节点核心区水平剪应力计算公式.Tsonos模型(见图1)中的节点核心区剪力主要由两部分承担:节点核心区斜向对角区域的混凝土斜压杆机构(见图1(b));节点核心区抗剪箍筋与竖向抗剪钢筋及开裂的受压混凝土形成的桁架机构(见图1(c)).由于这两种机构的承载能力均依赖于节点核心区混凝土强度,因此,节点核心区的抗剪承载能力由核心区混凝土在拉-压状态下的极限强度决定,即
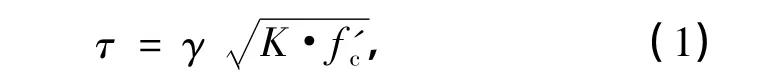
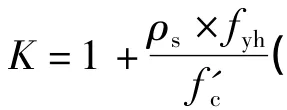
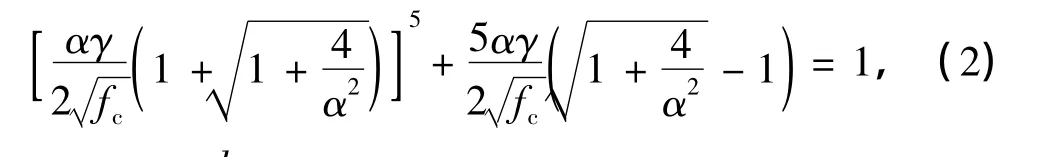
1.2 软化压杆-拉杆模型
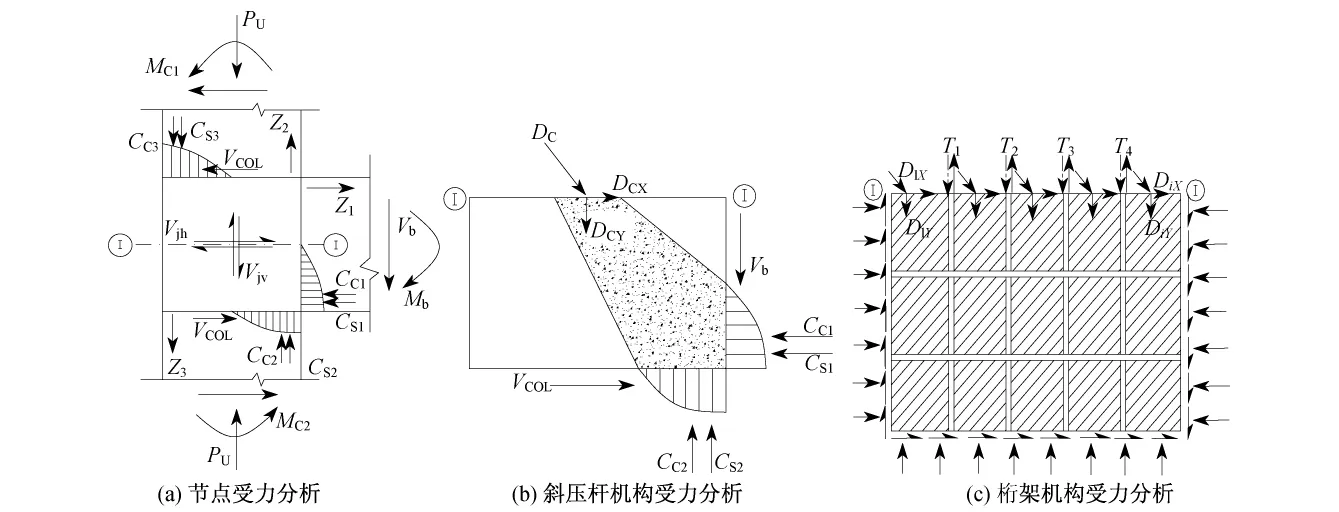
图1 Tsonos模型Fig.1 Tsonos model
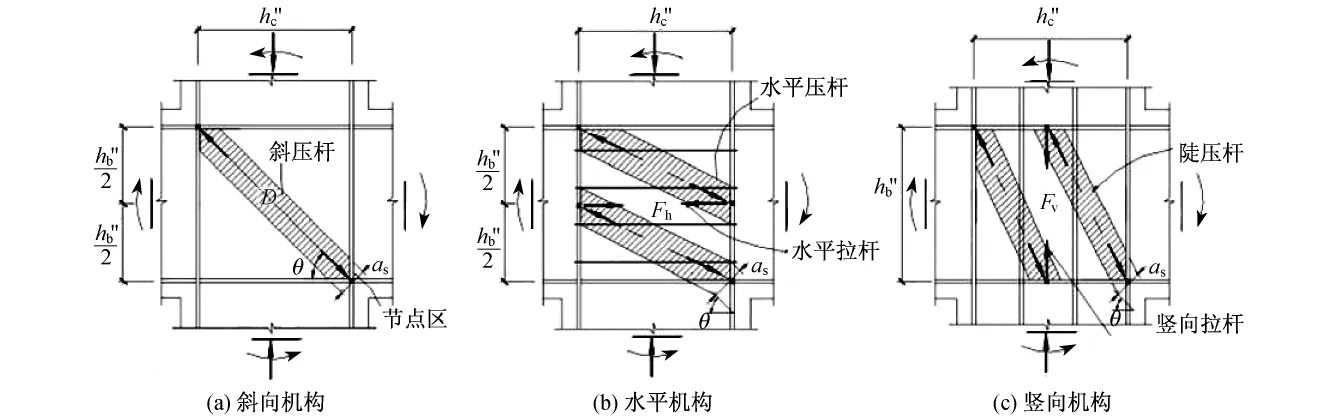
图2 软化压杆-拉杆模型Fig.2 Softened strut-and-tie model
1999年,Hwang等[6]在压杆-拉杆模型的基础上提出了考虑混凝土软化效应的软化压杆-拉杆模型(见图2).该模型满足节点核心区的静力平衡条件、莫尔协调条件和混凝土的软化双轴本构关系,由斜向机构(见图2(a))、水平机构(见图2(b))以及竖向机构(见图2(c))组成.斜向机构是一个斜向压杆,由节点核心对角的混凝土形成;水平机构包括1个水平拉杆和2个水平压杆,水平拉杆由节点箍筋形成,水平压杆由斜向混凝土形成;竖向机构包括1个竖向拉杆和2个陡压杆,竖向拉杆由柱中部钢筋组成,陡压杆由斜向受压混凝土形成.
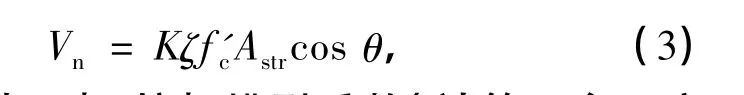
1.3 Attaalla模型
2004年,Attaalla等[7]为了解决因节点核心区抗剪理论的不统一而造成的节点核心区抗剪强度计算公式不一致的问题,提出了可以估计抗震区梁柱节点核心区抗剪强度的通用分析模型.该分析模型假定节点核心区内的应力应变是均布的,根据钢筋混凝土梁柱节点隔离体的平衡条件,并且考虑混凝土开裂的影响和对高强混凝土的修正,节点抗剪强度通用计算公式如下:
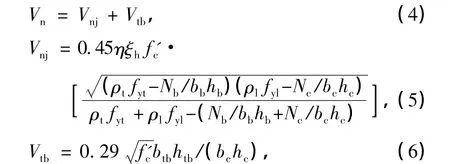
式中,η为节点的类型系数,内节点取1.0,外节点取0.79;ξh为高强混凝土的修正系数;ρt和ρl分别为节点水平和竖直方向的配筋率;fyt和fyl分别为节点水平和竖直方向钢筋的屈服强度;Nb和Nc分别为梁和柱的轴力;bb和hb分别为梁的宽度和高度; bc和hc分别为柱的宽度和高度;btb和htb分别为直交梁的宽度和高度.
1.4 模型比较及分析
理论上,Tsonos模型的受力机理很清晰;软化压杆-拉杆模型在表面上看似乎受力机理清晰,但是其将核心混凝土应力描述为斜压杆、水平压杆和陡压杆的压应力之和,这在力学原理上无法成立; Attaalla模型则基本抛弃了对节点受力机理的考量.为了进一步评价3个模型的优劣,本研究收集了国内外关于节点试验的8组共40个构件的实测数据[8,10-16]进行比较分析(见图3),理论值与试验值比值的统计结果如表1所示.
从图3及表1中可以看出,对于普通混凝土节点,Attaalla模型、软化压杆-拉杆模型及Tsonos模型的计算结果离散度较大.对于高强混凝土,Attaalla模型、软化压杆-拉杆模型的计算结果吻合度相对较好;Tsonos模型的理论计算值与试验值之比的平均值为1.93,计算值明显偏大,这说明Tsonos模型不适用于高强混凝土节点抗剪强度的计算.
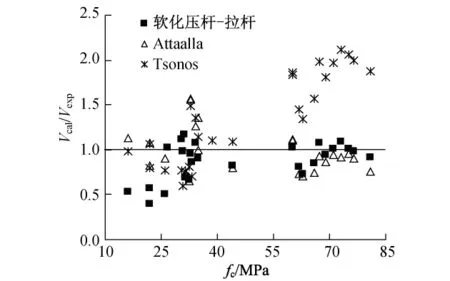
图3 理论计算值与试验值比值Fig.3 Ratio of theory vs.experience
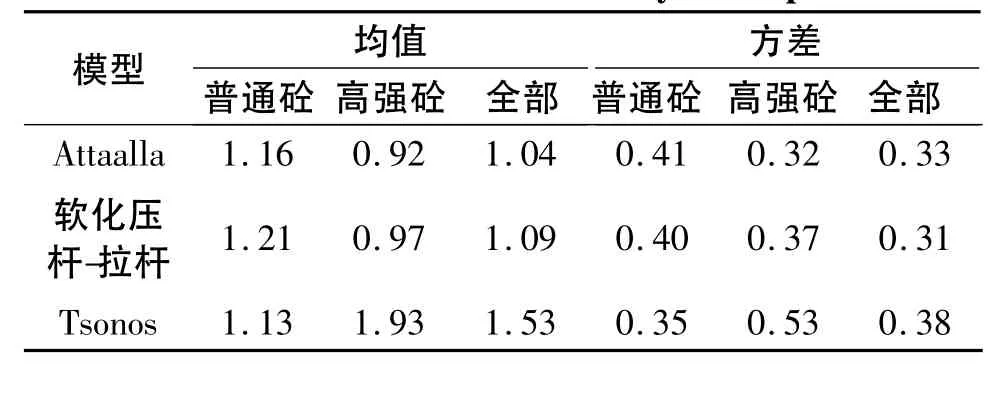
表1 节点理论值/试验值的统计结果Table 1 Statistics of ratio of theory vs.experience
2 改进模型及分析
由于Tsonos模型的受力机理清晰,因此,本研究通过对Tsonos模型未考虑的一些影响因素进行补充,得到了改进的节点抗剪强度计算模型.补充考虑的因素主要包括开裂混凝土的受压软化效应、高强混凝土及节点类型(周边约束情况)对节点抗剪强度的影响.
首先,通过对上述3种模型的分析过程进行比较后发现,软化压杆-拉杆模型及Attaalla模型均考虑了开裂混凝土软化效应对节点抗剪强度的影响,但在Tsonos模型中,并未对此加以考虑,因此,在Tsonos模型基础上,本研究增加了开裂混凝土受压软化影响系数.
其次,高强混凝土与普通混凝土相比不仅仅是其混凝土抗压强度明显提高,其本构曲线的形态也有较明显的变化,因此,如果在高强混凝土节点抗剪强度分析中沿用普通混凝土节点的抗剪分析模型,就需要对节点抗剪强度进行必要的修正.已有研究表明,随着混凝土节点强度的提高,节点抗剪强度增速变缓[17].对此,本研究借鉴Attaalla模型的处理方法,在节点抗剪分析模型中引入一个节点抗剪强度比修正系数ξh,用以反映混凝土抗压强度与节点抗剪强度的非线性变化关系.
2.1 开裂混凝土软化效应
目前,研究者对开裂混凝土受压软化影响系数的计算方法还有较大争议,如表2[13,18]所示,表中ε1为第一主应变,ε2为第二主应变,ε0为混凝土峰值应变.

表2 开裂混凝土软化系数Table 2 Cracked concrete softening coefficient
以上对于节点核心区抗剪强度的计算仅仅涉及到混凝土的极限抗压强度,因此,本研究对表2中的建议公式进行了比较分析.从峰值软化系数来看,峰值应力处软化系数ζ大致可分为两类:一类集中在0.8附近,另一类则集中在0.6附近.本研究在综合前人研究的基础上发现,当受压作为主控条件进行钢筋混凝土平板试验时,受压软化系数取值偏大[18].据此,本研究建议节点核心区ζ取0.85.加入开裂混凝土受压软化影响系数后,Tsonos模型可以表述为
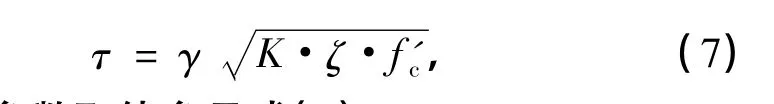
式中,其他参数取值参见式(1).
将改进计算后的理论值与试验值的比值与原有的计算结果相比较可以发现,理论值与试验值的差值缩小,波动降低(见表3).而高强混凝土经过改进计算后的理论值与试验值比值的均值与方差分别为1.23和0.17,虽然波动已经降低,但计算结果仍然偏大.
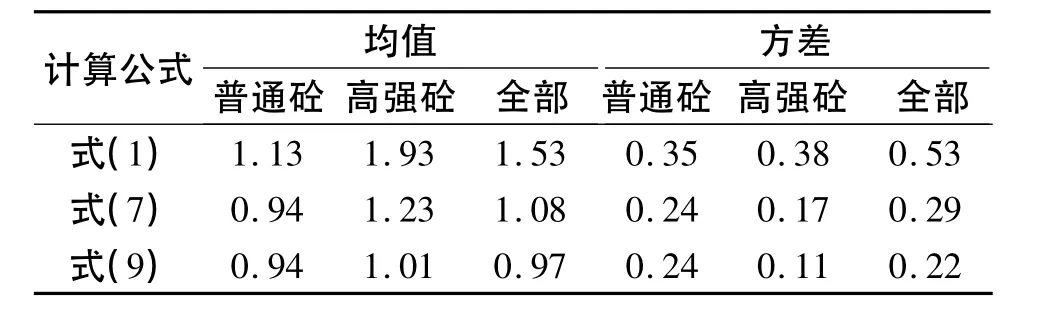
表3 改进计算统计表Table 3 Statistics of modified calculation
2.2 高强混凝土调整系数
对于高强混凝土节点,在对所采用试验节点数据进行多组拟合分析后可以发现,乘幂曲线拟合使计算结果与试验结果的拟合度最高,因此,本研究在式(7)的基础上引入高强混凝土调整系数ξh:
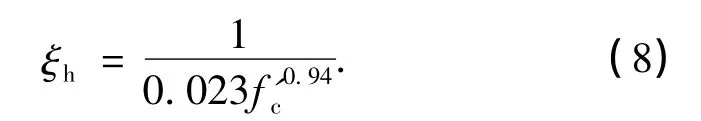
综合以上因素,得到改进的节点抗剪模型对节点核心区抗剪强度的计算公式如下:
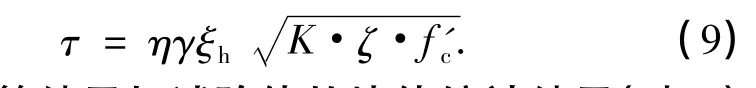
式(9)的计算结果与试验值的比值统计结果(表3)表明,无论是普通混凝土还是高强混凝土,改进模型理论计算值与试验值都非常接近,离散度降低.
3 结论
通过对 Tsonos模型、软化压杆-拉杆模型和Attaalla模型的分析过程进行比较,本研究主要针对Tsonos模型开展了节点抗剪强度计算模型的评价与修正,得到如下结论.
(1)通过试验评价不同模型的计算结果发现,对于普通混凝土节点,Tsonos模型、软化压杆-拉杆模型及Attaalla模型的计算结果偏大13% ~21%,且离散度较大.对于高强混凝土,Tsonos模型理论计算值与试验值偏差过大,Attaalla模型、软化压杆-拉杆模型的吻合度相对较好.
(2)在改进的节点抗剪计算模型中考虑开裂混凝土软化效应后,整体计算结果的离散度降低;对于普通混凝土,计算结果较试验结果小6%,偏于安全;对于高强混凝土,计算结果仍然略为偏大.
(3)通过试验拟合,本研究给出了高强混凝土抗剪强度调整系数计算公式.采用该公式计算得到的高强混凝土节点的抗剪强度计算结果不仅与试验结果相吻合,且方差明显降低,适于工程实际应用.
[1] 吴健秋.基于OpenSees的梁-柱节点单元的适用性和定参方法研究[D].重庆:重庆大学,2007:1-4.
[2] PAULAYT,PARKR,PRIESTLEYM J N.Reinforced concrete beam-column joints under seismic actions[J].ACI Structural Journal,1978,75(11):585-593.
[3] ACICommittee 318.Building code requirements for structural concrete(ACI 318-02)[M].Farmington Hills,MI:ACI,2008.
[4] PARRA-MONTESIONSG J,WIGHTJ K.Prediction of strength and shear distortion in R/C beam column joints[C]∥Uzumeri Symposium:Behavior and Design of Concrete Structure for Seismic Performance.2002:191-204.
[5] 傅剑平,张川,白绍良.钢筋混凝土抗震框架节点各机构传递剪力的定量分析[J].建筑结构学报,2005,26 (1):91-96.
[6] HWANGS J,LEEH J.Analytical model for predicting shear strengths of interior reinforced concrete beamcolumn joints for seismic resistance[J].ACI Structural Journal,2000,97(4):35-44.
[7] ATTAALLAS A.General analytical model for nominal shear stress of type 2 normal-and high-strength concrete beam-column joints[J].ACI Structural Journal,2004,101(1):65-75.
[8] TSONOSA G.Cyclic load behavior of reinforced concrete beam-column sub assemblages of modern structures[J].ACI Structural Journal,2007,104(4):468-478.
[9] ZHANGL,JIRSAJ O.A study of shear behavior of reinforced concrete beam-column joints[R].PMFSEL Report No.82-1.Austin:University of Texas,1982.
[10] 李宏仁.钢筋混凝土抗震梁柱节点抗剪强度研究[D].台北:台湾科技大学,2002:45-53.
[11] HWANGS J,LEEH J.Role of hoops on shear strength of reinforced concretes beam-column joints[J].ACI Structural Journal,2005,102(3):445-453.
[12] TSONOSA G.Effectiveness of CFRP-jackets and RC-jackets inpost-earthquake and pre-earthquake retrofitting of beam column subassemblages[J].Engineering Structures,2008,30(9):777-793.
[13] 叶欲凡.钢筋混凝土梁柱节点剪力衰减模型应用于框架层间剪力与变形的预测[D].桃源:中央大学,2001:76-91.
[14] KITAYAMAK,OTANIS,AOYAMAH.Earthquake resistant design criteria for reinforced concrete interior beam-column joints[C]∥ PacificConferenceon Earthquake Engineering.1987:315-326.
[15] 朱春明,王溥,陈敬安.钢筋混凝土框架节点的抗剪强度[C]∥ 第二届混凝土结构基本理论及应用讨论会.北京:清华大学出版社,1990:485-492.
[16] ATTAALLAS A,AGBABIANM S.Performance of interiorbeam-column joints castfrom high strength concrete underseismic loads[J]. Advances in Structural Engineering,2004,7(2):147-157.
[17] EHSANIM R,ALAMEDDINEF.Design recommendations for type 2 high-strength reinforced concrete connections[J].ACI Structural Journal,1991,88(3):277-291.
[18] 武守信.开裂钢筋混凝土本构模型研究[D].成都:西南交通大学,1996:15-95.
