基于Chebyshev多项式逼近的分数阶微积分数值算法
2012-01-31李常品
陈 安, 李常品
(上海大学理学院,上海200444)
分数阶微积分拥有长达300多年的历史,但直到近几十年才得到快速发展[1].这主要是因为分数阶能够比整数阶更好地刻画现实中的复杂模型,尤其是对一些具有记忆与遗传性质的物质的刻画[2].不过也正因为分数阶微分的非局部性,导致了其数值计算的困难.Diethelm等[3]总结了关于分数阶微积分的几种常见的数值算法,本质上是利用函数的线性插值来构造相应的数值公式.Yuan等[4]构造了一种新的数值格式,这种格式能有效地避免因分数阶微分的非局部性而引起的高计算复杂度.之后,Diethelm[5]对该格式进行了改进,改进方法的主要思想是把原问题转化为更易求解的积分问题,然后利用 Gauss公式求解.为了得到更高阶的算法,Miyakoda等[6-8]基于Chebyshev多项式建立了一种新数值格式,然而,他们仅讨论了分数阶微分(t)在0<α<1时的情况.Li等[9]基于插值函?数,对分数阶微积分提出了几种新的有效数值算法.关于分数阶偏微分方程的有限元方法可参见文献[10-12],其中文献[11]是关于分数阶偏微分方程间断有限元方法的早期工作,文献[12]是关于分数阶超扩散问题有限元方法的早期工作.
本工作基于Chebyshev多项式逼近建立了高阶的分数阶积分与Caputo型分数阶导数的数值算法,推广了文献[6-8]中α的应用范围.
下面,首先给出2个相关的基本定义.
定义1 关于函数 f(t)分数阶积分的定义如下:
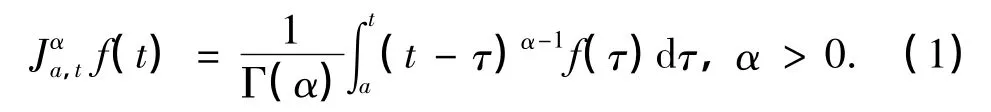
定义2 关于函数f(t)的Caputo型分数阶导数的定义如下:
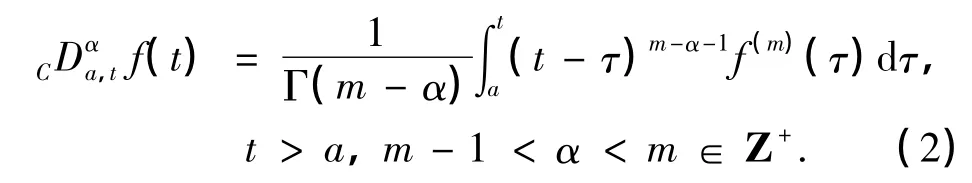
1 分数阶微积分数值算法的建立
为了简便起见,对式(1)和(2)仅考虑a=0及0≤t≤1时的情况,其中对式(2)只讨论m=2时的情况(m=1时的情况可参见文献[7-8]).
1.1 分数阶积分数值算法
利用移位Chebyshev多项式Tk(2t-1)对式(1)中的f(t)进行逼近[7-8],有
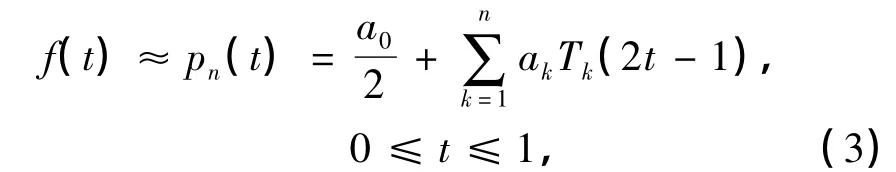
式中,
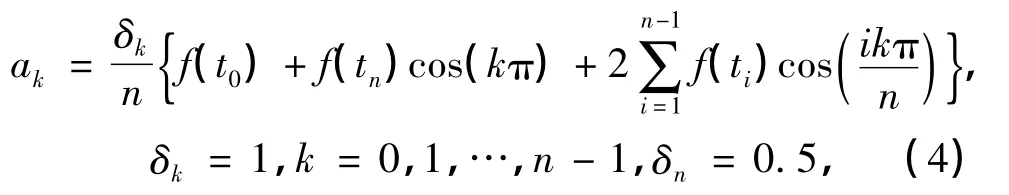
其中插值节点为
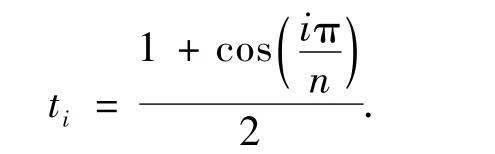
Chebyshev多项式 Tk(x)可用如下递归公式得到:
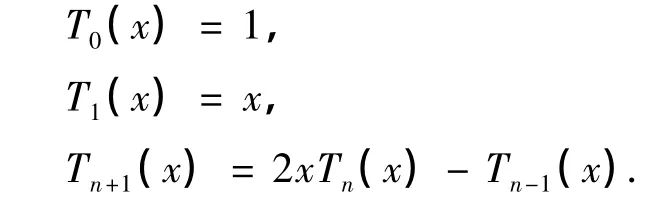
将式(3)代入式(1),有
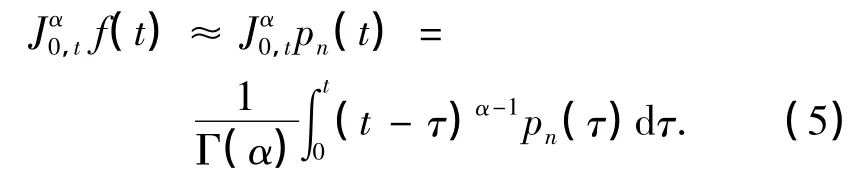
为了得到式(5)的具体表示,给出下面的引理.
引理1 记pn为式(3)的n次多项式,则存在相应的阶数为n的多项式Ln,满足
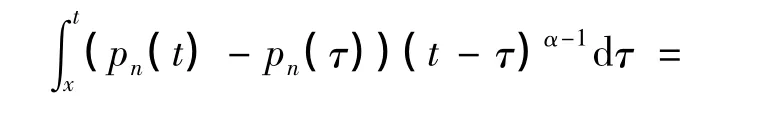
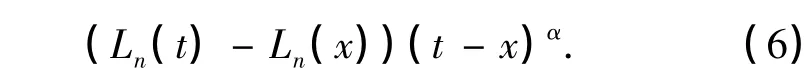
证明 对pn(τ)在t处Taylor展开,有
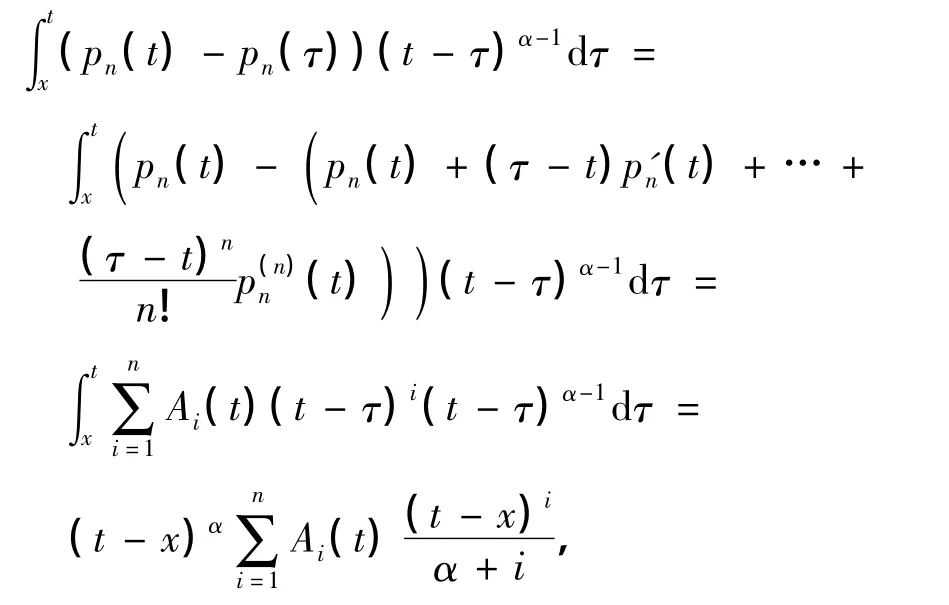
首先,在引理1中取x=0并对其化简,得到
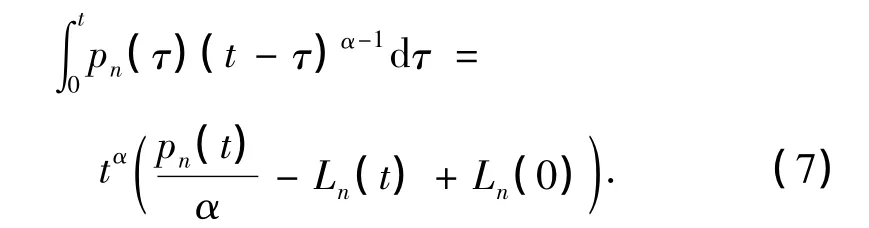
然后,式(6)两边同时对x求导,整理,有
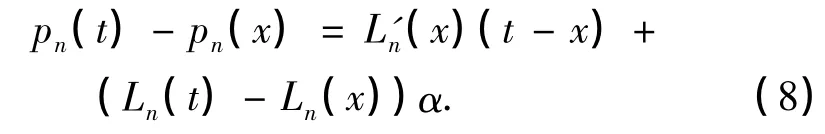
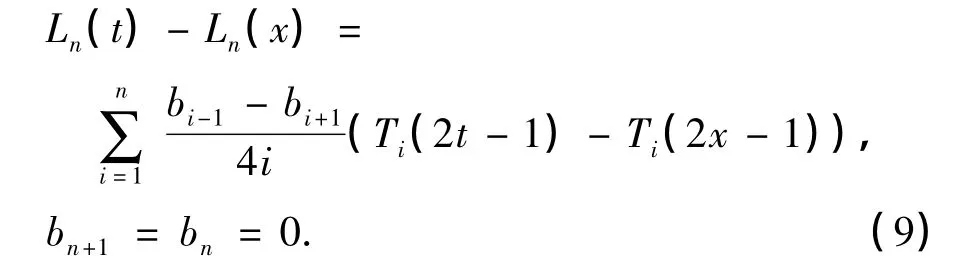
由式(7)可知
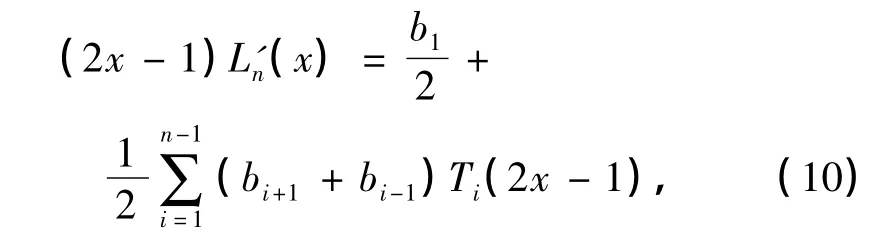
从而
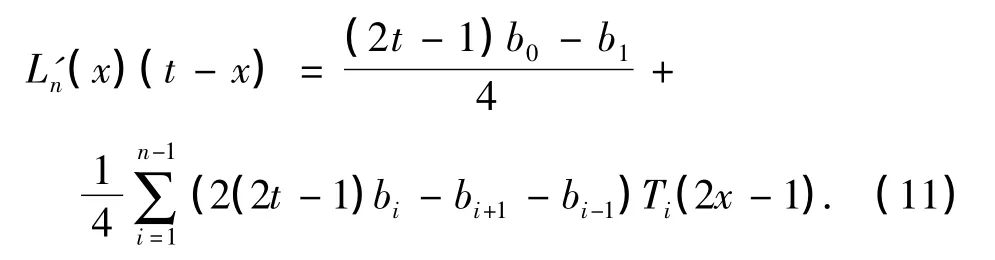
将式(3),(9)及(11)代入式(8),得
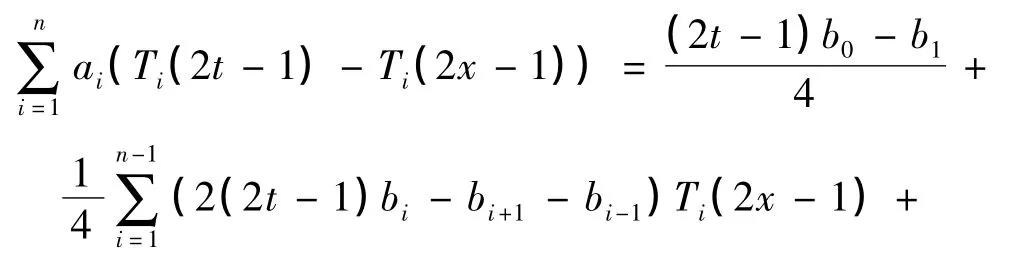
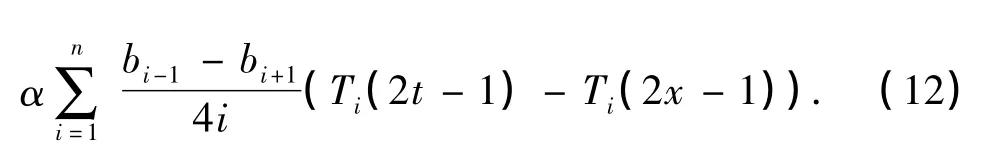
注意到,只需知道式(9)中bi的值便可以推导出分数阶积分的数值表达式,因此,对比式(12)中左右两边Ti(2x-1)(i=1,2,…,n)前的系数,并整理,得到
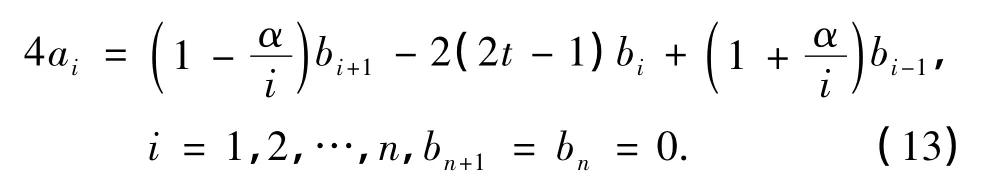
综上,可得到关于分数阶积分(1)的数值算法如下:
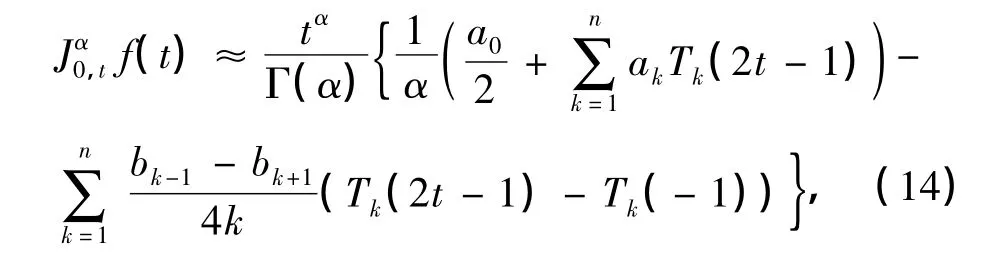
式中,α>0,t∈[0,1],而ak及bk可分别由式(4)和(13)得到.
1.2 Caputo型分数阶导数的数值算法
下面主要讨论式(2)中1<α<2时的情况,对于0<α<1时的情况可参见文献[7].
类似于分数阶积分数值算法的讨论,仍利用移位Chebyshev多项式对f(t)进行逼近
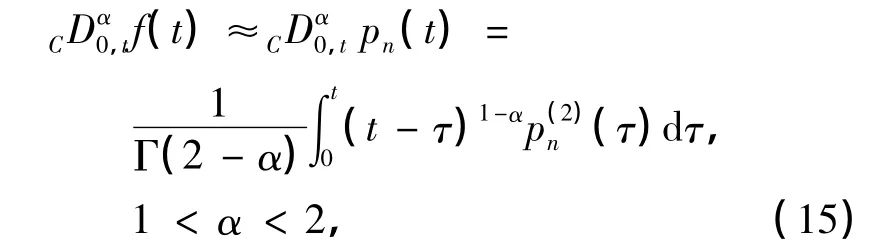
式中,pn可由式(3)得到.下面给出一个引理,其证明过程类似引理1,这里不再赘述.
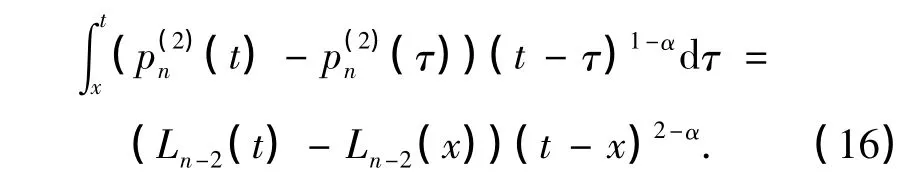
令x=0,并化简,得
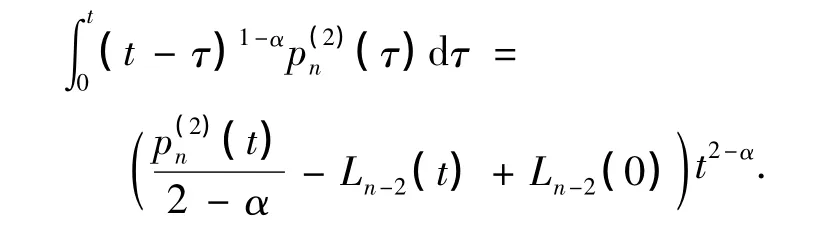
因此,由式(15)可以进一步得到
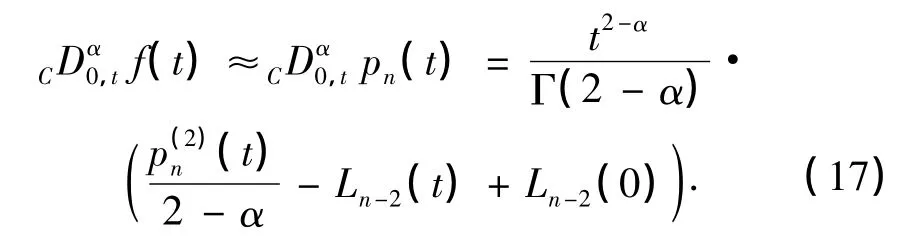
为了得到式(17)右端的具体表示,首先在式(16)两边同时对x求导,整理后,得
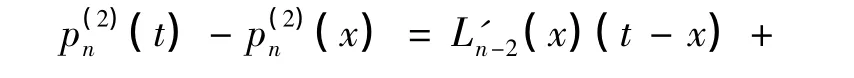
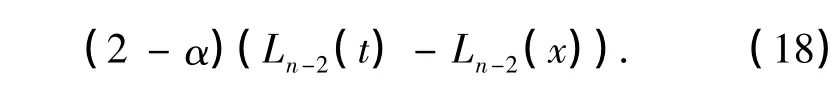
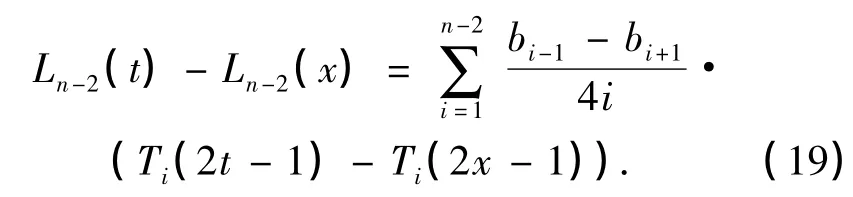
然后,结合式(10),有
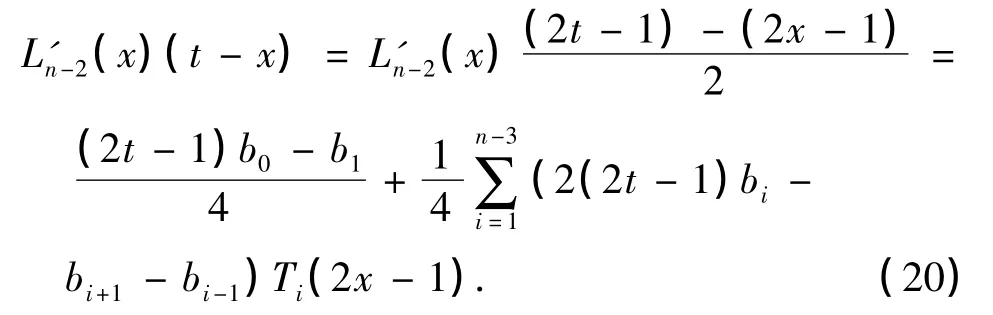
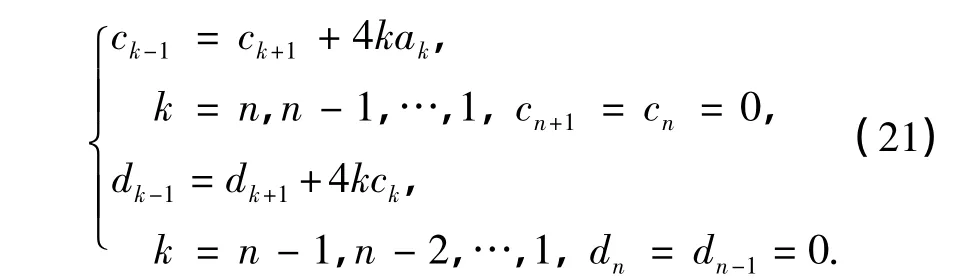
为了确定式(19)中的bi,把式(19)和(20)代入式(18),并整理,得
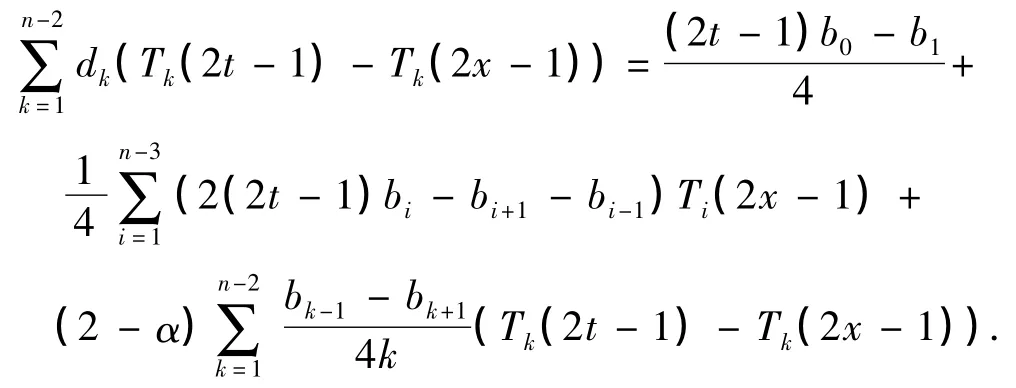
由于只需知道式(19)中的bi,i=1,2,…,n-2,则对比上式两边Tk(2x-1)前的系数,整理,于是得到
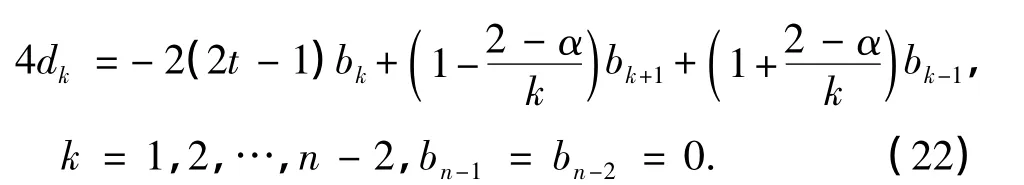
综上,得到Caputo型的分数阶导数的数值算法如下:
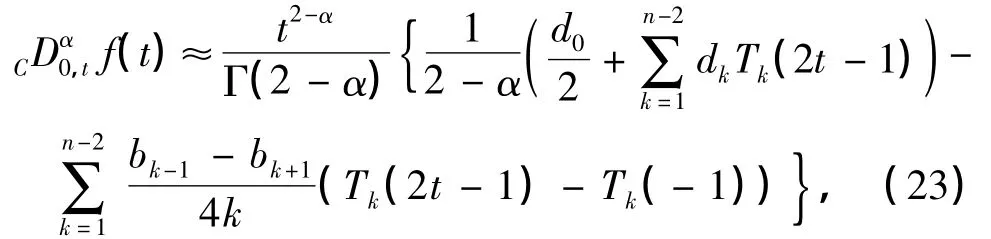
式中,α∈(1,2),t∈[0,1],而dk,bk分别由式(21)和(22)决定.
我们在建立数值算法(式(23))时发现,对于α可进一步推广至α>2时的情况,这里不再重述其推导过程.
2 误差分析
下面依次给出式(5)和(15)的误差分析.由文献[7,13]可以得到

下面给出式(5)的一致有界性,即其与t在区间[0,1]的取值无关.
引理3 基于Chebyshev多项式pn(t)逼近的分数阶积分的数值算法是一致有界的,即
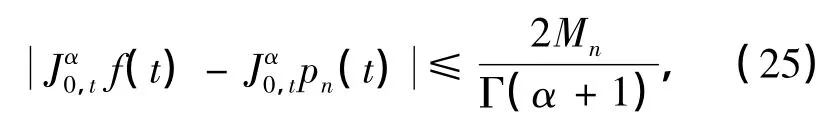
式中,
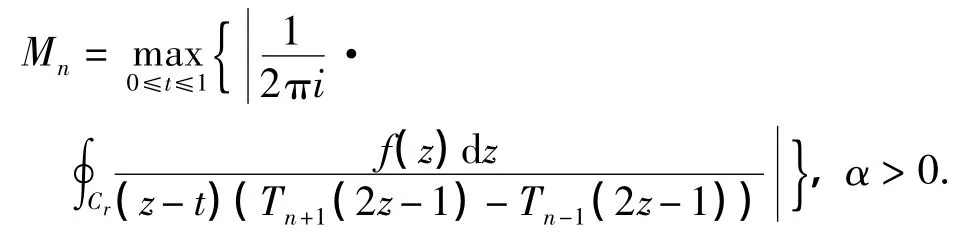
证明 注意到,|Tn+1(2t-1)-Tn-1(2t-1)|≤2,故|f(t)-pn(t)|≤2Mn,从而结合式(5),有
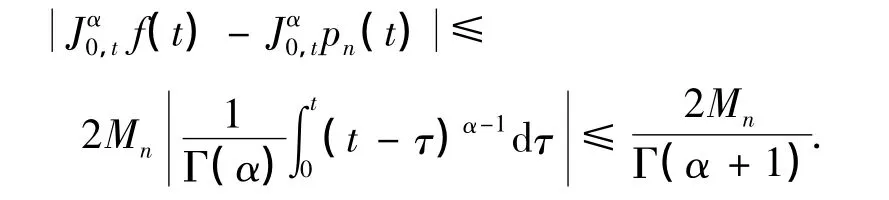
定理1 假设 f(z)在 Cr上解析,则基于Chebyshev多项式pn(t)逼近的分数阶积分的数值算法有如下误差估计:
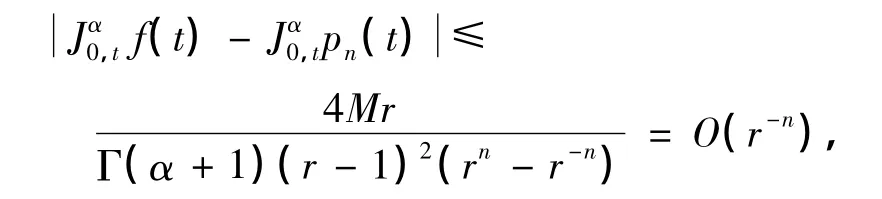
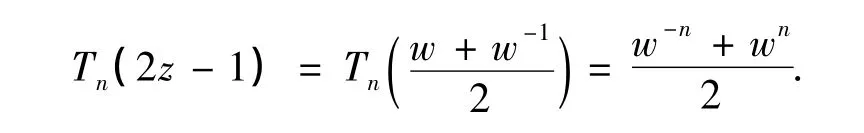
结合引理3,有
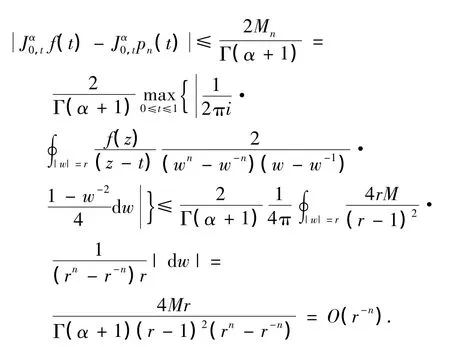
最后,给出式(15)的误差估计.为了讨论的方便,记
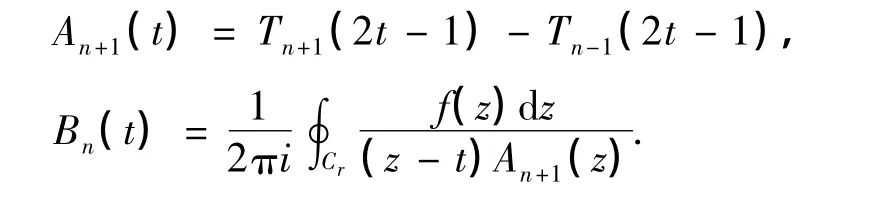
这样,式(24)可写成

下面给出一个引理.
引理4 基于Chebyshev多项式pn(t)逼近的Caputo型分数阶导数的数值算法是一致有界的,即
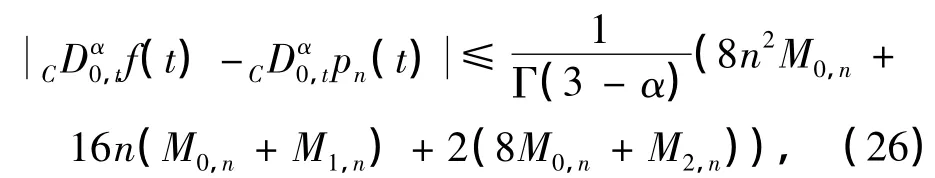
式中,

证明 由于E″n(t)=A″n+1(t)Bn(t)+2A'n+1(t)· B'n(t)+An+1B″n(t),另外,根据Chebyshev多项式的相关性质,可以得到如下估计:
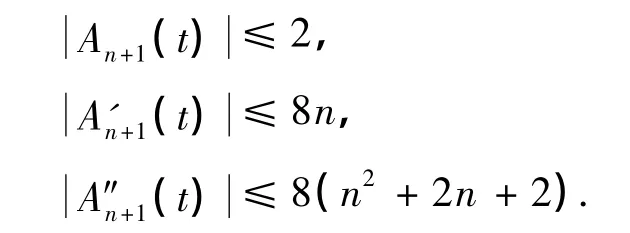
因此,
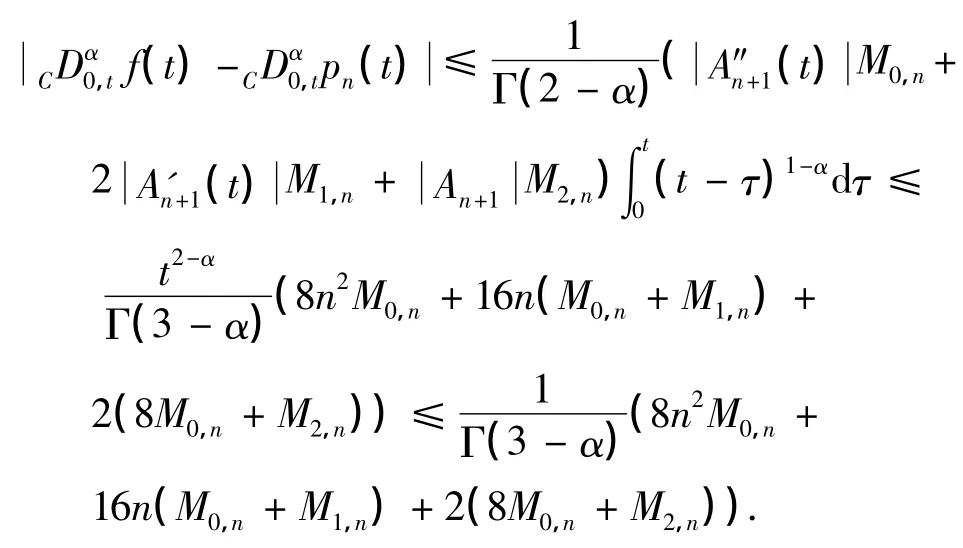
定理2 假设f(z)在Cr上解析,则基于Chebyshev多项式pn(t)逼近的Caputo型分数阶导数的数值算法有如下误差估计:
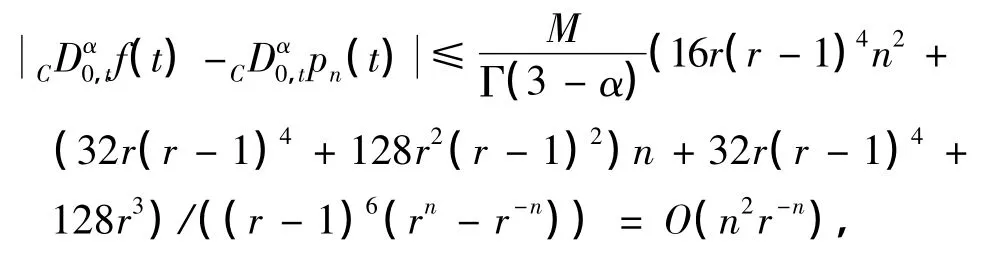
证明 由定理1的证明过程易得
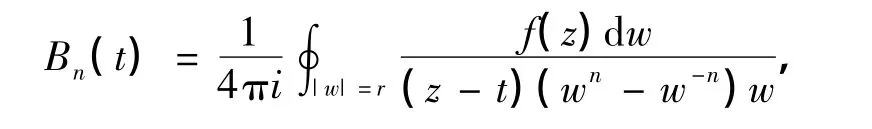
且

从而有
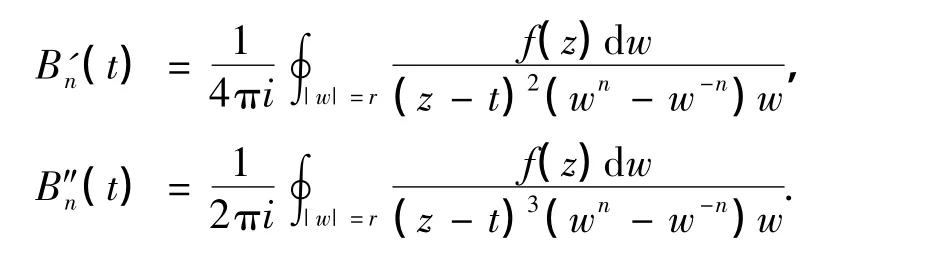
对上式进行估计,有
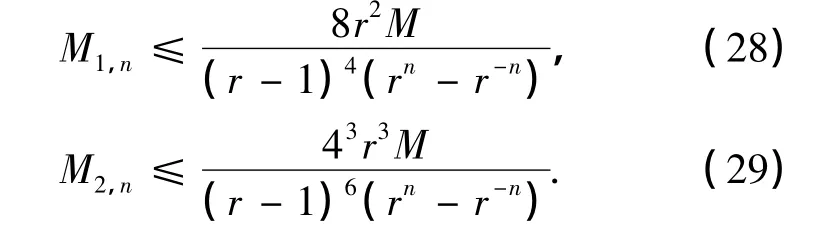
因此,把式(27)~(29)代入引理4中的式(26),整理,即可证明.
定理1及定理2中的“O”表示当n趋向无穷大时,数值算法误差的收敛速度的快慢.容易看出,本工作提出的基于Chebyshev多项式逼近建立的分数阶积分数值算法(式(14))及Caputo型分数阶导数数值算法(式(23))具有较快的收敛速度.
3 数值算例
设f(t)=tβ,则
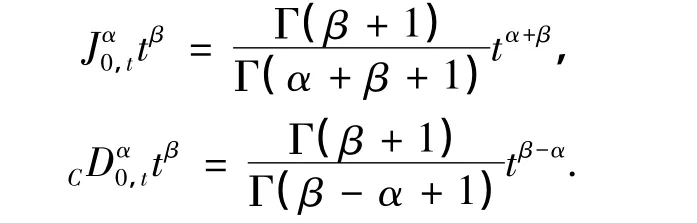
在式(14)中取β=4,在式(23)中取β=5,则可分别得到对应的n的分数阶积分及Caputo型分数阶导数的数值解,同时,将它们与文献[3]中的线性插值方法相比较.
从表1和表2中的误差结果可以发现,对本算例而言,在分数阶积分的数值格式中,n=4时的收敛速度要比n=2时好得多;而在分数阶微分的数值格式中,n=8时的收敛速度要比n=4时好得多.对于其他情况,则可根据相应的f(t)来变动n值.此外,通过对比2种不同的计算方法的数值结果可知,本工作建立的分数阶积分及Caputo型分数阶导数的数值算法,即式(14)与(23),它们的收敛速度均高于文献[3]中所提及的线性插值方法,且推广了文献[7]中的数值方法.
表1 的绝对误差Table 1 Absolute error of

表1 的绝对误差Table 1 Absolute error of
α绝对误差线性插值法[3]Chebyshev多项式逼近法(式(14 =4 0.2 6.810 969E-002 2.226 088E-002 2.652 089E-n=2 n=4 )) n=2 n 002 3.330 669E-016 0.6 1.013 351E-001 2.868 810E-002 2.709 820E-002 2.220 446E-016 1.4 5.349 327E-002 1.272 141E-002 5.929 401E-003 1.249 001E-016 1.8 3.183 041E-002 7.270 493E-003 1.188 870E-002 2.081 668E-017
表2 的绝对误差Table 2 Absolute error of

表2 的绝对误差Table 2 Absolute error of
α绝对误差线性插值法[3]Chebyshev多项式逼近法(式(23 =8 1.2 3.600 270E-001 9.147 084E-002 7.433 626E-n=4 n=8 )) n=4 n 002 8.881 784E-016 1.4 3.912 311E-001 1.020 049E-001 2.053 614E-001 1.065 814E-014 1.6 3.802 527E-001 1.030 250E-001 4.273 832E-001 1.065 814E-014 1.8 2.787 430E-001 7.964 166E-002 7.920 905E-001 2.486 900E-014
[1] PODLUBNYI.Fractional differential equations[M].San Diego,CA:Academic Press,1999:261-307.
[2] 徐明瑜,谭文长.中间过程、临界现象——分数阶算子理论、方法、进展及其在现代力学中的应用[J].中国科学:G辑,2006,36(3):225-238.
[3] DIETHELMK,FORDN J,FREEDA D,etal.Algorithms for the fractional calculus:a selection of numerical methods[J].Comput Methods Appl Mech Eng,2005,194:743-773.
[4] YUANL,AGRAWALO P.A numerical scheme for dynamic systems containing fractional derivatives[J].ASME J Vibr Acoust,2002,124:321-324.
[5] DIETHELM K.An improvementofanonclassical numerical method forthe computation offractional derivatives[J].Numer Algor,2009,131(1):014502-4.
[6] MIYAKODAT.Discretized fractional calculus with a series of Chebyshev polynomial[J].Electronic Notes Theor Comput Sci,2009,225:239-244.
[7] SUGIURAH,HASEGAWAT.Quadrature rule for Abel’s equations:uniformly approximating fractional derivatives[J].J Comput Appl Math,2009,223:459-468.
[8] HASEGAWAT,SUGIURAH.Uniform approximation to fractional derivatives of functions of algebraic singularity[J].J Comput Appl Math,2009,228:247-253.
[9] LIC P,CHENA,YEJ J.Numerical approaches to fractional calculus and fractional ordinary differential equation[J].J Comput Phys,2011,230(9):3352-3368.
[10] ZHENGY Y,LIC P,ZHAOZ G.A note on the finite elementmethod for the space-fractional advection diffusion equation[J].Comput Math Appl,2010,59 (5):1718-1726.
[11] ZHENGY Y,LIC P,ZHAOZ G.A fully discrete discontinuous Galerkin method for nonlinear fractional Fokker-Planck equation[J].Mathematical Problems in Engineering,2010,doi:10.1155/2010/279038.
[12] LIC P,ZHAOZ G.Numerical approximation of nonlinear fractional differential equations with subdiffusion and superdiffusion[J].Comput Math Appl,2011,62(3):855-875.
[13] ELLIOTTD.Truncation errors in two Chebyshev series approximations[J].Math Comput,1965,19:234-248.
