基于2DPCA的颅骨识别研究

熊泽本

(荆楚理工学院数理学院，湖北荆门 448000)

生物特征识别技术主要是通过辨别人类的生理特征如手形、指纹、脸形、虹膜、视网膜等，或者是行为特征如字迹、声音等进行身份鉴别认证技术.其特征识别技术主要涉及到计算机视觉技术、图像和语音处理技术、可视化模拟、传感器和智能机器人探测系统等.颅骨在人体的内部，特征稳定，并且不易被破坏，所以它不易伪装，相对于指纹和人脸识别系统来说，有更高的稳定性，而且每个人的颅骨特征也不相同，至今为止，还没有发现两个人有完全相同的颅骨，而且只要人成年后，颅骨特征一般就不会发生改变了，基于颅骨特征的众多优点，基于颅骨的生物特征识别技术是当前国内外学者研究的热点.

1 特征信息获取与识别

在进行颅骨特征识别前，先要对医学扫描图像进行预处理，包括要对图像进行除噪、插值、分割处理，预处理完成后就要对图像进行三维重建，在这里采用的是基于等值面提取的表面重建算法，获得颅骨的三维模型，文中获取的是颅骨的三维网格信息，利用的是Marching Cubes算法，在VC软件开发平台上编程实现，三维网格信息中既包括颅骨的三维几何信息，同时还有三维模型的网络拓扑信息，基于本文的目的就是想对颅骨的几何信息进行研究，所以又对得到的三维信息进行处理，利用Matlab编程提取出颅骨的三维几何信息，获取信息后就要进行识别的关键处理，也即物体的特征提取.

2 三维网格模型几何数据获取

三维模型数据压缩算法有很多种，根据三维模型的表达式，一般都用网格结构对它进行描述，一个三维网格模型是由几何数据、拓扑数据和属性数据组成的［1］.有的时候图像中可能没有属性数据，只有几何和属性数据两种.几何数据，它描述的是顶点的位置坐标.拓扑数据描述的是面与面、顶点与顶点的一种连接关系，属性数据描述的是各个顶点的颜色值和它的纹理特征.文中是想通过颅骨的坐标值来对其进行识别，所以在对图像模型进行处理时，只是针对图像的几何数据进行压缩，因为它描述的是顶点的坐标值.

首先利用MATLAB编程PLY格式的数据转换为三维网格数据.编程代码为:

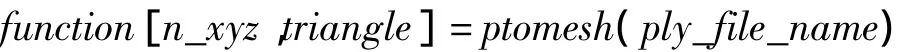
然后再利用编程把三维网格中的几何坐标提取出来

这样就把三维网格模型的几何数据读取了出来，也就是把模型的顶点坐标读取了出来，接下来的目的就是要对这些坐标值进行压缩处理，进而选取出重要的特征点进行识别.实际上就涉及到一个多行三列的矩阵问题.进而就把问题转化到了二维空间，这时所得的数据量就相当于一幅二维的图像.接下来就要利用模式识别的知识对图像数据进行处理，提取里面的重要特征.实验结果如下图1所示:

图1 颅骨重建

3 特征识别方法概述

在收集信息的过程中，总是希望能够从众多信息中把我们感兴趣的那部分信息提取出来.这样在进行模型识别时就可以提高速度，节省时间.而且维数大的模式空间在处理时可能会导致系统瘫痪，还有就是维数太多也会影响数据的分类.而且并不是每一个特征对事物的描述都有相同意义.特征选择和提取的基本任务就是如何从许多特征中找出那些最有效的特征.把特征提取出来后，目的就是为了后边的分类识别使用.在对物体进行分类识别时，必须使提取出特征的错误概率最小.

在对图像进行处理时，用到的特征一般有［2］:

(1)直观性特征.不用经过处理，一看就知道的特征，这种也是最简单的特征识别.它包括图像的边缘、纹理、几何形状等等，直观性特征具有速度快，识别率高的特点.

(2)统计特征，如直方图特征，主分量特征等，将图像看作一种二维随机过程，可以引入统计上的各阶矩作为特征来描述和分析图像，它们能够在保留主要分类信息的基础上大大降低特征的维数.

(3)变换系数特征，对图像进行各种数学变换，可以将变换的系数作为图像的一种特征，如Fourier变换、极半径均差Legender变换等在图像特征提取中均有广泛的应用.

特征提取的步骤可以分为特征形成和特征提取.特征形成就是被识别对象所产生的一组基本特征，它可以是计算出来的，也可以是用传感器，智能仪表检测出来的信号.特征提取就是从图像中形成的原始特征向量值非常大，如果直接把这些值送入分类器，就会给分类器造成很大的压力.不仅数据的识别速度会很慢，而且重要的是还会给数据处理的软件系统造成很大的压力，导致系统瘫痪或者使数据识别的错误概率变大.而特征提取正好解决了这个的问题，它的目的就是从众多特征中找出我们最需要的特征，把它们作为信息特征提取的特征向量，这可以看成是一种降维的过程，人体颅骨特征作为一种新的生物识别方式，它的提取一般分为两类:

(1)二维信息特征提取.如边缘、轮廓等.

(2)三维信息特征提取.主要就是颅骨的三维几何信息.

4 基于2DPCA的颅骨三维几何信息特征提取方法研究

主成分分析［3］(Principal Component Analysis，PCA)也称主分量分析，旨在利用降维的思想，把多指标转化为少数几个综合指标，是一种掌握事物主要矛盾的统计分析方法，它可以从多元事物中解析出主要影响因素，揭示事物的本质，简化复杂的问题.对于多元统计分析中，若有n个变量的m个观察值，形成一个nm的数据矩阵，n通常比较大.在实证问题研究中，为了全面、系统地分析问题，人们希望可以抓住体现事物主要特征的几个主要变量，在具体分析时，只需要将这几个变量分离出来.但是，在一般情况下，并不能直接找出这样的关键变量.这时我们可以把给定的一组相关变量通过线性变换转成另一组不相关的变量，用原有变量的线性组合来表示事物的主要方面，这就是PCA.

4.1 PCA概述

PCA分析也即主分量分析方法，用在颅骨特征提取方面它的具体步骤是:首先初始化我们的图像训练库，计算出特征向量，输入要识别的颅骨图像数据，和库里的数据进行比较，通过检查图像与特征空间的距离来进行判断，看看的图像是否是数据库中的一个，从而进行识别.

对于前面获得的颅骨的几何数据，在此用f(x，y)表示矩阵的行列信息［4］，这时实际上就相当于在二维空间对图像进行处理，而对于任意的点x、y.f正比于图像在该点的灰度值，如果把颅骨的数据集设为{Ri|i=1，…，M}，M这为图像的总个数，则这M个颅骨的平均向量为

每个颅骨图像与颅骨平均向量的差值向量是

该训练集的总体散步矩阵为

或者是

如果直接计算一个M2×M2的矩阵，那计算量是非常大的，所以要想办法减小它，在这可以构造一个矩阵，

这是个M×M的较小的矩阵，和原数据量相比，减少了很多，接着计算矩阵的特征值和特征向量，特征向量是正交归一的.这个正交归一的特征向量就是颅骨图像的特征向量.

4.2 2DPCA算法介绍［5］

假设X代表了一个m维的列向量，而这里的二维数据矩阵是一个随机的n×m矩阵，这时就可以通过有一个线性转换，把图像信息投影到X轴上，于是得出:

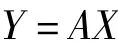
通过投影计算，就可以得出一个n×1维的向量，这个向量就是二维数据矩阵的一个特征投影向量.那么一个好的投影矩阵就显得尤为重要，实际上，可以通过计算投影向量的协方差矩阵来表示数据信息样本的总的分散量.通过分析可以获得下列的判别规则

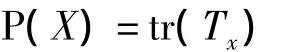
公式中的Tx代表了数据样本集的投影特征向量的协方差矩阵，通过上式可以看出，这个判别准则最重要的一点就是找到一个合适的投影方向轴，使所有数据信息投影到这个轴上的时候，所得样本总的离散度是最大的，经过分析可得，Tx可以表示为

则

如果我们设定一个矩阵Rt，

则Rt就是数据矩阵的一个离散度矩阵，而且从上式可以看出来，Rt是一个行数和列数相同的方阵，这样就可以利用数据训练样本来直接估计Rt.

假设现在一共获取了M个人的颅骨数据信息，把这些数据做为训练样本，如果第i个人的数据样本被表示成为一个m×n的矩阵，暂且把这个矩阵记为A，总的数据信息的平均向量是A1，则Rt可以表示为:

则判决规则就可以表示为:

式中的X是一个一元的特征向量，把上式这个标准看成是总的离散度准则，其中X就是我们的最优化的投影轴，换一句话说就是当准确的选择好矩阵X轴的投影以后，就能够使总样本的离散度最大化，这样就很好的压缩了样本的数据信息.但是在实际应用的过程中，只有一个最优化的轴是不够的，大多数情况下，需要选择一系列的轴，X1，X2，…，Xn，这一系列的X所对应的判别准则就是

则最优的特征轴就是Rt的正交向量所对应的前n个最大的特征值.

4.3 2DPCA提取方法介绍

前面已经介绍过了，X1，X2，…，Xn就是数据样本一系列最优的特征向量，进行图像数据的特征提取，利用的也是这几个最优特征向量.

在采用主分量分析进行特征提取之前，首先要找出样本集的一系列投影轴，这些轴可以使总样本级的离散度最大化，找出这一系列的投影轴后，就可以获得投影向量，它们分别是X1，X2，…，Xn，它们被叫做图像的主成分向量，获得的向量经常用于形成一个m×n维的矩阵，这个矩阵就叫做特征矩阵.

基于二维主成分分析的优点，速度快、简单，而且也可以较大程度的保留原始图像的数据信息，因此本文在对二维数据进行处理上，采用的是二维主成分分析算法.

4.3.1 数据分析

首先利用二维主成分分析方法对二维数据进行处理，体现在程序上采用的是MATLAB工具箱进行的，通过分析可以看出，选取投影向量时，只需要选择样本集的前n个最优特征向量就好了，而且选取的图像数据越多，所得图像就越清晰，同时恢复后的图像也越来越接近于原始图像.

4.3.2 利用主成分分析的具体实现

一般来说，采用两种方法来提取特征，一维主成分分析和二维主成分分析，为了比较，这里对两种方法都进行了比较计算，具体过程实现的流程图如图2所示.

对图像数据进行处理后，计算所有图像数据的投影轴，进行求取识别的特征向量，对于特征向量的求取方法，前面已经详细的介绍过了，这里不在做讨论.

为了分析比较，在此采用了一维和二维两种主成分分析的方法，当分类方法相同时，两种方法的识别率相差很大，并且二维主成分分析的识别率明显高于一维主成分分析，如表1所示.

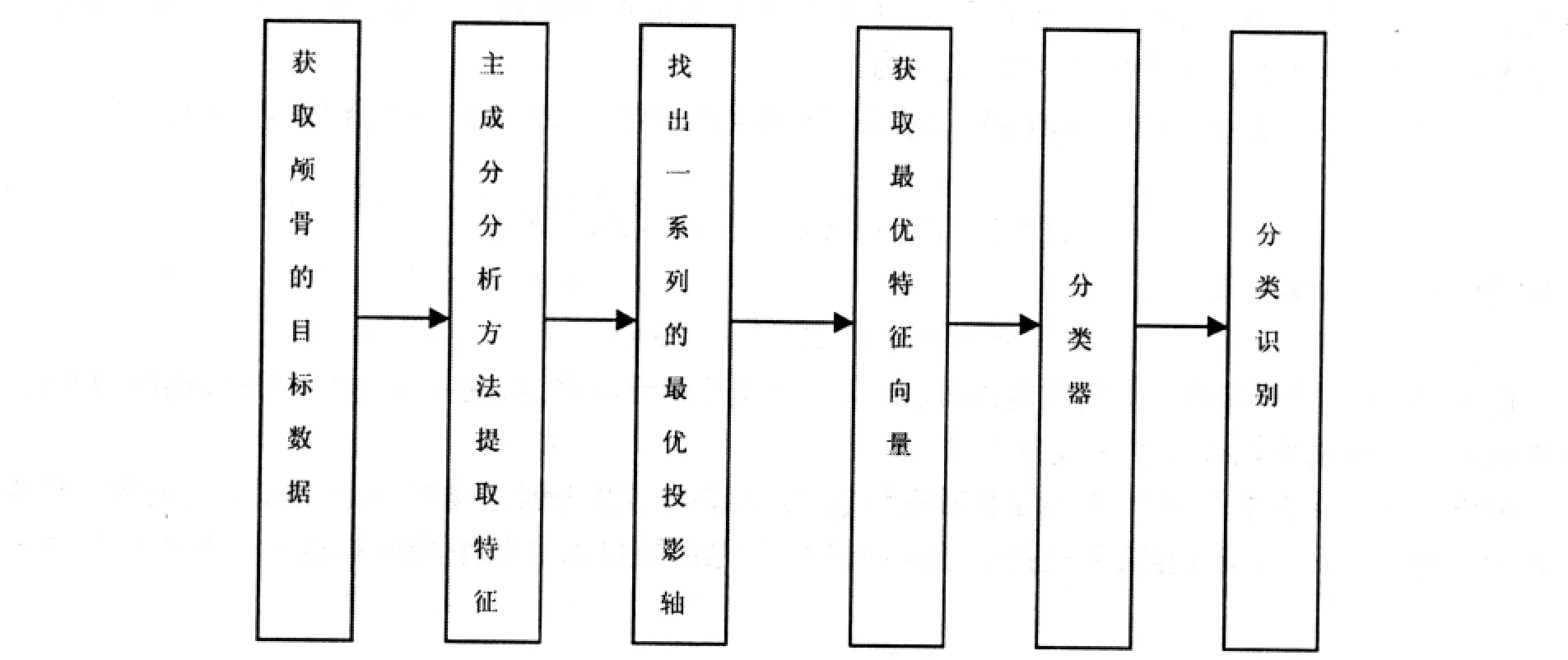
图2 流程图

表1 识别率

4.3.3 分类器的选择

在完成了特征的选择和提取后，接下来的目的就是对这些特征进行处理，对它们进行识别，识别的方法很多，但是不管是哪种方法，它们的本质是一样的，目的都是为了采用某种判别准则把特征向量进行分类，进而把物体区分开来.

一般情况下都是根据给定的特征把物体进行分类，来确定识别的物体到底属于哪个，但是现实中，因为所得的样本之间总是存在很大的相似性，所以在进行分类识别的时候，不可避免的会出现一些分类错误，在分类的过程中，不可能完全的消除它们，只能是进最大努力，使错误达到最小化，因此判断一个分类准则到底好不好的标准就是看看利用这种方法进行识别时，出现的错误率是不是最小的，这个标准是模式识别中研究的关键性的问题.因此要根据自己实际的要求选择合适的识别方法.

在进行分类识别时，可以采用的分类方法很多［6］，有最近邻法、K近邻法、神经网络法，还有贝叶斯算法，现在有些研究机构也可以研究把两种方法融合在一起，组成多类混合法.本文中采用的是最常用的分类识别方法.

最近邻法［5］进行分类的根据是:首先假设一共有w个类别，它们分别为d1，d2，…，dw，在每个表明的类别中，又有m个样本，标准规定了某类的判别函数为测试的样本与其最近的样本之间的距离值.

其中k值代表了m类样本中的第k个样本.

文中采用的是最近邻法，距离的度量值在此选取的是余弦［7］.当然也可以选择欧式距离来识别.

设Ttest为需要进行识别的图像数据信息的特征向量，Ttrain为参与训练的已知样本的特征向量值，则根据最近邻的规则，它们之间的余弦可以定义为

于是，对于最近邻法则来说，基于余弦的最近邻距离为

4.3.4 实验结果与分析

整个识别过程中，由于条件的限制，文中一共采用了18个人的颅骨切片数据信息，在这18个人中，每个人都只采集了1次，为了表格分析，这里只列出了10个人的特征识别结果，在识别过程中，每个人都进行了10次比对，通过MATLAB软件编程仿真和分析，可以看出选取的特征样本具有很好的可聚类性能，通过二维主成分分析得到的特征向量也很好的反映了数据的细节信息，识别时，能够快速的对个体做出识别，识别率也很可观，见表2所示.

表2 识别结果分析表

5 小结

文章主要介绍了图像的特征提取的定义，介绍了两种特征提取的算法，一种是一维主分量分析，一种是二维主分量分析，并分析了两者的优缺点，因为所得图像都是二维的，所以在利用二维主分量分析的时候就不用经过一个降维的处理，这样可以很好的提高识别效率，节省识别时间，所以本文中在对图像进行压缩特征提取时，采用的是二维主分量分析的方法.识别过程中，采用的是最常用的最近邻比较算法，文中是以数据的余弦作为距离的度量值，通过实验结果和分析可以看出来，利用二维主成分分析对数据进行识别有很好的识别效果，识别率达到了98.6%.

［1］边祺.模式识别［M］.北京:清华大学出版社，1998.

［2］周杰，卢春雨，张长水，等.人脸自动识别方法综述［J］.电子学报，2000，28(4):102－106.

［3］张翠平，苏光大.人脸识别技术综述［J］.中国图像图形学报，2000，5A(11):885－894.

［4］徐之海，冯华君，李奇，等.基于K－L变换的人脸识别研究［J］.光电工程，2001，28(6):48－51.

［5］胡广书.现代信号处理教程［M］.北京:清华大学出版社，2005.

［6］Yang Jian，Zhang David，Yang Jingru.Two－Dimensional PCA:A new approach to appearance－based face reprentation and recognition［J］.IEEE Trans.On Pattern Analysis Machine Intelligence，2004，26(1):131－133.

［7］段晓东，王存睿，刘向东，等.人脸的民族特征抽取及其识别［J］.计算机科学，2010，37(8):276－301.