粘弹性阻尼器对高层建筑减震效果分析

邹旭岩，郭艳坤

(中州大学工程技术学院，郑州450044)

随着我国经济的快速发展，高层、超高层建筑如雨后春笋般的一座座拔地而起。由于高层建筑结构一般刚度较柔、阻尼较小，因此，当结构的高度较高、高宽比较大时，一方面结构采用一般的抗震方法很难做到经济合理的去满足规范的要求;另一方面强烈地震时结构仍要进入弹塑性而引起结构构件的损伤与破坏。［1］因此，采用结构振动控制的方法去改善以及解决这类建筑结构的抗震设计是必要的、可行的。结构振动控制是通过调整结构动力特性的途径，来减小结构在地震等激励下的振动响应，从而保护结构以及结构附属物不受损坏。［2］结构振动控制技术依据其控制措施是否依赖外部能源可分为被动控制、主动控制、半主动控制以及混合控制。鉴于各种振动控制技术［3］的特点，本文选取在结构中设置粘弹性阻尼器(VED)的方案来进行结构减震控制。这是由于VEDs可以在较宽的频带范围内对振动进行抑制，特别适用于随机和宽带领域中动力环境的减震问题(如地震和风振)。［4，5］另外，此方法也是目前国内应用较多、较为成熟的消能减震方法;它具有价格低廉、运输、安装、使用和维护都非常方便、快捷的优点，使其能够在工程中得以实际应用。［6，7］

本文首先对一高层结构进行了多遇地震下的结构层间位移进行了验算，发现部分层间位移不满足规范要求，故采用加设VED的方案进行减震控制;接着采用工程分析软件SAP2000对加入VED的结构的动力特性进行了分析;最后对加入VED的结构在多遇地震作用下的减震效果进行了计算分析。通过以上分析，为粘弹性阻尼器在工程中的应用提供了一定的参考价值。

1．粘弹性阻尼器计算模型

目前，已提出了多种粘弹性阻尼器的恢复力模型。主要有Kelvin模型、Maxwell模型、标准线性固体模型、等效标准固体模型、等效刚度和等效阻尼模型等。［8，9］为符合振动过程中粘弹性材料的性质特征，同时考虑VED在软件中的设置问题，即采用一个粘壶单元和一个弹簧单元并联的形式，如图1所示。

1 粘弹性阻尼器计算模型

2．模型建立

本文计算结构原型为一高层建筑，共42层，标准层高为3．5 m，主要屋面高度为158．5m，结构平面为矩形，高宽比约为6∶8。建筑立面上下一致，楼层无收进和挑出。结构竖向抗侧力构件沿竖向均匀布置，部分外框架柱在二层楼面处采用梁式转换。结构计算44层(包括凸出屋面的机房)。抗震计算时，取抗震设防烈度为7度(0．1g)，建筑场地类别为Ⅱ类，设计地震分组为第一组，结构的整体阻尼比为0．04。由于本结构属于高柔结构，故利用SATWE和ETABS计算软件采用振型分解反应谱法和时程分析的计算方法进行抗震验算，发现结构Y方向存在若干层的层间位移角超出了规范规定的1/800，不能满足抗震规范的要求。现拟采用 SAP 2000对其进行计算比较，在SAP2000中所建立的模型如图2所示，并采取相应的减震控制措施使其结构满足抗震规范要求。

图2 结构计算模型

3．结构动力特性分析

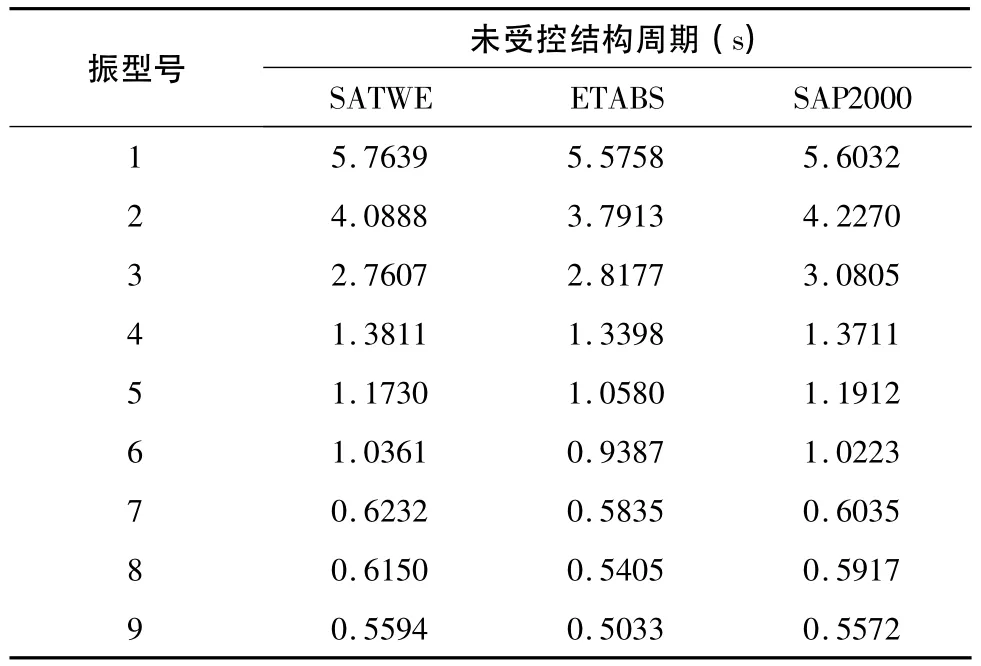
表1 结构动力特性

现将各软件动力特性分析结果列于表1中。从表中可以看出，各个软件所计算出来的各振型频率相差不大，这说明采用SAP2000所建的计算模型是正确的。

另外，对该结构进行多遇地震作用下的时程分析，根据《建筑抗震设计规范》［10］中时程分析地震波的选择要求，选择2条天然波和1条地震波加速度时程如图3所示。

图3 所选地震波加速度时程曲线

经计算发现，结构Y方向在地震作用下的层间位移角超过限值1/800的要求。主要是从18层到28层之间楼层超限，且第15、30层有位移角突变现象，因此，本文采取在15、30层部位设置VED来进行减震。

4．加入VED的结构减震效果分析

4．1 VED 布置方案

在不影响建筑正常功能使用的前提下，本文采取沿结构的边沿的柱间设置VEDs，阻尼器的参数(包括阻尼层数、剪切面积大小、剪切厚度等)根据工程所在地区的年平均气温和结构的动力特性来确定，以更好地符合结构的受力特性。阻尼器的数量、位置通过多轮时程分析进行优化调整后确定。阻尼器加设方式如图4所示，即在框架柱间和框架柱与剪力墙间加设交叉斜撑和单斜撑(如图4(a)和图4(b)所示)，以最大地发挥阻尼器的性能。另外，阻尼器在楼层平面内布置方案如图5所示。

将以上布置形式的VEDs布置在15层和30层，其立面布置按图6所示部位布置。

图4 粘弹性阻尼器布置形式

图5 VED布置方案图

图6 VED在结构中的立面布置

4．2 计算结果分析

将加入VED的结构动力特性计算结果列于表2中，从表2中可以看出:在加入 VED后，采用SAP2000计算得到结构的第一振型周期从5．05s缩短到4．65s，这说明结构的刚度由于阻尼器的加入显著提高。由此可见，VED的加入不但为结构提供阻尼，还为结构提供了一定的刚度，这也是结构层间位移可以减小的一个原因。

表2 加入VED的结构动力特性

另外，图7为结构的第一振型示意图，从图中可以看出:结构在加入VED后，结构的第一振型的位移幅值明显较未加入VED结构的小，这也说明了VED的加入使结构的刚度等特性发生了变化，从而引起了结构动力特性的改变。这也正是阻尼器产生作用的表现——振动控制的手段就是通过减振措施调整结构的动力特性，以达到减小结构在地震等激励下振动响应的目的。

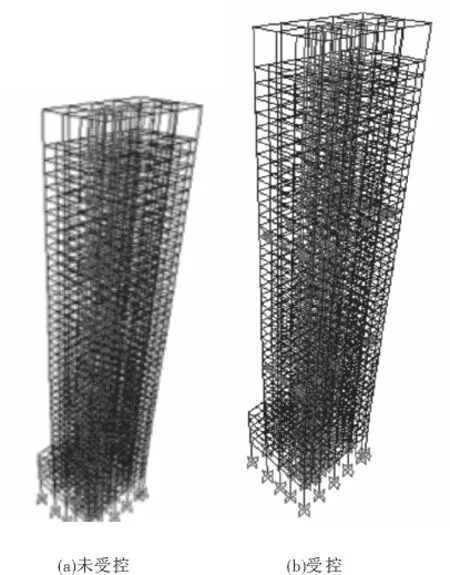
图7 结构第一振型示意图

利用SAP2000对加入VED的结构，在Elcentro、Taft和Tarzana波下进行时程分析，取15层位置的计算结果加以分析。图8为结构Y方向输入Elcentro地震波时，第15层的动力响应时程曲线。

图8 Y方向输入Elcentro波时结构的时程曲线

从图8中可以看出，结构在加入VED后，其位移响应加速度响应都得到了一定的控制。其中，位移幅值从76mm减至62mm，幅值减小了18．4%;而加速度幅值更是从2．85m/s2降至2．28 m/s2，减小了20%。这表明采用VED对结构进行减振控制的方案是可行的，并且VED装置不但为结构提供了一定的刚度，使其可以抵抗结构变形，更为结构提供了较大的阻尼，使结构的动力响应幅值得到削减。

图9为结构在加和未加VED装置计算得出各楼层的层间位移角，从图中可以看出，未加VED时，结构的层间位移角在18～28层时超出了规范的限值要求，且在15和30层有刚度突变。而在加入VED装置后，结构的层间位移得到了控制，结构的层间位移角满足规范要求。

图9 Y方向输入Elcentro波时结构的层间位移角

［1］瞿伟廉，程懋堃，毛增达．设置粘弹性阻尼器钢结构高层建筑抗震抗风设计的实用方法［J］．建筑结构学报，1998，19(3):42 －49．

［2］王肇民．高耸结构振动控制［M］．上海:同济大学出版社，1997．

［3］欧进萍．结构振动控制——主动、半主动和智能控制［M］．北京:科学出版社，2003．

［4］Xu Z D．Earthquake mitigation study on viscoelastic dampers for reinforced concrete structures［J］．Journal of Vibration and Control，2007，13(1):29 － 45．

［5］徐赵东，周云，赵鸿铁．粘弹性阻尼结构的优化设计方法［J］．西安建筑科技大学学报，1999，31(3):246 －252．

［6］郭晨光．安装粘弹性阻尼减振装置的高层建筑抗震研究［D］．西南交通大学，2004．

［7］张琴．粘弹性阻尼器控制结构地震响应的设计方法［D］．浙江大学，2003．

［8］沃德．固体高聚物的力学性能［M］．徐懋，漆宗能，等译．北京:科学技术出版社，1988．

［9］徐赵东，周洲，赵鸿铁，等．粘弹性阻尼器的计算模型［J］．工程力学，2001，18(6):73 －78．

［10］GB50011－2001．建筑抗震设计规范［S］．北京:中国建筑工业出版社，2001:111－118．