多通道SAR-GMTI通道盲均衡算法

田 斌 朱岱寅 朱兆达 司海波(南京航空航天大学电子信息工程学院 南京 210016)

②(中国人民解放军93942部队 咸阳 712000)

多通道SAR-GMTI通道盲均衡算法

田 斌*①朱岱寅①朱兆达①司海波②
①(南京航空航天大学电子信息工程学院 南京 210016)

②(中国人民解放军93942部队 咸阳 712000)

基于回波数据相关矩阵特征分解的通道盲均衡算法可有效校正多通道SAR系统中由各种非理想因素引起的通道幅度相位误差，但该算法主要的缺点是收敛速度慢。该文首先分析了基于回波数据相关矩阵特征分解的通道盲均衡算法的基本工作原理；在此基础上，针对算法收敛性差的缺点，结合降维处理技术，提出一种快速收敛的通道盲均衡算法。仿真及实测数据实验结果表明：与常规的基于回波数据相关矩阵特征分解的通道盲均衡算法相比，该文所提算法收敛所需的样本数目显著减少，即可在小训练样本条件下实现对通道幅度相位误差的均衡。

地面动目标检测；空域自适应处理；通道盲均衡；降维处理

1 引言

合成孔径雷达(SAR)是20世纪50年代初发展起来的一种新型的雷达体制。它属于主动式微波遥感设备，具有全天时、全天候和远距离成像的特点，可以大大提高雷达的信息获取能力，特别是战场感知能力，对军用和民用均有重要的应用价值。地面运动目标显示(Ground Moving Target Indication,GMTI)作为战术侦察的一部分是军用 SAR系统所必须具备的一项基本功能，也是SAR信号处理中的一个重要问题。传统的单通道SAR系统只能检测到频谱全部或部分落在杂波谱之外的运动目标。对于频谱淹没在杂波谱之内的慢动目标的检测，单通道SAR系统一般难以实现。相对于单通道SAR系统，多通道SAR系统增加了系统的空间自由度，从而可利用多个空间自由度抑制展宽的主瓣杂波，提高慢速运动目标的信杂比，获得较好的检测性能。目前常用的多通道 SAR/GMTI数据处理技术包括：沿航迹干涉(Along-Track Interferometry, ATI)技术，相位中心偏置(Displaced Phase Center Antenna,DPCA)技术和空时自适应处理(Space Time Adaptive Processing, STAP)技术等[1−6]。

在多通道 SAR/GMTI数据处理技术的基础理论研究中，往往假定系统中各个通道响应是一致的，这时采用上述几种方法均可获得良好的地面运动目标检测性能。然而，在实际应用中，它们的检测性能都受到雷达系统特性的影响，例如图像配准误差、天线位置误差、通道幅度相位误差等。这些非理想因素将会直接影响SAR图像之间的相干性，进而影响杂波抑制性能。为了提高系统的杂波抑制性能，通常都会在进行杂波抑制之前对主辅通道进行通道均衡，以消除通道间的幅度相位不一致性。传统的多通道雷达自适应均衡方法[7,8]是通过在接收机前端注入校准信号来实现通道均衡，其缺点是只能均衡接收机部分的不一致，而对于天线到接收机前端的馈线部分的不一致则无法校正。为此，文献[9-12]提出利用基于回波数据相关矩阵特征分解的通道盲均衡算法进行通道均衡，该算法利用信号处理方法解决通道均衡问题，有效克服自适应均衡算法的上述缺点。

基于回波数据相关矩阵特征分解的通道盲均衡算法在具体实现时，首先根据训练样本数目的要求从待均衡单元的相邻单元中选取若干单元作为训练样本来估计待均衡单元杂波的协方差矩阵；然后，对样本协方差矩阵作特征分解，得到相应的主特征向量；最后，将待均衡单元数据矢量的各分量除以主特征向量的相应分量来达到均衡通道幅度相位误差的目的。基于回波数据相关矩阵特征分解的通道盲均衡算法虽然能有效地校正由各种非理想因素所造成的通道幅度相位误差，但该算法存在收敛速度慢的缺点，即估计样本协方差矩阵时需要大量的训练样本，特别是当协方差矩阵维数较大时这一缺点尤为突出。本文首先对基于回波数据相关矩阵特征分解的通道盲均衡算法的基本工作原理进行了分析；在此基础上，针对算法收敛性差的缺点，结合降维处理技术，提出一种快速收敛的通道盲均衡算法。仿真及实测数据实验结果表明：与常规的通道盲均衡算法相比，本文所提算法收敛所需的样本数目显著减少，即可在小训练样本条件下实现通道误差均衡。

2 多通道SAR回波模型

多通道 SAR系统沿航迹方向等间隔排布N个接收孔径(通道)，不失一般性，假定通道 1为发射通道(参考通道)，其余通道为接收通道。数据处理时，首先对各通道接收的回波数据分别进行SAR成像处理；其次，根据惯导系统提供的平台运动参数及 SAR成像几何关系补偿由接收天线位置不同引起的固定相位差。完成上述处理后，将各通道对应地面 (x0,y0)处的成像结果排成一列，构造空域采样信号矢量Z(x0,y0)，其中x0,y0分别表示距离与方位坐标。在H0(无目标信号，只有杂波和内部热噪声)和H1(既有目标信号，又有杂波和噪声)二元假设下，Z(x0,y0)可表示成如下形式：

其中M表示参与估计的样本数。为保证输出信杂噪比的损失不超过3 dB，用来估计协方差矩阵的样本数M应该大于等于2N−3。将此协方差矩阵估计值代替式(3)中的真实值便可完成权矢量的计算，从而可实现杂波的抑制。

在实际的工程应用中，由于各种非理想因素的影响，各通道之间往往存在幅度相位误差，该误差会在一定程度上影响上述方法的杂波抑制性能。因此，为了得到较为满意的杂波抑制性能，各通道间的误差必须得到有效地补偿。下面我们首先对基于回波数据相关矩阵特征分解的通道盲均衡算法进行了介绍。在此基础上，针对该算法收敛性差的缺点，提出了一种快速收敛的通道盲均衡算法。

3 快速收敛的通道盲均衡算法

3.1基于回波数据相关矩阵特征分解的通道盲均衡算法

3.2 快速收敛的通道盲均衡算法

在理想的情况下，传统的通道盲均衡算法只要2N个独立同分布的训练样本便可对杂波实际空域导引矢量进行较为准确的估计。在实际的SAR图像中，由于杂波背景总是体现出一定的非均匀性，这时估计杂波实际空域导引矢量所需要的训练样本数目往往会大于2N[9−11]。可见，传统的通道盲均衡算法在实际应用中其收敛性较差，尤其是当通道数目N较大时这一缺点尤为突出。为了有效解决上述问题，本文提出一种快速收敛的通道盲均衡算法，该算法的核心思想是利用降维处理技术来减少估计杂波实际空域导引矢量所需的训练样本数目，其具体实现过程可概括如下：

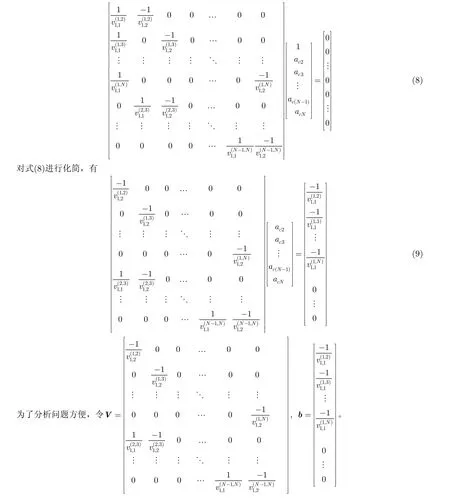
对于快速收敛的通道盲均衡算法来讲，求解ac的过程也就是寻找上述线性约束方程组的解。考虑到矩阵方程式(9)为超定方程(overdetermined equation)[14]，即方程个数多于未知参数个数，因此，可利用最小二乘法对杂波实际空域导引矢量ac进行估计。在最小二乘准则下，待均衡像素单元的杂波实际空域导引矢量ac的估计值可表示为

式中Vl−表示矩阵V的最小二乘广义逆。在实际处理中，可以利用 Ganss-Newton法或阻尼最小二乘法来求解得到，详细的求解过程请参考文献[15]，在此不再赘述。在获取得到后，将Z(x0,y0)的各分量除以的对应分量便可实现通道误差均衡。

3.3 两种通道盲均衡算法的性能对比

下面分别采用常规的通道盲均衡算法和本文所提算法对待均衡像素单元的通道幅度相位误差进行了估计及补偿，并对两种算法补偿性能进行分析和比较。系统仿真参数如下：接收孔径个数N为 8，输入杂噪比为CNR=15 dB，杂波的理想空域导向矢量=[1,1,… , 1]T。仿真过程中，我们分别对各接收通道(除参考通道)加入均值为1.25、均方差为0.1的随机幅度误差，及均值为5o、均方差为2o的随机相位误差。

表1分别列出了不同样本数目条件下经两种通道盲均衡算法补偿后待均衡像素单元的通道幅度误差的均值、均方差及通道相位误差的均值、均方差。从表1中容易看出：(1)在给定的样本数目条件下，两种通道盲均衡算法均能对待均衡像素单元的通道误差进行不同程度的补偿；(2)常规的通道盲均衡算法虽然能对通道误差进行有效的补偿，但往往要求训练样本个数大于或等于2N，当训练样本数较小时，算法的补偿性能将显著下降；(3)与常规的通道盲均衡算法相比，由于本文所提算法采用了降维处理技术，从表中的补偿结果可以看出，本文所提算法在小训练样本条件下便可对待均衡像素单元的通道误差进行较为准确的补偿，该仿真结果与上节的理论分析基本保持一致。由此可见，快速收敛的通道盲均衡算法有效减少了估计通道误差所需的训练样本数目，提高了常规通道盲均衡算法的收敛性能，为多通道 SAR-GMTI的通道盲均衡提供了一种新的技术途径。

4 实测数据处理

本节，为验证新算法的有效性，本文对某型机载三通道沿航迹干涉SAR的试飞数据进行了处理。试验中，雷达工作在X波段，飞机高度为5300 m，飞行速度为 110 m/s，天线相位中心到成像区中心的距离为22464 m，发射LMF信号带宽180 MHz，脉冲重复频率1250 Hz，孔径之间距离0.7 m。地面场景中，5个地面配合目标行驶在一段车辆相对较少且笔直的乡间小道上，其中有两辆车的方向与另外3辆的方向相反，5辆车的车速控制在1～7 m/s。图1给出了经过位置配准后的地面成像区域的SAR图像，由于3个通道的SAR图像相似，因此只给出了中心通道的图像。

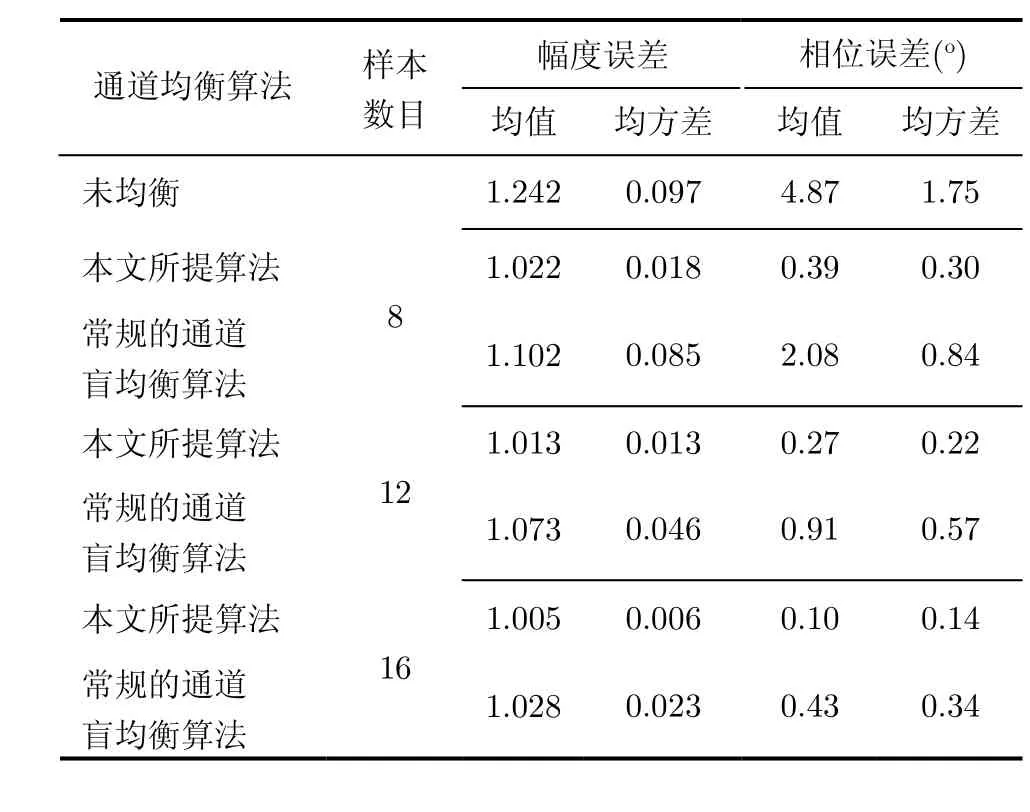
表1 均衡前后待均衡像素单元通道幅度和相位误差对比

图1 目标所在区域的SAR图像

图2给出了未进行通道误差校正时通道幅度和相位响应随方位像素单元变化曲线。图 2(a)中，为了更为直观的比较3个通道的幅度响应，我们以通道1的幅度响应为基准分别对通道2和通道3的幅度响应进行了归一化处理；图 2(b)中，分别给出了通道1和通道2及通道1和通道3的干涉相位差随方位像素单元变化曲线。在对实测数据进行通道均衡处理时，需要注意的是：训练样本中包含干扰目标往往是难以避免的，例如当某一单元存在目标信号，而在均衡其它单元用其作为训练样本时，目标信号就成为干扰信号。对于常规的通道盲均衡算法和本文所提算法而言，其有效性通常都会受干扰信号污染影响，特别在强干扰信号污染情况下将不能获得正确的校正结果。为了降低强干扰信号污染的影响，文献[12]在常规的通道盲均衡算法的基础上给出了一种简单有效的处理方案，即在估计样本协方差矩阵之前，对空域采样信号矢量以通道1为参考进行模归一处理。本文在通道均衡过程中同样也采用该处理方案来降低强干扰信号对本文所提算法性能的影响。图3给出了经本文所提算法校正后通道的幅度和相位响应图，估计通道误差所使用的样本数目为20。从图3(a)和3(b)中可以看出，经本文所提算法校正后，各通道的通道误差在很大程度上都得到了有效的补偿，3个通道对应像素单元的幅度和相位响应也基本上趋于一致。为了进行对比分析，本文同样采用了常规的通道盲均衡算法对数据进行了处理，其相应的处理结果如图4所示。从处理结果容易看出，在相同的样本条件下，常规的通道盲均衡算法的通道误差补偿性能要劣于本文所提算法。

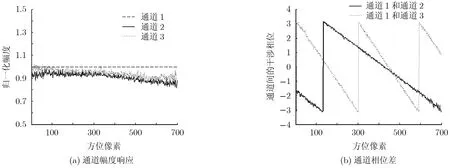
图2 通道误差未校正时通道的幅度响应和相位响应

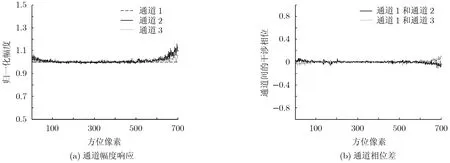
图3 经本文所提算法校正后的通道幅度和相位响应

在完成通道误差校正处理后，采用空域自适应处理对SAR图像中的杂波进行抑制，设估计权矢量所使用的训练样本个数为10。图5(a)和5(b)分别给出了经常规的通道盲均衡算法和本文所提算法校正后的空域自适应滤波处理的输出结果图。图中，用白色的阿拉伯数字标识的是试验中的地面配合目标车辆。对比图5(a)和5(b)可以看出，图5(b)中的杂波剩余显然低于图5(a)中的，尤其是A区所示的杂波剩余，此实验结果也进一步验证了本文所提算法的优越性。

5 结论

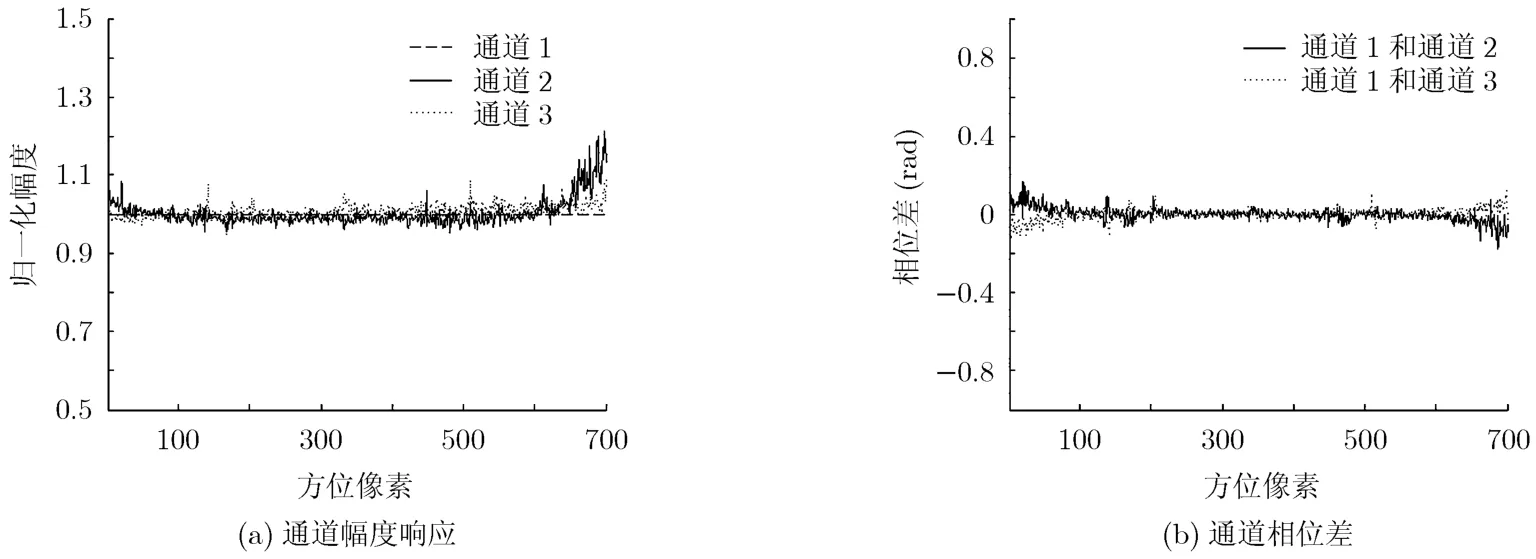
图4 经常规的通道盲均衡算法校正后的通道幅度和相位响应

图5 空域自适应滤波处理的输出结果图

基于回波数据相关矩阵特征分解的通道盲均衡算法常用来校正多通道SAR系统的通道误差。本文首先对基于回波数据相关矩阵特征分解的通道盲均衡算法的基本工作原理进行了分析；在此基础上，针对算法收敛速度慢的缺点，结合降维处理技术，提出一种新的通道盲均衡算法。与常规的通道盲均衡算法相比，本文所提算法收敛所需的样本数目显著减少，即可在小训练样本条件下实现对通道误差均衡。仿真及实测数据实验结果验证了该算法的有效性和优越性。

[1] Barber B C and Barker J E. The use of SAR-ATI for maritime surveillance and difficult target detection [C].Proceeding of 2009 IEEE National Radar Conference,Bordeaux, France, 2009: 1-6.

[2] Cerutti-Maori D, Gierull C H, and Ender J H G.Experimental verification of SAR/GMTI improvement through antenna switching [J].IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(4): 2066-2075.

[3] Sun Hua-dong, Zhang Li-zhi, and Jin Xue-song. Parameter estimations based on DPCA-FrFT algorithm for three channel SAR/GMTI system [C]. The 2011 International Conference on Intelligent Computation Technology and Automation, Shenzhen, China, 2011: 640-644.

[4] Sikaneta I C and Gierull C H. Adaptive CFAR for space-based multi-channel SAR/GMTI [C]. The 8th European Conference on Synthetic Aperture Radar, Aachen,Germany, 2010: 1-4.

[5] 吴迪, 朱岱寅, 朱兆达. 基于改进FRACTA算法的多通道SAR动目标检测技术[J]. 电子与信息学报, 2010, 32(9):2179-2183.

Wu Di, Zhu Dai-yin, and Zhu Zhao-da. Moving target detection for multi-channel SAR based on improved FRACTA algorithm [J].Journal of Electronic&Information Technology, 2010, 32(9): 2179-2183.

[6] Wang Ling, Zhen Lu-gui, and Guan Ya-lin. Novel space-time processing method for airborne SAR to detect and image the slowly moving targets [C]. 2010 Third International Joint Conference on Computational Science and Optimization,Huangshan, China, 2010: 435-439.

[7] Wu Shun-jun and Li Ying-jun. Adaptive channel equalization for space time adaptive processing [C]. IEEE International Radar Conference, Lexandria, 1995: 624-628.

[8] 彭小亮, 李荣峰, 王永良, 等. 两种修正的自适应通道均衡方法[J]. 电子与信息学报, 2006, 28(6): 658-662.

Peng Xiao-liang, Li Rong-feng, Wang Yong-liang,et al.. Two method of modified adaptive channel equalization [J].Journal of Electronic&Information Technology, 2006, 28(6):658-662.

[9] Koerbor M A and Funhrmann D R. Radar antenna calibration using range-Doppler data [C]. IEEE 7th SP Workshop on Statistical Signal & Array Processing, Quebec,1994: 441-444.

[10] Ender J H G. Space time processing for multichannel synthetic aperture radar [C]. IEE Colloquium on Space Time Adaptive Processing, London, 1998: 611-618.

[11] 杨志伟, 廖桂生, 曾操. 基于雷达回波数据相位矢量的通道盲均衡[J]. 电子学报, 2008, 36(9): 1682-1686.

Yang Zhi-wei, Liao Gui-sheng, and Zeng Cao. Blind channel balance using phase vector of echoes [J].Acta Electronica Sinica, 2008, 36(9): 1682-1686.

[12] 周争光, 廖桂生, 朱圣棋. 一种对强目标信号污染稳健的自适应通道盲均衡算法[J]. 西安电子科技大学学报, 2009, 36(6):1103-1107.Zhou Zheng-guang, Liao Gui-sheng, and Zhu Sheng-qi.Robust channel blind balance approach to strong target signals contamination [J].Journal of Xidian University, 2009,36(6): 1103-1107.

[13] 张小飞, 汪飞, 徐大专. 阵列信号处理的理论和应用[M]. 北京: 国防工业出版社, 2010: 26-27.

[14] 张贤达. 现代信号处理[M]. 第 2版, 北京: 清华大学出版社,2002: 56-57.

[15] 范钦珊. 数学手册[M]. 北京: 高等教育出版社, 2000:112-114.

Channel Blind Equalization Algorithm for Multi-channel SAR/GMTI System

Tian Bin①Zhu Dai-yin①Zhu Zhao-da①Si Hai-bo②
①(College of Electronics and Information Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing210016,China)
②(Troop93942of PLA,Xianyang712000,China)

Channel blind equalization algorithm based on Eigen-Decomposition (ED) of data covariance matrix can be applied to calibrate the channel mismatch for multi-channel SAR/GMTI system. However, this algorithm has a disadvantage that it suffers from a slow convergence rate. In this paper, the principle of channel blind equalization algorithm is firstly investigated. Then, to improve its convergence rate, reduced-dimension technique is used into this algorithm and a new channel blind equalization algorithm is proposed. Experimental results on simulation data and measured SAR data demonstrate that compared with the conventional channel blind equalization algorithm, the proposed algorithm shows a fast convergence rate and is able to calibrate channel mismatch with much less sample support.

Ground moving target detection; Space adaptive processing; Channel blind equalization; Reduceddimension technique

TN957.51

A文章编号：1009-5896(2012)06-1324-07

10.3724/SP.J.1146.2011.00723

2011-07-14收到，2012-03-14改回

国家自然科学基金(61071165)和教育部新世纪优秀人才支持计划(NCET-09-0069)资助课题

*通信作者：田斌 Tianbin218@163.com

田 斌： 男，1983年生，博士生，研究方向为地面慢动目标检测.

朱岱寅： 男，1974年生，教授，博士生导师，研究方向为雷达成像与信号处理.

朱兆达： 男，1939年生，教授，博士生导师，研究方向为雷达信号检测与处理.

司海波： 男，1983年生，研究方向为雷达制导.