基于频率变换的双通带腔体滤波器的研究

寇 鑫 肖中银 黄春艳 李 好 储君君

(上海大学特种光纤与光接入网省部共建重点实验室 上海 200072)

基于频率变换的双通带腔体滤波器的研究

寇 鑫*肖中银 黄春艳 李 好 储君君

(上海大学特种光纤与光接入网省部共建重点实验室 上海 200072)

该文基于频率变换的方法设计了两种结构的双通带的腔体滤波器，一种是通过谐振器之间直接耦合实现的；另一种是在谐振器之间引入交叉耦合实现的，从而达到产生传输零点的目的。首先根据设计指标，采用频率变换的方法，计算得到谐振器间的耦合系数和外部Q值，然后利用Ansoft HFSS建立同轴腔体滤波器的模型并进行仿真，仿真结果与ADS中等效电路得到的理论结果基本吻合，从而验证了这种方法的正确性。最后通过对级联型结构与交叉耦合型结构双通带腔体滤波器的比较，得出后者比前者具有更好的带外抑制特性。

腔体滤波器；双通带；频率变化；交叉耦合

1 引言

射频多通带滤波器是射频系统中不可缺少的关键器件之一，它能有效地滤除无线通信系统中的干扰信号，降低各个频道之间的干扰，从而保证各个频段的正常通信。随着无线通信与移动通信的迅速发展，从早期的2G通信到现在的4G通信以及无线局域网(WLAN)和无线城域网(WIMAX)的出现，频段划分得越来越细，这对滤波器的带外衰减提出了更高的要求。早期，采用带通滤波器与带阻滤波器的级联来设计双频滤波器[1]，不过这种方法包含了两种滤波器，增加了滤波器的整个体积；另一种方法是将两个带通滤波器并联起来实现双频滤波[2]，这种结构不仅体积大而且插入损耗也大；还有学者在通带滤波器中引入一个传输零点，从而形成双通带[3]，但是这种方法是基于数值优化的方法，收敛性得不到保证。目前，除了对基片集成波导双频带滤波器的研究[4]，更主要集中在微带双通带滤波器的研究，而且大多数的实现方式都是集中在对微带滤波器的结构的改进[5−7]。然而大多数的双通带微带滤波器设计时只考虑了中心频率，对带宽这一指标很少有文献涉及到，这主要是由于微带谐振器之间的耦合比较难控制，而基于频率变换的腔体滤波器则可以有效地控制带宽。腔体滤波器具有高Q值，功率容量高，带外衰减陡峭，带宽窄等优点，广泛应用于无线通信和卫星通信中。目前国内、国外涉及腔体滤波器的文献多数是关于单通带的[8,9]，双通带的比较少，因此本文基于频率变换的方法设计了两种结构的四阶的双通带腔体滤波器，带宽和衰减度都可以得到很好的控制。首先将双通带滤波器的指标采用频率变换的方法，将其转换为归一化低通原型滤波器的指标，综合出归一化低通滤波器原型，然后由频率变换得到双通带滤波器与归一化低通滤波器的元件对应关系，从而得到双通带滤波器的电路拓扑结构，求出谐振器之间的耦合系数以及源和负载的有载Q值的大小，最后利用HFSS设计出频率范围在2.50-2.52 GHz和2.55-2.57 GHz的两种不同结构的双通带腔体滤波器，仿真结果与理论结果基本吻合。

2 频率变换

图1 由双通带到单通带的频率变换

式中定义的b1,b2,ω01,ω02为频率变换的参数。通过这种转化后，归一化原型电路中的单个电容变换为双通带中的谐振器，如图2所示。

通过频率变换，ω域中的上边频ωL1,ωL2被映射到Ω域的-1上，而下边频ωH1,ωH2映射到Ω域1

图2 由单通带到双通带的元件转换

当所有参数被确定后，图2中双通带的谐振器也就被确定，因此双通带滤波器的整个等效电路也就被确定了，如图3所示，其电路拓扑结构如图4所示。

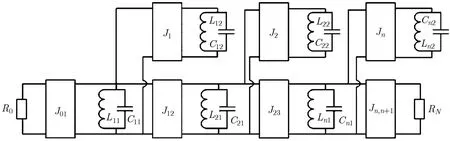
图3 双通带滤波器的等效电路

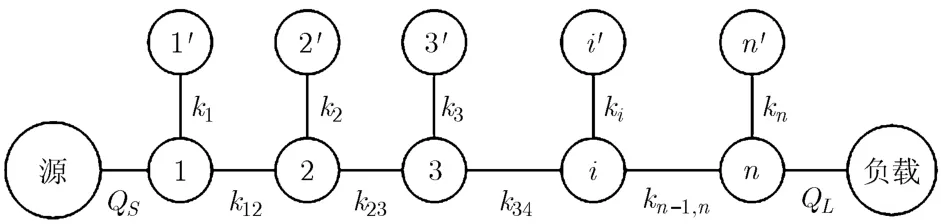
图4 双通带滤波器的电路拓扑结构

从图3和图4的等效电路和拓扑结构可以求得谐振器1～n之间的耦合系数ki.i+1，谐振器i和i′之间的耦合系数k，以及源和负载的外部品质因数。

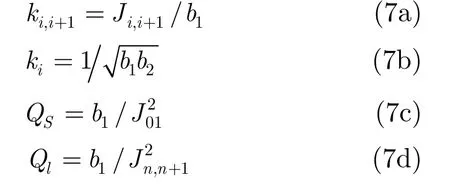
3 双通带腔体滤波器的设计

根据前面的理论分析，设计了两种不同结构的四阶腔体滤波器：一种是级联型结构，另外一种是交叉耦合型结构，且这两种结构的第1通带范围是2.50-2.52 GHz，第2通带范围是2.55-2.57 GHz，每个通带的带宽为20 MHz，回波损耗≥20dB。首先在ADS中进行原理电路的仿真，然后通过HFSS进行建模。

3.1 级联型结构与交叉耦合型结构

四阶级联型结构和交叉耦合型结构的双通带腔体滤波器的电路拓扑结构分别如图5(a)和图5(b)所示。根据给定的指标，两种结构的耦合系数以及源和负载的品质因数可以通过式(7)计算分别得到。

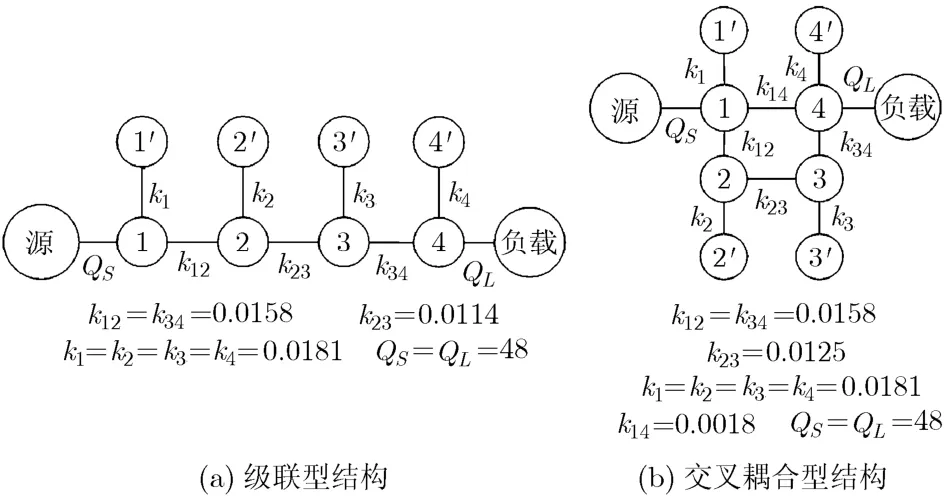
图5 四阶双通带滤波器的电路拓扑结构

3.2 在ADS中建立原理电路

当耦合系数和品质因数确定后就可以在 ADS中分别建立级联型双通带腔体滤波器的原理电路和交叉耦合型的原理电路，如图6所示。

3.3 在HFSS中建立仿真模型

首先在HFSS中建立单腔仿真模型，通过本征模求解方式进行仿真，确定单腔谐振器的高度；然后再建立双腔仿真模型，根据耦合系数的值，确定腔间耦合窗口的大小以及耦合金属板的大小；最后根据图5的电路拓扑结构建立级联型和交叉耦合型的双通带腔体滤波器的模型，如图7所示。其中矩形腔边长a=20 mm，高b=30 mm，谐振圆柱的半径r=4 mm，其它具体尺寸大小如表1和表2所示。

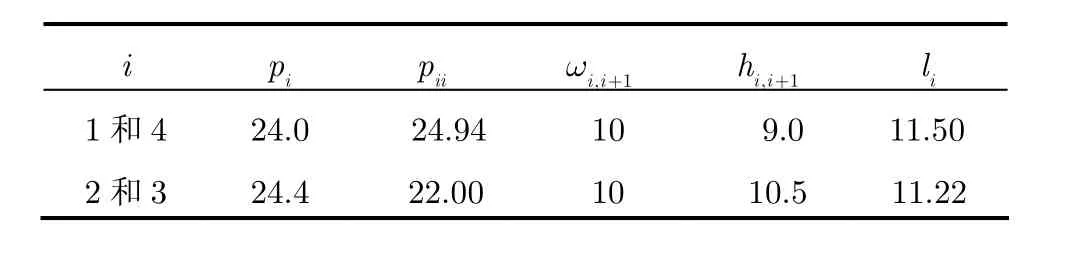
表1 级联型结构的双通带滤波器尺寸参数(mm)

表2 交叉型结构的双通带滤波器尺寸参数(mm)

表1和表2中的pi为图5中电路拓扑结构的谐振圆柱1～4的高度，pii为谐振器1′～4′的高度，ωi,i+1为谐振器i和i+1间耦合窗口的宽度，hi,i+1为其耦合窗口的深度，li为谐振器i和i′间耦合金属板的长度。对于交叉耦合滤波器，除了表2中的滤波器的尺寸大小，谐振器1和4之间还存在交叉耦合，其耦合窗口的宽度ω1,4= 10 mm,h1,4= 15 mm。

4 仿真结果分析

图8给出了图6中原理电路的理论结果与图7中模型电路的仿真结果的比较曲线。由于仿真模型可调参量比较多，通过仿真得到理想的曲线比较困难，但通过以下两图的比较发现滤波器的理论结果与仿真结果吻合良好。两种结构滤波器的第1通带频率在2.50-2.52 GHz，第2通带频率在2.55-2.57 GHz，很好地控制了带宽范围，带内插损均小于 1 dB，回波损耗均大于20 dB，基本实现了滤波器的设计指标。

图9给出了两种结构双通带滤波器的仿真结果曲线。很明显可以看出交叉型结构比级联型结构带外衰减陡峭，频率选择性更好。这主要是由于该结构在谐振器1和4之间引入了交叉耦合，从而在带外产生了一对衰减零点。

5 结束语

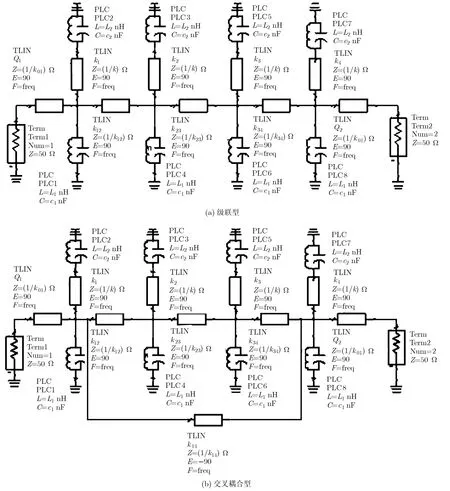
图6 双通带滤波器原理电路

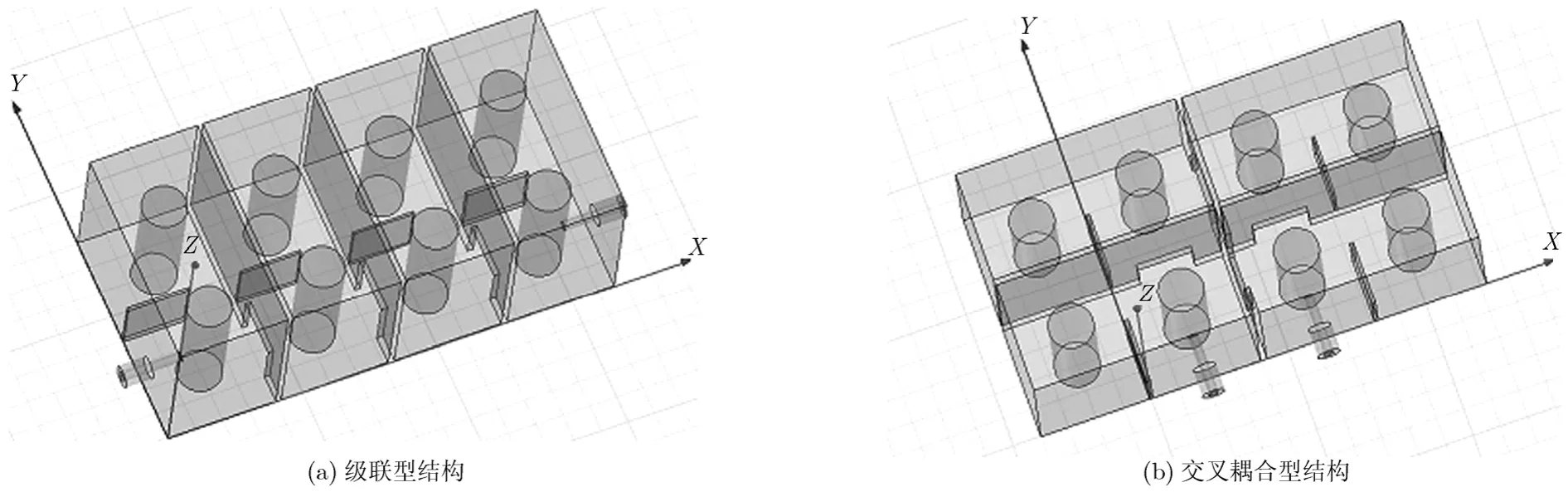
图7 双通带腔体滤波器模型

图8 滤波器S参数的理论结果与仿真结果比较 图9 级联型与交叉型结构滤波器的仿真结果曲线比较

本文基于频率变换的方法设计了两种结构的双通带腔体滤波器。给定滤波器的通带范围，得到了耦合系数以及源和负载的有载Q值，在此基础上，利用3维仿真软件建立了腔体滤波器的模型，仿真结果与理论结果吻合良好，并且，该滤波器很好地控制了频带范围，证明了该方法的可行性。并在最后通过对级联型结构与交叉耦合型结构的比较，得出后者比前者在其他情况相同的条件下，带外衰减更陡峭，在工程中更具有实际意义。

[1] Tsai L C and Hsue C W. Dual band bandpass filters using equal-length coupled-serial-shunted lines and Z-transform technique[J].IEEE Transactions on Microwave Theory and Techniques, 2004, 52(4): 1111-1117.

[2] Huang C L and Pan C L. Dual-band multiplayer ceramic microwave bandpass filter for application in wireless communication[J].Microwave and Optical Technology Letters,2002, 32(5): 327-329.

[3] Lee J, Uhm M S, and Yom I B. A dual-passband filter of canonical structure for satellite applications[J].IEEE Microwave and Wireless Components Letters, 2004, 14(6):271-273.

[4] Shen W, Sun X W, Yin W Y,et al.. A novel single-cavity dual M-mode substrate integrated waveguide filter with non-resonating node[J].IEEE Microwave and Wireless Components Letters, 2009, 19(6): 368-370.

[5] Shi J and Xue Q. Novel balanced dual-band bandpass filter using coupled stepped-impedance resonators[J].IEEE Microwave and Wireless Components Letters, 2010, 20(1):19-21.

[6] Chiou Y, Wu C, and Kuo J T. New miniaturized dual-mode dual-band ring resonator bandpass filter with microwave C-sections[J].IEEE Microwave and Wireless Components Letters, 2010, 20(2): 67-69.

[7] 朱永忠, 谢拥军, 倪大宁. 含源-负载交叉耦合的准椭圆函数滤波器设计[J]. 电子与信息学报, 2008, 30(3): 604-606.

Zhu Yong-zhong, Xie Yong-jun, and Ni Da-ning. Design of quasi-elliptig filter with sourece-Load cross-coupling[J].Journal of Electronics&Information Technnology, 2008,30(3): 604-606.

[8] 费洪磊, 唐普英. TD-SCDMA A频段交叉耦合腔体滤波器的设计与实现[J]. 固体电子学研究与进展, 2011, 31(22):152-154.

Fei Hong-lei and Tang Pu-ying. Design and implementation of cross-coupled cavity filter for TD-SCDMA A band[J].Research and Progress of SSE, 2011, 31(22): 152-154.

[9] Wang Y and Yu M. True inline cross-coupled coaxial cavity Filters[J].IEEE Transactions on Microwave Theory and Techniques, 2009, 57(12): 2958-2965.

[10] Macchiarella G and Tamiazzo S. Design techniques for dual-passband filters[J].IEEE Transactions on Microwave Theory and Techniques, 2005, 53(11): 3265-3271.

Design of Dual-band Cavity Filter Using Frequency Transformation Method

Kou Xin Xiao Zhong-yin Huang Chun-yan Li Hao Chu Jun-jun
(Key Laboratory of Specialty Fiber Optics and Optical Access Networs,Shanghai University,Shanghai200072,China)

This paper presents two different dual-band cavity filters based on the frequency transformation. The cavity filters have two different configurations. The one is presented by directed coupling between adjacent resonators, and the other one is presented by introduced cross coupling between nonadjacent resonators to generate a pair of transmission zeros. At first, according to the filter specification the coupling coefficients between resonators and the external quality factors are calculated and obtained. Then the model of the dual-band cavity filters are established with Ansoft HFSS, the simulation result agrees well with the result of equal circuit in ADS,indicating that this method is correct and feasible. Finally, the comparison between the cascade type structure and cross coupling type structure shows that the later has more excellent stopband performance.

Cavity filter; Dual-band; Frequency transformation; Cross coupling

TN713

A文章编号：1009-5896(2012)06-1489-05

10.3724/SP.J.1146.2011.01151

2011-11-07收到，2012-01-11改回

国家自然科学基金(61077068)，上海市自然科学基金(10ZR1411900)和上海市重点学科及实验室基金(S30108, 08DZ2231100)资助课题

*通信作者：寇鑫 296130731@qq.com

寇 鑫： 男，1987年生，硕士生，研究方向为腔体滤波器.

肖中银： 男，1964年生，副教授，硕士生导师，博士，研究方向为微波与毫米波电路等.

黄春艳： 女，1987年生，硕士生，研究方向为微带滤波器.