基于石英晶体的微质量测量方法研究

2012-01-26周俊鹏王连明

物理实验 2012年6期

杨明，周俊鹏，王连明

（1．吉林省广播电视技术中心台，吉林长春130021；2．东北师范大学物理学院，吉林长春130024）

1 引言

微小质量的测量在物理、化学、生物等领域的研究中有重要的作用，精确的测量数据是理论产生的保证．而微小质量的精确测试始终是一个难题，国内外现有的微小质量测量方法主要可分为两大类：传统的电子天平测量法和新型的谐振式微质量测量法．

电子天平测量技术经过多年发展已经较成熟．总体设计思路是将被测物体重力转化为电磁力、电压或者光通量等其他物理量，再借助转换量测量出被测物体质量．国际先进水平精度可达到0．01 mg［1］．新型的谐振式测量方法主要以石英晶体作为主要检测元件，此测量方法具有响应速度快、稳定性好、抗腐蚀耐放射、成本低廉等特点，精度可以达到ng［2］，并且易于用单片机、FPGA等数字芯片进行控制和数据测量［3］．

由此可见，基于晶体谐振的测量方法精度远高于现有研究用电子天平，更适合于各种微小物质的测量和分析．目前，国内基于晶体谐振的微质量测量方法刚刚起步，本文将理论分析与实验相结合，对这种测量方法展开研究．

2 石英晶体质量敏感原理

晶体是由分子或原子在空间按一定规律周期

其中：f0为晶体的基频，Δf为晶体谐振频率的变化量；Δm为电极表面的质量变化量；A为电极的接触面积，根据电极的形状而定；ρq为石英的密度，一般ρq＝2 651 kg／m3；cq为石英的压电强化切变模量，对于通用的 AT 切变方式［7－8］，cq＝2．93×1010N／m2．AT切割是指沿着与石英晶体主光轴（Z轴）成35°15′切割得到的石英晶体振荡片，这种切割方法加工的晶体有良好的温度特性，是制造石英晶体元件最常用的方法［5－6］．

由式（1）可以看出，对于已经标准AT切割的重复地排列所构成的固体物质．晶体内部微粒的周期性排列结构是晶体最基本的特征．1880年，居里兄弟发现在各向异性的石英晶体表面上施加一定的压力之后，晶体两表面之间产生与压力成正比的电压．这一现象后来被叫做正压电效应．而如果在晶体两端加上电场，晶体内部电偶极矩会被拉长，产生机械形变，从而将电能转化为机械能，这种现象叫做逆压电效应［3］．

1959年，德国科学家Sauerbrey首先研究了气相中石英晶体表面吸附的微小质量和其频率偏移的关系，并最终进行了实验验证，推导出了质量吸附和晶体谐振频率偏移的关系式，这就是著名的Sauerbrey公式［4］．如式（1）所示晶片，在假定外加质量均匀刚性地附着于晶片的表面的条件下，晶片的谐振频率变化与外加质量成正比关系．

虽然Sauerbrey公式是在真空的条件下得出的，但也适用于常温常压非真空条件．在实际应用中除了方程中指出的涂层质量对石英晶体的频率变化有影响外，温度、接触面粗糙程度和固定夹具的材料等都对频率变化有影响．以下情况不能用Sauerbrey公式：

1）被吸附的物质在电极表面上呈非刚性状态（所谓刚性是指2个物体相碰撞不会发生变形），因此2个刚体就不会占据同一个空间；

2）被吸附的物质在电极表面上不固定，出现滑动；

3）被吸附的物质在电极表面上沉积不均匀．

Sauerbrey公式的提出为晶体在微质量测量领域的应用奠定了理论基础［7－8］．

3 石英晶体振荡电路的设计

石英晶体在电气上可以看作1个等效电容C1，1个等效电阻R1和1个等效电感L1相串联，再并联1个介质电容C0的二端网络，如图1框中电路所示．

图1 石英晶体振荡电路

等效电路两端之间的阻抗非常小的频率一般称为谐振频率，也叫串联谐振频率fs．阻抗最大时的频率称为逆谐振频率，也叫并联谐振频率fp．在晶体谐振时可以忽略等效电阻R1（电阻值一般在数10Ω以下），并且认为C1≪C0（C1值约为10－2～10－1p F，C0的值约为几个或几十个p F）［9］．可以得出频率表达式为

式（4）中f0指晶体的基频．由式（4）可以推出，石英晶体谐振频率之差fp－fs＝Δf常小，这期间晶体呈电感性工作状态，它是决定振荡频率的重要因素．

图1中CMOS反相器和晶体构成科尔匹兹振荡电路．根据电路理论，振荡频率为

其中：

图中，Rd为阻尼电阻，其作用是降低环路增益，从而抑制CMOS反相器在高频下的寄生振荡，Rd的值可以用式（7）进行估算［10］

4 微质量的测试和分析

本实验采用的传感器是1块在20℃下实测频率为7．990 39 MHz的石英晶体切片，切割面经严格的光学抛光处理后，再在上下表面镀金膜，石英晶体夹在2片电极中间，形成如三明治式的结构，通过从膜上引出电极再封装外壳就构成了石英晶体传感器，如图2所示．

图2 石英晶体传感器外形

按照图1焊接电路，阻尼电阻Rd按式（7）计算选定，所得到的振荡波形如图3所示．

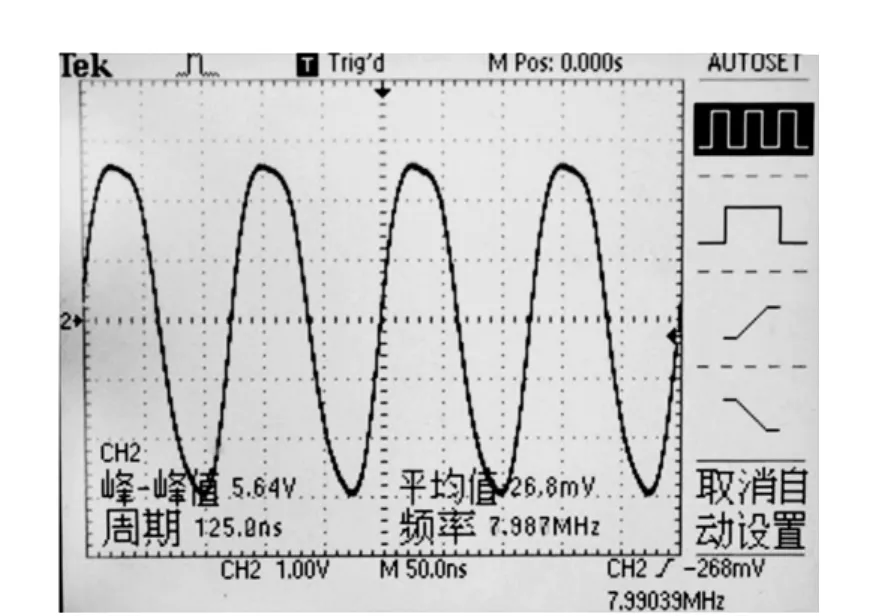
图3 振荡电路输出波形

利用该传感器进行微质量测量的过程如下：将细粉笔灰作为被测颗粒，在恒温设备中将其均匀地洒向传感器上方并让其自然下落，由于传感表面很小，因此可以近似地看作均匀地覆盖在晶体表面，待频率值稳定之后，记录覆盖前后测得的频率差值Δf，传感器接触表面的直径为7．52 mm，利用式（1）可以计算出质量变化Δm．

为了研究温度对晶体振荡频率的影响，在上一过程基础上，改变恒温设备的温度值，并记录电路振荡频率的变化情况，实验结果如表1所示．表1中，f0为不同温度下未覆盖颗粒时的振荡频率，f1为不同温度下覆盖颗粒后的振荡频率，Δf＝f1－f0，Δm为理论的颗粒质量．

表1 测量数据记录

由表1可以看出，测量出的细粉笔灰的理论质量是500 ng左右．但随着温度的升高，测量结果会发生变化，说明在采用晶体振荡进行微质量测量时，虽然晶体本身的温度漂移很小（本实验所用晶体实测温度相对漂移大约为8．75×10－6℃－1），但是由于测量灵敏度高，温度会对测量结果产生很大影响，因此，采用此方法进行微质量测量时，需要保持测量环境的温度恒定．

由于实验条件制约，本实验还存在一些不足之处，有待于进一步改进．主要体现为以下几点：

1）近似认为微小颗粒均匀的覆盖在电极的表面，实际分布的细微差别会带来误差．

2）缺乏更精确仪器对实验结果进行验证．

3）所用的数字示波器的频率测量精度有限，不能进行更精确的频率测量．