光伏电池输出电压的稳定性分析

侯世英，殷忠宁，罗书豪，张文玉

(重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆400044)

0 引言

在光伏系统中，由于光伏阵列具有非线性特征，并且其输出受太阳辐照度、环境温度影响较大，为了提高其效率，目前广泛采用的技术是最大功率点跟踪(maximum power point tracking，MPPT)[1－4]，而实现MPPT的关键是有效地控制光伏电池的输出电压或输出电流，但由于输出电压控制，相对于电流控制，具有更好的稳定性，且跟踪速度更快，因此，光伏电池的 MPPT控制，多采用电压控制方式[5－6]。

电压控制方式下光伏系统的MPPT控制模型如图1所示，光伏电池的输出电压由其输出端的DC/DC变换器进行控制，该DC/DC变换器采用的是输入端电压控制方式，即在输出端电压基本恒定的情况下，通过调节占空比来调节输入端电压[7－8]。

由于MPPT是一个动态追踪的过程，在追踪的过程中，光伏电池的输出电压会发生较大范围的波动，另外，由于光照强度、环境温度等条件的变化，光伏电池最大功率点处的电压也会在较大的范围内变化，从而导致DC/DC变换器的控制对象(光伏电池电压)，会发生较大波动。但是，光伏电池本身所呈现出的非线性的特性，很可能导致光伏系统的输出电压在不同的范围内呈现出不同的稳定性，较低的稳定性会给系统的运行带来非常不利的影响，因此，开展对光伏电池输出电压稳定性的研究显得很有必要。

针对上述问题，本文首先选取了两个比较典型的 DC/DC 变换器——Buck、Boost，对 MPPT 模式下光伏电池输出电压的稳定性进行了频域分析。针对光伏电池输出电压在采用Boost变换器进行控制时，所出现的不稳定现象，本文从改变Boost变换器拓扑的角度出发，对上述问题进行改进。为此，分别对Boost变换器的几种改进型拓扑——交错互联式Boost 变换器(interleaved Boost converter)[9]、三态Boost变换器(tri－ state Boost converter)[10]等进行研究，发现三态Boost变换器能够在光伏电池的宽输出电压范围内表现出良好的特性。最后，对上述结论进一步进行了时域仿真验证。

1 光伏变换系统的建模及分析

MPPT模式下光伏变换系统的控制模型如图1所示，光伏系统中控制光伏电池输出电压的DC/DC变换器有多种，本文选择了两种比较典型的变换器，即Buck和Boost变换器作为研究对象。对于系统数学模型的建立，本文采用状态空间平均法[11]。

图1 MPPT模式下光伏系统的控制模型Fig.1 Control model of PV system under MPPT mode

1.1 光伏电池的线性化模型

图2 给出了光伏电池的等效模型[12－14]。式(1)是与图2对应的光伏电池的 i－u特性方程[12]，其中Tc是电池内部绝对温度，uPV是光伏电池输出电压，Id0是二极管饱和电流，q是电子电荷，A是二极管系数，k是波尔兹曼常数，n是电池串联系数。

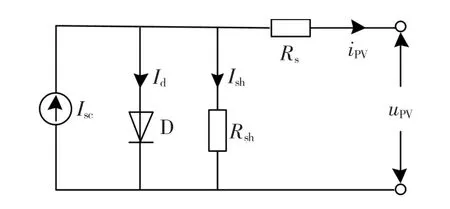
图2 光伏电池的等效电路Fig.2 The equivalent circuit photovoltaic cells

根据以上条件在仿真软件中搭建起光伏电池的仿真模型，图3分别给出了光伏电池的p－u及i－u特性曲线。

图3 光伏电池特性曲线Fig.3 The characteristic curve of PV cells

可以看出，光伏电池的输出呈现出明显的非线性的特性，为了建立光伏系统的数学模型，有必要将光伏电池进行线性化处理。本文采用的是切线化的方法[15]实现光伏电池的线性化。

i－u曲线在给定点(V，I)处的导数为

则光伏电池在给定点(V，I)处的线性化模型为

令Req=－1/k，Veq=V－I/k，则光伏电池的线性化等效电路如图4所示。

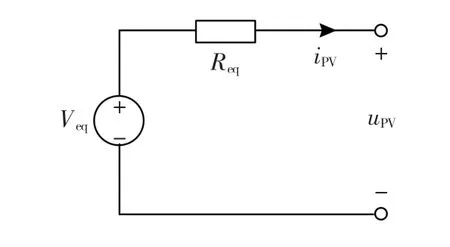
图4 光伏电池的线性化等效电路Fig.4 Linear equivalent circuit of PV cells

1.2 Buck降压模式下光伏系统的模型

图5 给出了带有线性光伏电池模型的Buck变换器，即MPPT模式下基于Buck变换器的光伏系统的等效电路。

图5 Buck降压模式下光伏系统模型Fig.5 The model of the PV system under Buck

应用状态空间平均法可得图5中电路的数学模型为

求解上式可得控制到输出的传递函数为

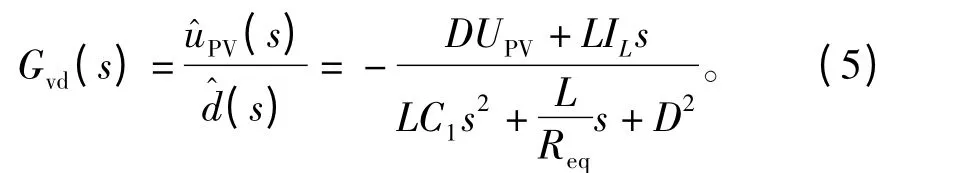
1.3 Boost升压模式下光伏系统的模型

图6给出了带有线性化光伏电池模型的Boost变换器，即MPPT控制模式下基于Boost变换器的光伏变换系统的等效电路。

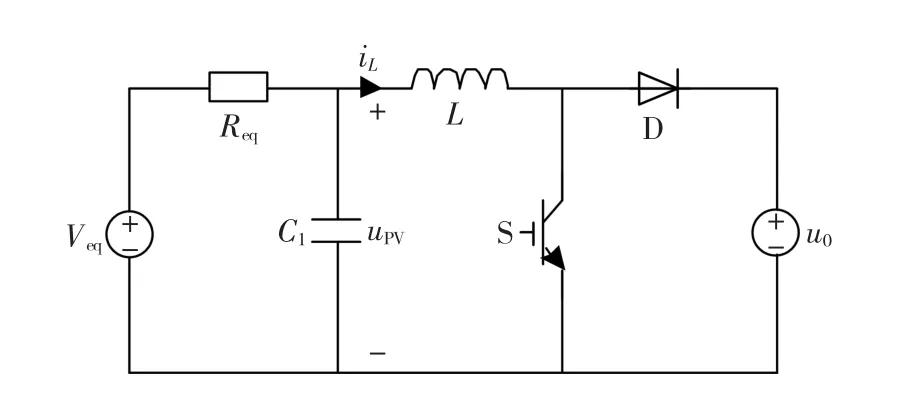
图6 Boost升压模式下光伏系统模型Fig.6 The model of the PV system under Boost

应用状态空间平均法可得图6中电路的数学模型为

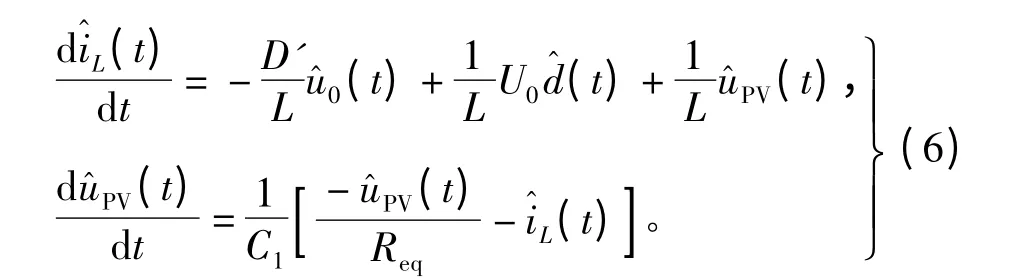
求解上式可得控制到输出的传递函数:

2 光伏电池输出电压稳定性的频率域分析

根据以上推导出的数学模型，本文依次选取了4个工作点对输入端电压控制模式下光伏电池输出电压的稳定性进行频率域内分析，如图3(b)中的a、b、c、d所示。在这4个工作点处分别绘制系统原始增益函数G0(s)所对应的Bode图。其中

图7为采用Buck变换器时，系统原始增益函数分别在 a、b、c、d等4个工作点处的 Bode图，可以看出，在从a到d的过程中，等效电阻Req的不断增大，并没有导致系统的相角裕度发生太大变化，系统的相角裕度一直保持在90°左右，系统的稳定性受工作点的影响很小。

图7 采用Buck变换器时系统的Bode图Fig.7 Bode plots of the system under Buck converter

图8 为采用Boost变换器时，系统分别在 a、b、c、d等4个工作点处的 Bode图，在从 a到 d的过程中，导致系统的稳定裕度不断降低，系统的相角裕度由a点处的74.5°，最终降到了d点处的0.785°，系统的稳定性受到了很大影响，这对系统的运行是很不利的。

图8 采用Boost变换器时系统的Bode图Fig.8 Bode plots of the system under Boost converter

3 三态Boost变换器在光伏系统中的应用

三态 Boost变换器最早由 Viswanathan K[16]提出，最初设计的目的是消除传统Boost变换器存在的非最小相位系统，其结构图如图9所示。

图9 三态Boost变换器Fig.9 Tri-state Boost converter

根据开关管Sf、Sm以及二极管D2的不同导通组合，稳态时，不同于传统变换器的两种工作状态，这种新型变换器存在3种工作状态，分别如图10所示。

图10 三态Boost变换器的3种工作状态Fig.10 The three modes of tri-state Boost converter

各种状态下的占空比有如下约束关系

亦即可通过任意控制其中的两个独立变量便控制电路的状态。

3.1 三态Boost升压模式下光伏系统模型

图11给出了带有线性化光伏电池模型的三态Boost变换器，即输入端电压控制模式下三态Boost光伏变换系统的等效电路。

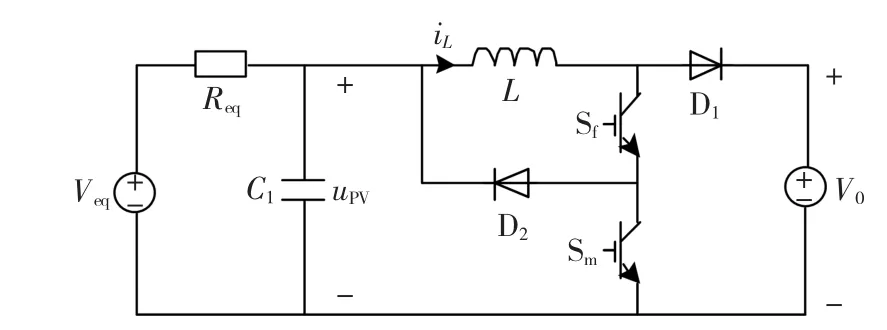
图11 三态Boost升压模式下的光伏系统模型Fig.11 The model of the PV system under Tri-state Boost converter

应用状态空间平均法可得图11中电路的数学模型为

求解上式可得控制到输出的传递函数为

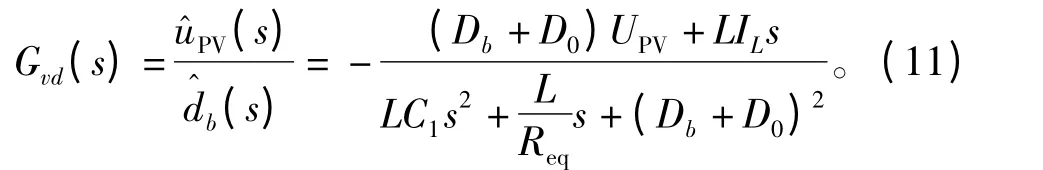
3.2 频率分析

此处，同样选取了与第3节中相同的4个工作点对采用三态Boost变换器时光伏电池输出电压的稳定性进行频域内分析。在该4个工作点处分别绘制系统原始增益函数G0(s)所对应的Bode图，如图12所示。

图12 采用三态Boost变换器时系统在各个工作点处的Bode图Fig.12 Bode plots in each operating points of the system under tri-state Boost converter

由图12可以看出，在从a到d的过程中，等效电阻Req的不断增大，系统的相角裕度并没有像Boost变换器一样发生很大变化，而是表现出了像Buck变换器一样的特性，一直保持在90°左右，系统的稳定性受工作点影响很小。

4 光伏电池电压稳定性的时域分析

为了进一步验证上述分析结果的正确性，本文在PSIM6.0中搭建了MPPT模式下光伏系统的仿真模型，光伏电池的p－u及 i－u特性曲线如图3所示。仿真中采用扰动观察法，采样频率为50 Hz，步长 Δu=0.2 V。

4.1 Buck降压模式下的时域分析

采用Buck变换器时，其输出端电压设定在6 V。图13中给出了光伏电池输出电压初始值 uPV－set分别设定在光伏电池的电流源区和电压源区时，光伏电池在MPPT模式下实际输出电压的波形，可以看出，不论uPV－set在光伏电池的电流源区还是电压源区内，光伏电池的实际输出电压波形都具有较好的稳定性。

图13 采用Buck变换器时光伏电池输出电压波形Fig.13 The waveforms of output-voltage of the PV cells under Buck converter

4.2 Boost升压模式下的时域分析

采用Boost变换器时，其输出端电压设定在30 V。图14(a)、图14(b)中给出了光伏电池输出电压的初始值uPV－set分别设定在光伏电池的电流源区和电压源区时，光伏电池在MPPT模式下实际输出电压的波形。可以看出，uPV－set在光伏电池的电流源区时，光伏电池输出电压的稳定性是比较差的，并且uPV－set的值越小，实际输出波形越差;而 uPV－set在光伏电池的电压源区时，光伏电池实际输出电压的稳定性相对较好，但其稳定性受工作点的影响依然是比较明显的。

图14 采用Boost变换器时光伏电池输出电压波形Fig.14 The waveforms of output-voltage of the PV cells under Boost converter

4.3 三态Boost升压模式下的时域分析

采用三态Boost变换器时，其输出端电压的设定值同样为30 V。图15中给出了光伏电池输出电压的初始值uPV－set分别设定在光伏电池的电流源区和电压源区时，光伏电池在MPPT模式下实际输出电压的波形。可以看出，uPV－set无论是在光伏电池的电流源区还是电压源区，光伏电池的实际输出电压的稳定性都是比较好的。可以看出，与传统的Boost变换器相比，三态Boost变换器有效拓宽了光伏电池输出稳定电压的范围，且具有更好的动态响应特性。

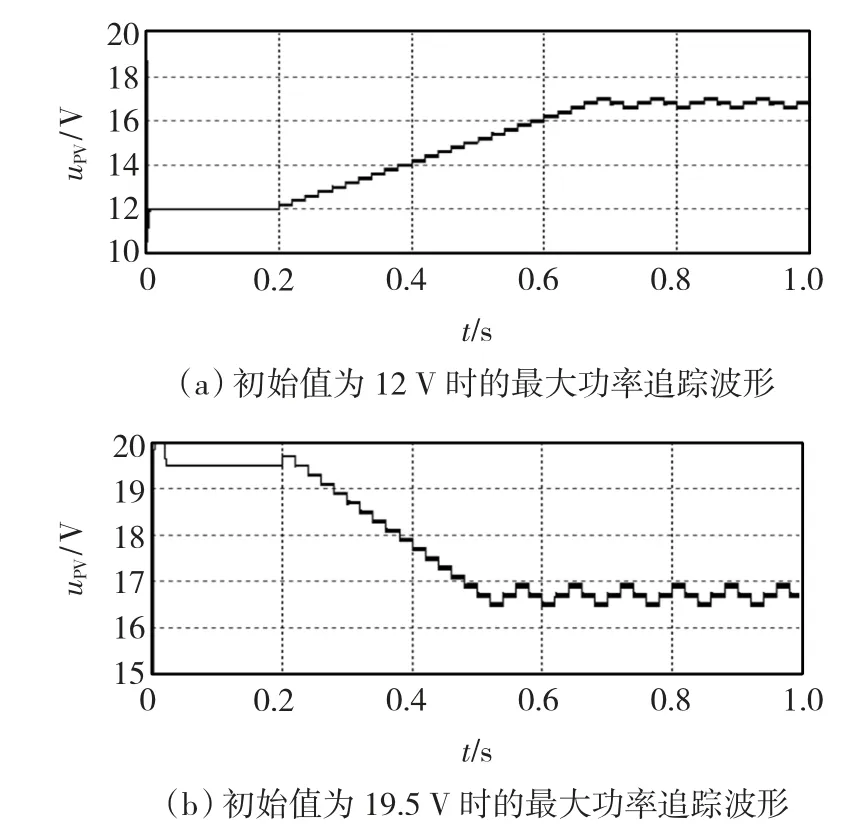
图15 采用三态Boost变换器时光伏电池电压波形Fig.15 The waveforms of output-voltage of the PV cells under tri-state Boost converter

5 结语

本文对光伏电池输出电压的稳定性进行了分析，通过建立系统的数学模型并搭建相应的仿真模型，分别在频率域内和时域内对系统在不同工作点处的稳定性进行了分析。最后，针对传统的 Boost变换器在光伏电池的宽电压输出范围内，难以维持稳定的输出的特性，本文所提出的采用三态 Boost变换器代替传统的Boost变换器来进行光伏电池输出电压的控制的方法，有效地拓宽了光伏电池输出稳定电压的范围，对提高独立光伏系统的稳定性和可靠性具有非常重要的实用意义。

[1]HOHM D，ROPP M.Comparative study of maximum power point tracking algorithms[J].Progress in Photovoltaics，2003，11(1):47－62.

[2]SALAS V，OLIAS E，BARRADO A.Review of the maximum power point tracking algorithms for stand-alone photovoltaic systems[J].Solar Energy Materials and Solar Cells，2006，98(11):1555－1578.

[3]MAHESHAPPA H D，NAGARAJU J，MURTHY M V.An improved maximum power point tracker using a step－up converter with current locked loop[J].Renew Energy，1998，13(2):195－201.

[4]FEMIA N，PETRONE G，SPAGNUOLO G.Optimization of perturb and observe maximum power point tracking method[J].IEEE Transactions on Power Electronics，2005，20(4):963 －973.

[5]XIAO Weidong，DUNFORD W G，PALMER P R，et al.Regulation of photovoltaic voltage[J].IEEE Transactions on Industrial Electronics，2007，54(3):1365 －1374.

[6]BRUNTON S L，ROWLEY C W，KULKARNI S R，et al.Maximum power point tracking for photovoltaic optimization using ripple-based extremum seeking control[J].IEEE Transactions on Power Electronics，2010，25(10):2531－2540.

[7]罗明，杨金明.双级式光伏系统最大功率点跟踪研究[J].电力电子技术，2009，43(5):20 －21.LUO Ming，YANG Jinming.Research on MPPT of the double stage PV system[J].Power Electronics，2009，43(5):20 －21.

[8]程军照，吴夕科，李澍森，等.采用Boost的两级式光伏发电并网逆变系统[J].高电压技术，2009，35(8):2048－2052.CHENG Junzhao，WU Xike，LI Shusen，et al.Boost-based twolevel grid-connected photovoltaic inverter system[J].High Voltage Engineering，2009，35(8):2048－2052.

[9]BROECK H，TEZCAN I.1 kW dual interleaved boost converter for low voltage applications[C]//CES/IEEE 5th International Power Electronics and Motion Control Conference，August，14 －16，2006，Shanghai，China.2006:1551 － 1555.

[10]刘兆娟，刘锦波.基于输入输出反馈线性化三态Boost DC/DC变换器的新型控制策略[J].山东大学学报:工学版，2008，38(1):43 －47.LIU Zhaojuan，LIU Jinbo.A new control strategy of a tri-state Boost DC/DC converter based on input-output linearization[J].Journal of Shandong University:Engineering Science，2008，38(1):43－47.

[11]陈亚爱.开关变换器的实用仿真与测试技术[M].北京:机械工业出版社，2009.

[12]任碧莹，钟彦儒，孙向东，等.基于 PSIM软件的光伏电池特性的仿真建模研究[J].西安理工大学学报，2007，23(4):257－260.REN Bixia，ZHONG Yanru，SUN Xiangdong，et al.Simulation modeling of characteristics of PV cells based on PSIM software[J].Journal of Xi＇an University of Technology，2007，23(4):257－260.

[13]李春华，朱新坚，胡万起，等.光伏/燃料电池联合发电系统的建模和性能分析[J].电网技术，2009，33(12):88－93.LI Chunhua，ZHU Xinjian，HU Wanqi，et al.Modeling and performance analysis of photovoltaic/fuel cell hybrid power generation systems[J].Power System Technology，2009，33(12):88－93.

[14]茆美琴，余世杰，苏建徽.带有MPPT功能的光伏阵Matlab通用仿真模型[J].系统仿真学报，2005，17(5):1248 －1251.MAO Meiqin，YU Shijie，SU Jianhui.Versatile Matlab simulation model for photovoltaic array with MPPT function[J].Journal of System Simulation，2005，17(5):1248 －1251.

[15]VILLALVA M G，SIQUEIRA T G，RUPPERT E.Voltage regulation of photovoltaic arrays:small-signal analysis and control design[J].IET Power Electronics，2010，3(6):869 － 880.

[16]VISWANATHAN K，ORUGANTI R，SRINIVASAN D.A novel tri-state boost converter with fast dynamics[J].IEEE Transactions on Power Electronics，2002，17(5):677 －683.