考虑弧垂的交流特高压输电线三维电磁场

兰生，张振兴，原永滨

(福州大学 电气工程与自动化学院，福建 福州350108)

0 引言

随着社会经济的快速发展，用户对电能的需求越来越大，加之我国能源分布的不平衡，需要加快建设特高压输电网[1]。特高压输电可能够实现大容量、远距离输电，降低损耗，节省线路走廊，有利于构建坚强电网[2]。我国的特高压交流输电额定电压等级为750 kV和1 000 kV，是目前国内最高电压等级[3]。目前，中国正在运行的特高压交流输电线路示范工程，即晋东南—南阳—荆门1 000 kV特高压交流输电，为最新应用。对特高压输电线路的电磁环境进行的一些研究，主要包括工频电场、工频磁场、无线电干扰和可听噪声等理论以及试验研究，并取得了一系列成果。特高压输电线路工频电磁场对其附近的人和生态是否会带来危害，一直以来都是大众十分关心的问题。通过特高压试验线路或正在运行的超高压线路进行电磁测量和生物效应研究，作为主要依据来制定电磁环境限值。线路产生的电磁场已经成为输电工程中关键的影响因素[4]。因此，电磁场的数值计算成为特高压输电的一个关键技术。工程电磁场数值计算方法，主要包括有限元法以及逐次镜像法、模拟电荷法、矩量法等[5]。文献[3]提出了基于有限元法建立模型，计算分析了特高压紧凑型输电线路附近场强以及导线表面场强。文献[6]采用了逐次镜像法计算特高压输电线路各种塔型导线下方电场强度和导线表面场强。文献[7]利用复镜像理论计算了特高压输电线路工频磁场，但是求解误差受到镜像次数影响，如果导线间的最小距离与导线半径比值越大，镜像次数越少，那么误差会变大。文献[8]采用了模拟电荷法，通过Matlab仿真实现了超高压输电线路周围电磁场计算，在精确度上存在较大误差。文献[9]利用有限元—有界元法，进行电磁场开域求解。有限元法作为一种求解边界问题方法，已经有很多成熟应用的有限元软件，能够灵活选择网格剖分精确度。目前，利用有限元法计算特高压输电线路下方电磁场，大多是把输电线路等效为直导线模型。本文针对特高压输电线路的实际线路的弧垂情况，进行电磁有限元仿真，使计算结果更加接近真实值。

1 电磁场计算理论

由于架空输电线路产生的工频电磁场满足，周围场点到导线的距离远小于相应的时谐电场在空气中的波长，可以近似为准静态场。故可类比地采用静态电磁场的分析方法与结论进行相应的分析与计算。因此可以得到电准静态场所满足的麦克斯韦方程，即

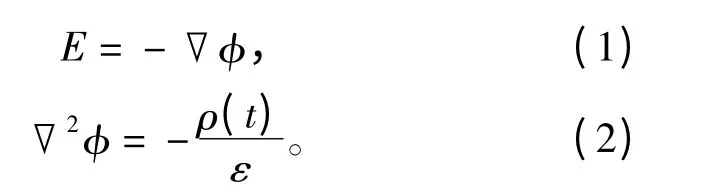
同理，磁准静态场也满足

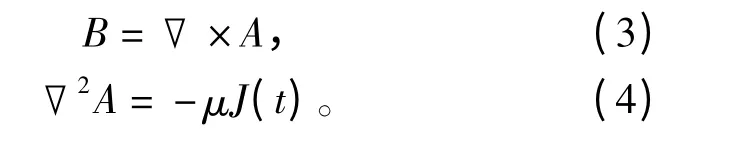
式中，μ和ε分别为介质的磁导率和介电常数，B和A分别表示磁通密度和矢量磁位。∇2为拉普拉斯算子，即

狄利克莱边界条件表示为

式中:Γ为狄利克莱边界;g(Γ)是位置的函数，可以是常数或者零。

诺依曼边界条件可表示为

式中:Γ为诺依曼边界;n为边界Γ的外法线矢量;f(Γ)和h(Γ)为一般函数(可为常数或零)，当为零时为奇次诺依曼条件。

由于在电磁场微分方程的求解中，只有边界条件和初始条件限制，方程才能有定解，故需要设置边值和初值。

在磁场有限元分析中，当场是作正弦变化且频率较低时，准静态磁场可用时谐场来求解。本文计算的是实际交流特高压输电线路周围磁场分布，故可采用时谐磁场进行计算。

以磁感应强度为例，b(r，t)可由复数函数的实部表达为

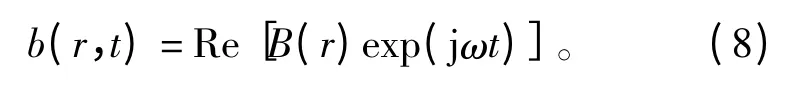
其中:

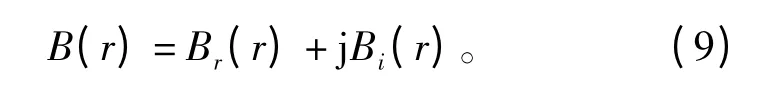
上式中，Re[]为复数实部记号。Br(r)和Bi(r)分别对应B(r)的实部和虚部，B只有空间坐标决定。

2 电磁场仿真

2.1 线路基本数据

交流特高压输电线路额定电压为1 000 kV，最高运行电压1 100 kV，额定相电流4 000 A。杆塔结构为酒杯型，如图1所示。单回三相导线水平I－V－I排列，相间距离为22.2 m;杆塔顶端两侧装设避雷线，两根架空地线相距46 m，距导线垂直距离22.33 m。三相子导线选择钢心铝绞线，型号为ACSR－720/50，每相采用对称八分裂导线，分裂间距为40 cm。架空地线选择光纤复合铝包钢绞线(OPGW)，导线规格为500 mm2，导线分裂根数为2根。在计及悬链线时，取档距 L=400 m，由文献[10]弧垂计算公式，可得弧垂高度s=10.24 m。

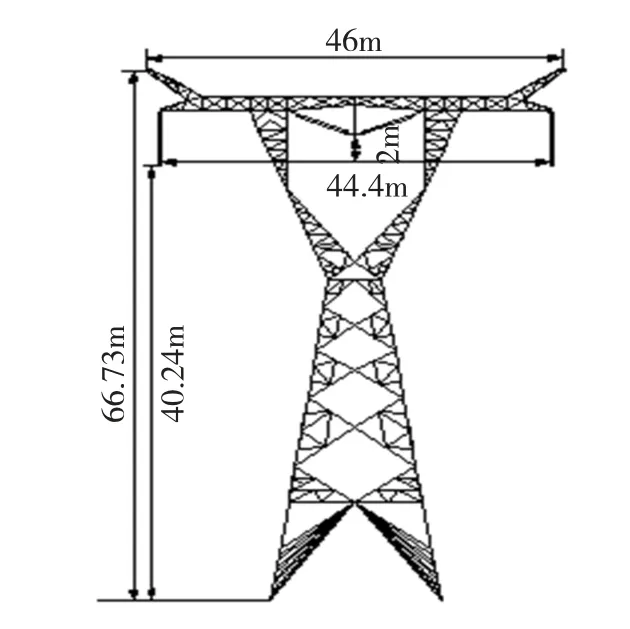
图1 酒杯塔Fig.1 Glass tower

2.2 三维电磁场建模

由于实际特高压输电线路比较复杂，而且有些因素的影响可以忽略不计，因此有必要对实际线路进行合理地简化。本文对输电线路三维模型作如下简化[11]:

1)地面是无穷大导体，电位为零，沿线地面电阻率相同;

2)输电导线分别用长直导线和悬链线代替而且同一档距内的同型导线具有相同等效半径且彼此平行，导线表面等电位，导线为等磁位面;

3)只考虑线路主要部分形成的电磁场，忽略杆塔、金具、绝缘子等附近物体的影响，不考虑导线、架空地线的端部效应;

4)认为电荷分布沿线路分布没有畸变，不考虑线路上电位的变化;

5)假设线路电流为正弦稳态电流，并沿导线轴线流动。

通过简化，分裂导线建模时采用文献[12]中的等效半径计算式(10)，求出相导线的等效半径。

式中:m为分裂根数;r为子导线半径，单位m;R为分裂导线外接圆半径，单位m。

模型建立时，以档距中央为坐标原点。电场建模时，对于长直导线模型，导线对地高度取最大弧垂处的高度。边界和地面围成的半径120 m，长度400 m的上半圆柱体为空气域，其底面圆心坐标为(－200，0，0)，与地面、导线组成求解区域。对于磁场，需加上大地区域，大小与空气区域一样。特高压输电线路计算三维模型如图2所示。

图2 三维模型Fig.2 3D model

2.3 模型求解

电场计算时，边界电位取为零。电压采用额定运行电压的105%，即1 050 kV。由于每一时刻下得到的电场强度是瞬时值，又导线表面电场线方向垂直于导线表面。因此，电场求解时候，可按A相初始相角为0°和90°分别施加电压载荷，取求解点2次计算结果的均方根，得到该点电场强度的有效值[13]。地面上电场水平分量近似为0，可认为近似垂直地面，那么这种计算方法可用于地面电场求解。

对于准静态磁场求解，采用的是谐波场的分析方法。需对磁场的外边界施加磁力线平行条件。电流载荷分成实部和虚部加载，分别得到磁场的实部和虚部求解值，再将两者合成，得到磁场的有效值。

3 工频电场仿真结果与分析

3.1 长直导线模型三维电场仿真结果

采用简化的长直导线计算模型，通过ANSYS仿真后，将地面上方1.5 m档距中央(x=0)投影处的两次电场强度导出。利用Excel，以离线路中心距离为x轴，电场强度为y轴，得到导线下方地面上工频电场横向分布，如图3所示:

由图3，可总结出线路下方地面上工频电场横向分布规律:电场关于线路中心对称，电场最大值出现在两边相外侧附近，线路中心投影点两侧分别沿轴线正反方向衰减，衰减到边相附近开始增大直至最大值，随着距边相投影点距离增大，电场强度衰减很快。

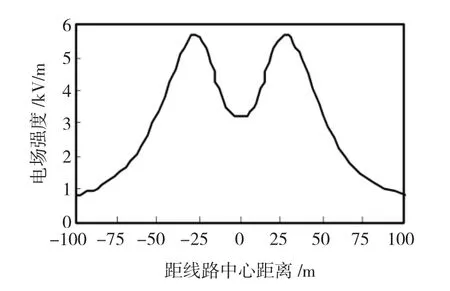
图3 长直导线工频电场横向分布(y=1.5)Fig.3 Rectilinear conductor model(y=1.5)

3.2 考虑导线弧垂三维电场仿真结果

同理，利用 ANSYS仿真后，分别选取 x=0 m、x=100 m、x=200 m 3个截面，得到其工频电场横向分布，如图4所示。

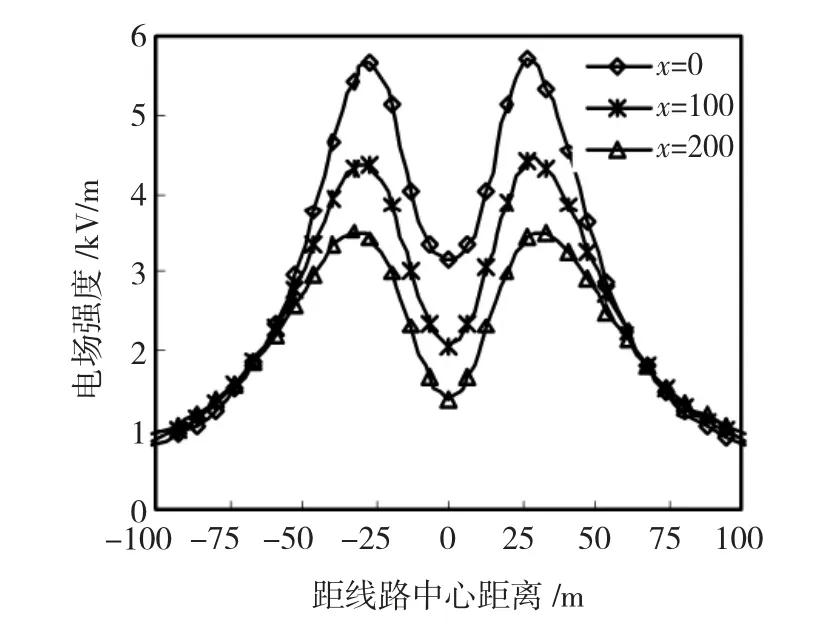
图4 考虑导线弧垂工频电场横向分布(y=1.5)Fig.4 Considering sag model(y=1.5)

图4 可反映出电场分布的横向和纵向特征，仿真所得电场分布呈轴对称形:沿横向，电场分布出现两个峰值，位于边相外侧投影附近;沿纵向，朝导线轴向衰减，电场强度最大值出现在输电线路的弧垂最大处，杆塔处场强最小。

3.3 两种三维模型的仿真结果比较分析

将图3与图4比较，可以得出以下几点:

1)长直导线模型能反映出输电线路电场的横向分布特征。

2)三维模型能够同时反映输电线路下方电场的横向与纵向分布特征。沿纵向，朝两侧方向衰减，电场强度最大值出现在输电线路的弧垂最大处，杆塔处场强最小。

3)两种模型在弧垂处数值一样。离档距中心越远，两种计算模型所得的电场值差别越大。

说明考虑导线弧垂的三维模型更为准确，能够更为细致地反映线下电场的分布规律。

3.4 仿真结果与实测值对比分析

文献[14]在特高压交流试验示范工程试运行期间，所测得的农田区域导线最大弧垂处电场横向分布如图5所示。与本文最大弧垂处下方电场强度的计算结果对比，两者的横向分布特征一致，数值略微偏小。本文计算得到的特高压线路下方场强最大值接近6 kV/m，根据现有我国特高压输电线路工频电场制定的限值，仍然符合要求。

图5 特高压输电线路下方工频电场横向分布Fig.5 Transverse distribution of the electric field under UHV AC transmission line

4 工频磁场的计算结果

4.1 长直导线模型三维磁场的计算结果

采用简化的长直导线计算模型，通过计算后，得到线路下方工频磁场实部分量、虚部分量、合成分量的横向分布，如图6所示。

图6 长直导线工频磁场横向分布(y=1.5)Fig.6 Rectilinear conductor model(y=1.5)

从图6可以看出，磁感应强度的实部、虚部分布呈不对称分布，这是由于三相导线电流的实部或虚部不可能一样，因此产生的磁场叠加后也不对称。合成磁感应强度关于线路中心对称，其最大值符合我国特高压输电线路工频磁场限值要求。工频磁场分布规律:磁感应强度最大值出现在线路中心，在三相导线投影范围内，磁感应强度变化很小，在边相导线投影外侧，磁感应强度明显降低。

4.2 考虑导线弧垂三维磁场仿真结果

通过计算后，为了分析考虑导线弧垂模型时，地面上方工频磁场的变化情况，分别选取x=0 m、x=100 m、x=200 m 3个截面，得到其工频磁场横向分布，如图7所示。

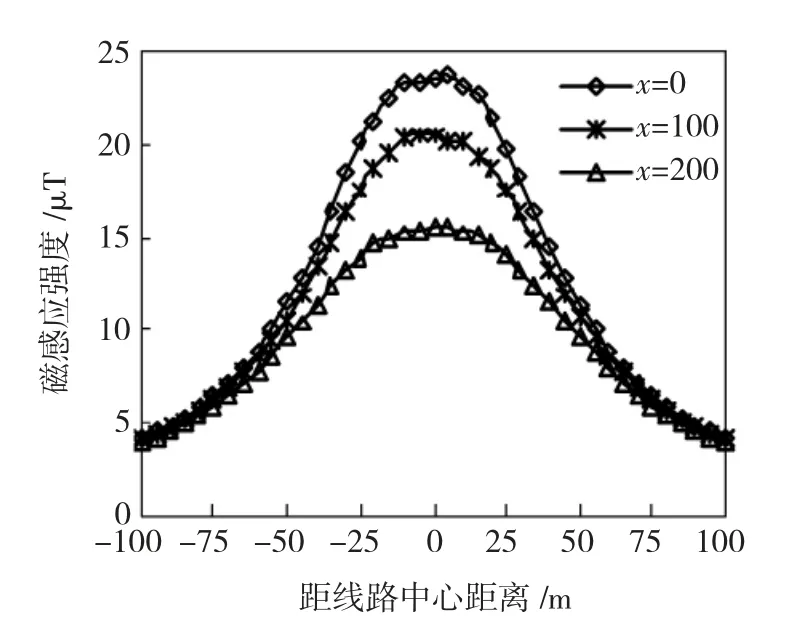
图7 考虑导线弧垂工频磁场横向分布(y=1.5)Fig.7 Considering sag model(y=1.5)

图7 反映出线路下方工频磁场分布的横向和纵向特征，磁场分布关于线路中心对称:沿横向，磁感应强度峰值出现在线路中心;沿纵向，朝导线轴向衰减，磁感应强度最大值出现在输电线路的弧垂最大处，杆塔处磁感应强度最小。

4.3 两种三维模型仿真结果比较分析

将图6与图7比较，可以总结出长直导线三维模型与考虑导线弧垂三维模型磁场计算结果的异同点:

1)长直导线维模型仅仅能反映出输电线路磁场横向变化特点:关于线路中心对称。

2)考虑导线弧垂三维模型能够同时反映输电线路下方磁场的横向与纵向变化特点，计算所得磁场分布呈轴对称。沿线路纵向磁感应强度最大值出现在输电线路弧垂最大处，并且朝两侧方向衰减，杆塔处的磁感应强度最小。

3)在弧垂处，两种模型计算的磁感应强度一致。

5 结论

本文通过有限元法，对线路模型进行简化后、直观地仿真分析了特高压输电线路的电磁场。考虑导线弧垂的三维模型能够同时反映输电线路下方电磁场的横向与纵向变化特点，计算所得场强分布呈轴对称形。沿线路纵向电磁强度最大值出现在输电线路最大弧垂处，并且朝两侧方向衰减，杆塔处的电磁强度最小。考虑导线弧垂的三维模型能够更加完整地分析空间中导线周围电磁场，计算结果更加准确。

[1]邬雄，万保权，路遥.1000kV级交流输电线路电磁环境的研究[J].高电压技术，2006，32(12):55 －58.WU Xiong，WAN Baoquan，LU Yao.Study on electromagnetic environment for 1000kV AC transmission line[J].High Voltage Engineering，2006，32(12):55 －58.

[2]黄道春，阮江军，余世峰，等.特高压紧凑型输电线路工频电场强度计算[J].高电压技术，2006，32(7):69 －71.HUANG Daochun，RUAN Jianjun，YU Shifeng，et al.Calculation of the power frequency eletric field intensity of UHV compact transmission lines[J].High Voltage Engineering，2006，32(7):69－71.

[3]刘振亚.特高压电网[M].北京:中国经济出版社，2005.

[4]张利庭，胡白雪，周浩.特高压输电线路下方工频电磁场的研究[J].能源工程，2006(4):49 －53.ZHANG Liting，HU Baixue，ZHOU Hao.Study on the power frequency electromagnetic field under UHV transmission lines[J].Energy Engineering，2006(4):49 －53.

[5]倪光正，杨仕友，钱秀英，等.工程电磁场数值计算(M).北京:机械工业出版社，2004.

[6]黄道春，阮江军，文武，等.特高压交流输电线路电磁环境研究[J].电网技术，2007，31(1):6 －11.HUANG Daochun，RUAN Jianjun，WEN Wu，et al.Study on electromagnetic environment of UHV AC transmission lines[J].Power System Technology，2007，31(1):6 － 11.

[7]牛林，赵建国，李可军.1000kV特高压交流输电线路工频磁场分析[J].山东大学学报:工学版，2010，40(1):154 －158.NIU Lin，ZHAO Jianguo，LI Ke jun.Study of a power frequency magnetic field of 1000 kV UHV AC transmission lines[J].Journal of Shang Dong University:Engineering Science，2010，40(1):154－158.

[8]WANG Fei，WANG Weijie，JIANG Zhichao.Analysis of the Linefrequency Electric Field Intensity around EHV Transmission[C]//2010 International Conference on Electrical and Control Engineering，June 26 －28，2010，Wuhan，China.2010:3344 － 3346.

[9]高俊吉，刘大明.边界棱棱边元 FEM－BEM法在开域静磁场计算中的应用[J].哈尔滨工程大学学报，2009，30(11):1311－1316.GAO Junji，LIU Daming.Application of an FEM-BEM method based on boundary edge elements to open boundary magnetostatic problems[J].Journal of Harbin Engineering University，2009，30(11):1311－1316.

[10]肖冬萍，何为，张占龙，等.特高压输电线工频磁场三维优化模型[J].中国电机工程学报，2009，29(12):116 －120.XIAO Dongping，HE Wei，ZHANG Zhanlong，et al.Three-dimension optimization model for power frequency magnetic field of UHV transmission lines[J].Proceedings of the CSEE，2009，29(12):116－120.

[11]Maruvada P.Sarama，Jainschewskyj.Electrostatic field of a system of parallel cylindrical conductors[J].IEEE Transactions on Power Apparatus and Systems，1969，88(7):1069 － 1078.

[12]牛林，杜至刚，赵建国.1000kV级交流特高压输电线路导线做小对地距离研究[J].电力自动化设备.2008，28(1):17－22.NIU Lin，DU Zhigang，ZHAO Jianguo.Bundle conductor minimum ground clearance of 1000kV AC UHV transmission lines[J].Electric Power Automation Equipment.2008，28(1):17－22.

[13]张宇，郑伟，文武，阮江军，等.架空线路分裂导线表面电位梯度的数值计算[J].高电压技术，2005，31(1):23 －25.ZHANG Yu，ZHENG Wei，WEN Wu，et al.Numerical calculation of electric field intensity on the surface of bundle conductors of overhead transmission lines[J].High Voltage Engineering，2005，31(1):23 －25.

[14]刘振亚.特高压交流输电技术研究成果专辑(2008年)[M].北京:中国电力出版社，2009.