基于复杂度和符号空间的离心泵空化状态估计

宋向荣，李建康

(1.江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003;2.江苏大学 理学院，江苏 镇江 212013)

基于复杂度和符号空间的离心泵空化状态估计

宋向荣1，李建康2

(1.江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003;2.江苏大学 理学院，江苏 镇江 212013)

对结构多个测点的振动响应序列，利用多值粗粒化方法转化为符号序列，进行Lempel-Ziv复杂度分析，构建描述结构的动力学特性符号空间。以某离心泵为例，利用符号空间方法对该泵空化状态进行估计，与工作模态分析方法对比验证了结论。为难以准确建模的复杂结构和复杂环境的状态估计提供一种新方法。

Lempel-Ziv复杂度;符号空间;离心泵;空化与空蚀;状态估计

泵的空化过程是由于泵内液体在低压区形成气泡并发展、溃灭的过程。空化过程中，气泡经过泵内高压区时，急速收缩溃灭，在液体中形成激波或高速微射流，引起泵体剥蚀，是泵的一种主要破坏形式。该过程中通常伴随很强的振动和水动力噪声［1］。研究泵的空蚀状态估计对泵的合理设计以及提高综合性能具有重要的意义。

振动和噪声测试分析是研究泵空化和空蚀特性的重要手段之一。但由于空化过程的非线性特性，以线性模型为基础的模态识别和传递函数分析等手段，虽然对结构振动分析比较适合，但对空化状态估计显得略有不足。本文应用Lempel-Ziv复杂度和符号空间方法，利用泵振动响应进行空化状态估计。

1 结构状态估计的符号空间构建

结合Lempel-Ziv复杂度的符号方法在医学、信号处理、图形学等领域已经广泛应用［2～5］，但在结构振动响应分析领域应用较少［6］。结构响应是环境或载荷作用下的结构动力学特性反映，其本质是一种时间序列，通过对振动响应序列的Lempel-Ziv复杂性度量，可以在符号空间内描述结构的振动特性。

首先将振动响应时间序列转变为符号序列，本文采用多值粗粒化方法［7］来重构振动时间序列。设已知的时间序列为x1，x2，…，xn，求出该时间序列的最大值和最小值。定义字符集A={0，1，…，α－1}，产生的符号序列由下式定义

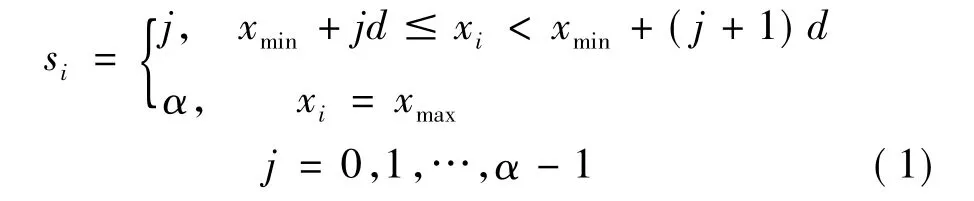
即定义了映射si=f(xi)，将时间序列 x1，x2，…，xn转变为符号序列 s1，s2，…，sn，其中 si∈A。

设所描述的系统具有N个自由度。由振动理论可知，系统任一点的响应可表示为N阶模态响应的线性组合，由各阶模态向量组成N×N阶模态矩阵反映了系统的结构特性。本文利用Lempel-Ziv复杂度分析构建符号空间来描述结构动力学状态。

设第i个响应点测得的序列，经符号化后得到一个符号串:

Lempel-Ziv复杂度由添加和复制2种操作实现［8］，广泛应用于非线性科学的研究中。设上述符号序列的Lempel-Ziv复杂度为mi，则复杂度计算过程中将产生一系列新符号S'i，这些新符号是Si的子串，共有 mi个。以xik表示S'i在Si中出现的次数，即复制数。则第i个响应点状态的描述可由下式表示:

这里，S'ik这里作为符号空间的基，因此用黑体表示。根据符号动力学的相空间重构方法，结构任一点的响应序列均能产生一个mi维的符号空间。设产生的新符号S'ik，有n个相互独立的，记为S'j，于是第i个响应点的状态可描述为:

这样，我们就用一个n维的符号空间来描述整个振动系统的动力特性。其中，

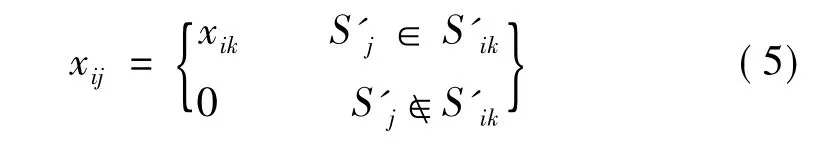
表示n维符号空间对应符号的权系数，或符号空间的坐标。

由响应序列产生的符号空间的维数n即整个系统的复杂度，n越大系统越复杂，n越小反映系统越有规律。这里与传统的模态空间分析不同的是，物理空间与模态空间的转换矩阵来自振动系统质量矩阵和刚度矩阵;而我们这里物理空间与符号空间的转换矩阵来自振动系统的各点响应。由此看出，基于符号空间的系数矩阵在物理意义上与模态空间的转换矩阵相似。符号空间的基是由系统响应序列经LZ复杂度计算产生的一系列新符号，权系数反映了这些新符号参与结构动态特性响应的贡献量，则权系数矩阵反映了结构的动力学特性，通过对该矩阵的分析可以描述系统的状态。对系统的动力学整体状态的准确描述有助于对结构的控制、动力学参数修改、动力学设计等。

2 离心泵空化状态估计

由于泵空化汽泡溃裂的激振，以及汽泡对泵体的冲击，常引起泵体振动伴随噪声。振动和噪声测试是泵空化和空蚀诊断的一种重要方法，测试方法简单直接，效果明显。通过振动和噪声对比分析可以判断出泵的汽蚀水平。为研究离心泵的动力学特性，需要测试不同流量和进口压力下的泵加速度响应和噪声，以及研究空蚀点附近泵的特性的变化。

本文以某船用离心泵为例，测试了该泵在不同流量，不同进口压力下各测点的加速度响应和泵壳体附近的噪声。测试系统采用LMS振动噪声测试与分析系统，传感器为PCB公司的ICP型加速度传感器、ICP型麦克风。软件系统采用与硬件系统紧密集成的LMS Test.lab软件的Signature Acquisition模块。主要振动测点有基脚，进口，出口，蜗壳，轴承，电机等，共计11个测点，18个通道(部分测点布置的是3向加速度传感器)，并同时测量蜗壳附近噪声。部分测点布置见图1。

振动测试采用固定采样频率时间跟踪，采样频率25 600 Hz，频率分辨率 0.5 Hz，分析频率 8 000 Hz。噪声分析频率10 240 Hz，频率分辨率1.56 Hz。为便于对比，取某一流量下2种进口压力工况的各测点响应进行分析。

图1 离心泵测点布置Fig.1 Sensor location

图2(a)为不发生空化时蜗壳测点的加速度响应云图，该图是三维彩图，其横坐标为频率，纵坐标为时间，颜色表示振动加速度大小。改变进口压力，使泵发生较严重汽蚀时，图2(b)为严重空化时蜗壳测点的加速度响应云图，此时振动明显加剧，高频成分变得复杂。从2个工况下对应声压测点频谱特性分析也可以看出，空化时泵的整体噪声水平变高，高频振动部分增强更为明显。说明振动测试方法可用于泵的空化现象的辨识，但频谱图分析仅提供的直观印象，没有具体数值的比较，或者说关于汽蚀描述的参数问题，以及除了响应大小、振动强弱等指标外，如何描述泵的整体动态特征水平问题，是解决泵的空化和空蚀问题的一个关键手段。

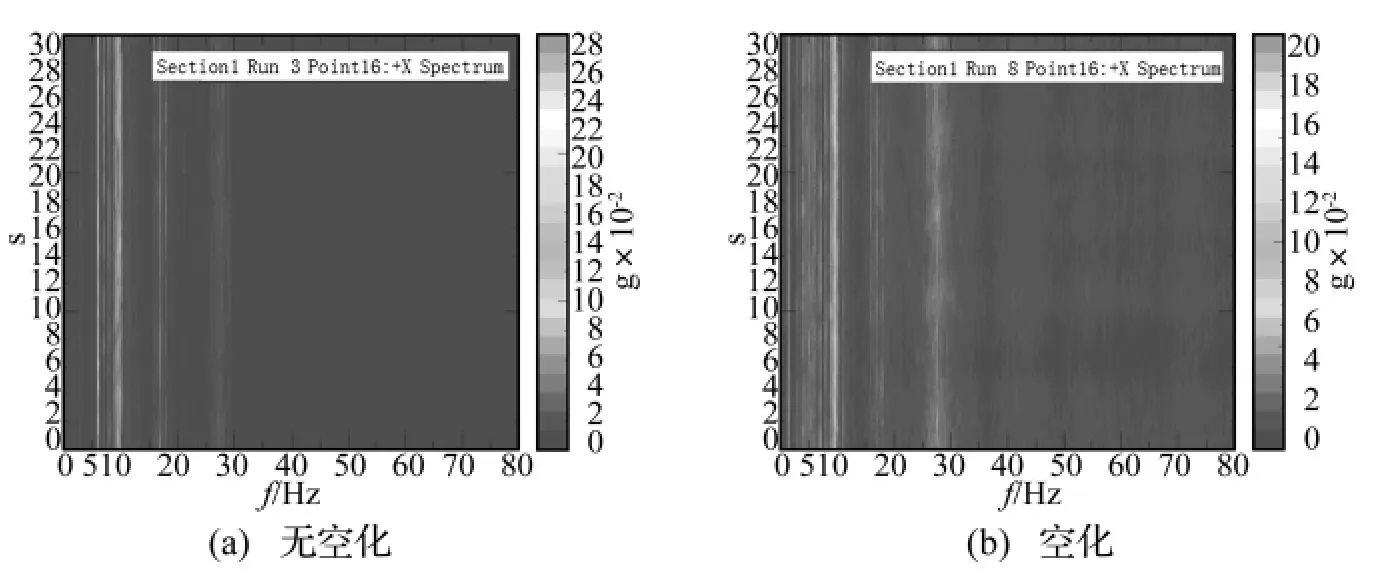
图2 蜗壳测点加速度响应云图Fig.2 Color map of spiral case acceleration

按前文所述方法，对各测点响应数据进行符号空间重构，组成结构整体符号空间矩阵，利用对应新符号的特征权系数矩阵分析。在符号空间内得到的两个工况下的特征值见表1。由于特征矩阵较大，这里不列出。

表1 符号空间特征值对比分析

Tab.1 Eigenvalue of symbolic space

序号 无空化 空化实部 虚部 幅值 实部 虚部 幅值1 92.23 0 92.23 －47.32 47.80 62.26 2 －290.3 464.9 548.1 －47.32 － 47.80 62.26 3 －290.3 － 464.9 548.1 720.1 1048 1272 4 －939.4 208.2 962.2 720.1 －1048 1272 5 －939.4 － 208.2 962.2 1362 436.3 1430 6 －691.5 1446 1603 1362 －436.3 1430 7 －691.5 －1446 1603 －1662 0 1662 8 1890 0 1890 －2235 0 2235 9 －2399 0 2399 －339.5 －2212 2238 10 1622 2077 2635 －339.5 +2212 2238

由表1可以看出，按符号空间方法分析该泵的性能，其特征值一般在2 000以下，并且空化时的数值明显加强。为验证符号空间方法的正确性，对该实验数据进行工作模态分析［9～11］。基于环境激励的工作模态分析方法仅需用测试的振动响应数据识别系统的模态参数，比传统的模态分析更能准确反映系统的实际动态特性，识别结果更符合实际情况和边界条件。取泵上各测点的响应数据，计算互功率谱(这里不考虑电机测点)如图3。由图3可以看出，各测点间互功率谱的主要峰值分布在2 000 Hz以下，与表1的结论基本吻合。利用LMS的Polymax分析方法［9］计算2个工况下泵的工作模态，其稳态图如图4。工作模态结果见表2。

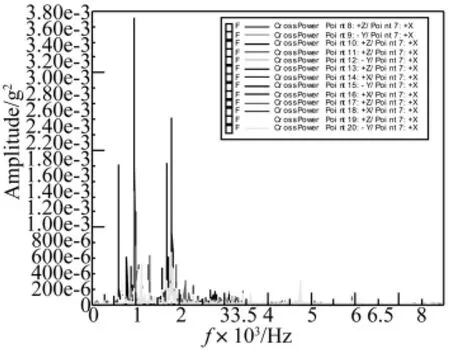
图3 空化工况各测点互功率谱Fig.3 Crosspower spectrum on cavitation condition

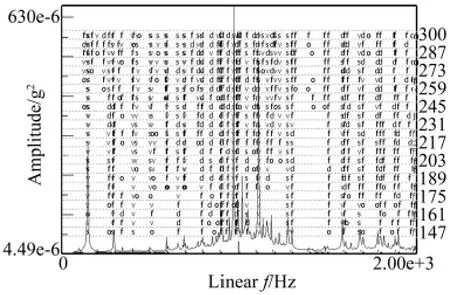
图4 空化工况频谱参数识别稳态图Fig.4 Stabilization diagram with cavitation

表2 离心泵工作模态分析结果Tab.2 Operational modal analysis of centrifugal pump

表1和表2的结果对比表明，离心泵工作模态和符号空间方法计算的结果比较接近。将符号空间识别方法的特征值与工作模态分析方法的模态频率对比，结果见图5，系列1为无空化工况下的工作模态频率，系列2为严重空化时的工作模态频率，系列3为无空化工况下的符号空间特征值，系列4为严重空化时的符号空间特征值。图5的结果表明，符号空间方法和工作模态方法计算得到的结果相近，且规律类似，但两种方法的结果仍有较大差别。工作模态方法的本质是研究泵的固有特性，只是不同环境激励下可能体现不同模态特征，但差别有限。符号空间方法是利用振动响应序列的Lempel-Ziv分析构建了符号空间，与物理空间和模态空间等是一种变换关系，该变换过程是一个非线性过程。这里应用与模态空间之间的类比关系，由图5可以看出符号空间方法计算结果明显比工作模态频率大，说明泵空化过程是一个复杂过程。基于符号空间的结构动力学状态估计方法是复杂结构整体特性评价的一个尝试，其特征值表现了结构的一定动力特性，但特征向量矩阵性质与动力学状态之间的关系问题，以及基于符号空间方法的状态估计参数及其参数灵敏度问题仍需进一步研究。

图5 符号空间方法与工作模态结果对比Fig.5 Comparison symbolic space method with operational modal analysis

3 结论

本文以某船用离心泵为例，测量了离心泵各工况下的振动和噪声响应，应用符号化方法和Lempel-Ziv复杂性分析建立了描述泵动力学性能的符号空间，对该泵的汽蚀状态进行识别。可以得到以下几点结论:

(1)实验测试、频谱分析、工作模态分析以及符号空间方法的结论都能看出该泵的振动主要特征频率和汽蚀作用特征频率都在2 000 Hz以下，反映了该泵的汽蚀特性。也验证了符号空间识别方法能较好地识别泵的汽蚀状态。

(2)基于振动响应序列符号化和Lempel-Ziv复杂性分析的结构动力学状态估计的符号空间方法可用于离心泵汽蚀状态的识别。符号空间方法的计算结果比工作模态频率大，说明了泵的空化过程是一个复杂过程。

(3)符号空间方法利用非线性变换，对结构动力学行为进行整体状态估计，对难以精确建模的结构复杂、环境复杂、信号复杂等问题提供一种有效分析方法，其在振动分析与控制领域内的应用将是一个可持续研究的方向，具有广阔的应用前景。

［1］黄国富，常 煜，张海民，等.低振动噪声船用离心泵的水力设计［J］.船舶力学，2009，4:313－318.

［2］ Ishizaki R，Shinba T，Mugishima G，et al.Time-series analysis of sleep wake stage of rat EEG using time-dependent pattern entropy［J］.Physica A，2008，387:3145 －3154.

［3］ Allison L，Stern L，Edgoose T，et al.Sequence complexity forbiologicalsequence analysis［J］. Computers and Chemistry，2000，24:43 －55.

［4］ Liu L，Wang T.Comparison of TOPS strings based on LZ complexity［J］，Journal of Theoretical Biology，2008.251:159－166.

［5］ Khatkhate A，Gupta S，Ray A，et al.Anomaly detection in flexible mechanical couplings via symbolic time series analysis［J］.Journal of Sound and Vibration，2008.311:608 －622.

［6］Li J K，Song X R，Yin K.The discrete capability of Lempel-Ziv complexity algorithm on vibration sequence［J］.Chinese physics letters，2010，27(6):060502.

［7］孙克辉，谈国强，盛利元.TD-ERCS离散混沌伪随机序列的复杂性分析［J］.物理学报，2008，57(6).

［8］ Lempel A，Ziv J.On the complexity of finite sequence［J］.IEEE Transaction on information theory，1976.1:75 －85.

［9］傅志方，华宏星.模态分析理论与应用［M］.上海交通大学出版社，2000.

［10］陈 林，张立民，段合朋.基于环境激励的车辆系统工作模态试验分析［J］.噪声与振动控制，2008，28(6):81 －84.

［11］ LMS company，LMS Test Lab manuals［M］.Leuven:LMS company，Belgium，2005.

［12］周 云，易伟建.用PolyMax方法进行弹性地基板的实验模态分析［J］.振动与冲击，2008，26(7):139－144.

Centrifugal pump cavitation state estimation based on complexity and symbolic space

SONG Xiang-rong1，LI Jian-kang2

(1.School of Naval Architecture and Ocean Engineering，Jiangsu University of Science and Technology，Zhenjiang 212003，China;2.School of Science，Jiangsu University，Zhenjiang 212013，China)

In order to construct a symbolic space to describ dynamic characteristics of a structure，vibration response sequences of several points were measured.Firstly，these sequences were converted to symbolic series by using the multi-segmented coarse-grained method.With Lempel-Ziv complexity analysis，a symbolic space was constructed.A centrifugal pump was studied as an example.Its cavitation state was estimated in the symbolic space.The results provided a novel method of state estimation to complex structures difficult to be modeled or ones working in complex environment.

Lempel-Ziv complexity;symbolic space;centrifugal pump;cavitation;state estimation

TH311

A

江苏省优势学科项目资助;江苏科技大学青年教师基金项目资助。

2010－06－02 修改稿收到日期:2010－07－19

宋向荣 男，硕士，副教授，1975年10月生