区间参数智能梁结构开环系统动力特性分析

王敏娟，陈建军，魏永祥，张 超，马洪波

(西安电子科技大学 机电工程学院，西安 710071)

区间参数智能梁结构开环系统动力特性分析

王敏娟，陈建军，魏永祥，张 超，马洪波

(西安电子科技大学 机电工程学院，西安 710071)

以区间参数压电智能梁结构为研究对象，在材料性能参数和几何尺寸为区间变量时采用区间分析法建立了结构质量矩阵和刚度矩阵的区间模型。从求解结构振动动态特性的Rayleigh商出发，利用区间变量运算法则推导出了结构开环系统固有频率的数字特征表达式。通过算例，考察了区间参数对结构固有频率特性的影响，验证了所建模型和方法的可行性与合理性。研究结果表明，文中利用区间系数分析法来研究压电智能梁结构开环系统的动力特性具有一定的工程应用价值。

动态特性分析;区间运算法则;区间系数;区间变量;压电智能梁

由于压电材料具有正、负压电效应且体积小、质量轻等一系列优点，使得其在智能结构的振动控制中具有广泛的应用前景。因此，研究智能结构系统振动特性的问题是一个非常有意义的课题。近年来，有关这方面的研究已有不少成果［1］问世，如:文献［2］建立了含压电传感器和执行器的智能结构平面梁单元模型，分析了在无外力而只有外电场作用下梁的静力位移响应;文献［3］分析了具有分布压电传感器和执行器的四边简支方板在开、闭环状态下的动态特性，讨论了模态形状和相应的模态电压以及各阶固有频率随反馈增益的变化情况;文献［4］采用随机因子法分析了随机参数智能结构的动力特性;文献［5］针对压电智能薄板结构，建立了具有12个位移自由度、2个电自由度的有限元模型，并分析了随机参数压电智能板结构的动态特性。然而，迄今为止所看到的智能梁结构动力分析几乎均属于确定性模型或概率模型，关于区间参数智能梁结构开环系统动力特性分析的文献鲜有报道。

在结构的分析与设计中，需要合理地定量处理对结构响应和性能起支配作用的各种参数所存在的不可避免的不确定性因素。概率理论在此领域曾发挥了重要的作用，得到了较为成功的应用，随机参数有限元方法成为不确定结构计算的最为普遍的方法。但概率模型的应用需要较多数据信息描述参数的概率分布类型，且通常计算量比较大。而概率数据的小误差可能导致结构的概率计算出现较大偏差。因此，概率模型在统计数据较少或计算模型不足够精确时，不是一种理想的模型。由于区间分析方法只需要给定参数取值的上下限范围即可，故近年来利用区间方法进行结构分析的研究日益受到重视，文献［6］提出了一种求解结构特征值问题上下界的区间计算方法，将该方法［7－8］加以拓广并应用于区间结构的闭环系统动力特性分析和区间参数结构的动力响应分析中。文献［9］提出了一种不确定性桁架结构区间有限元分析的区间因子法，文献［10］利用区间因子法分析了具有区间参数的智能桁架结构动力响应问题。文献［11－13］进一步将区间集合模型用于研究动力响应的灵敏度分析、可靠性问题以及误差分析，并获得了一些重要的结果。

本文以压电智能梁结构为研究对象，利用区间分析法建立了结构的质量矩阵和刚度矩阵的区间模型。并通过算例分析了结构物理参数和几何尺寸分别或同时为区间变量时对结构开环系统动力特性的影响。其结果表明，在掌握的原始数据较少的情况下，区间分析法处理压电智能梁结构开环系统的动力特性问题是一种比较方便、可行而有效的方法。

1 智能梁结构的动力学有限元方程

考虑一长为L、宽为w、厚为H且各向同性的平面弹性梁，其上下表面均匀地粘贴一层厚度均为h压电片，上表面的传感层和下表面的致动层均采用相同的材料。整个梁沿轴线方向被离散为ne个单元，相邻两个单元上的压电片电极之间彼此绝缘，并假设一个压电片只有两个电自由度。令其单元外加作用载荷Fep=0，单元阻尼矩阵Ce=0，则由Hamilton原理并按有限元方法进行扩阶和叠加后，可得压电智能梁结构的整体动力学有限元微分方程［2］为:

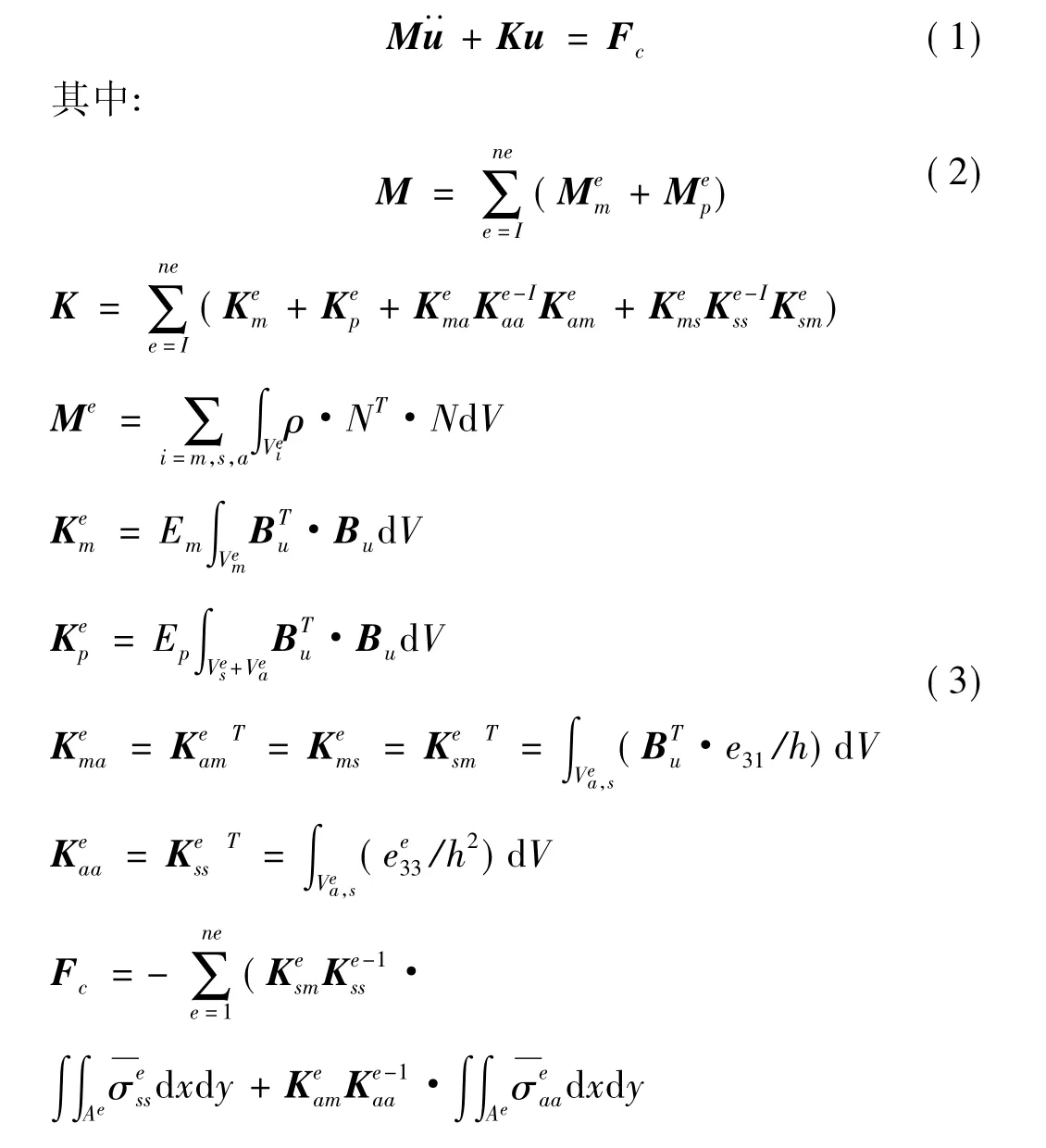
令Fc=0，可得结构开环系统的有限元方程为:

2 区间参数压电智能梁结构的不确定性分析

2.1 区间分析法

设R为实数域，对于给定的两个实数Xl，Xu∈R，且 Xl≤Xu，则有:

其中，Xl为有界闭区间;Xl、Xu为区间变量X的上下界;Xc=(Xl+Xu)/2为区间变量Xl的均值或中间点;Xr=(Xu－Xl)/2为区间变量Xl的离差或半径;令δ=Xr/Xe=(Xu－Xl)/(Xl+Xu)为区间Xl的区间变化率。令 η =Xl/Xc，则 Xl= ηXc，η∈［Xl/Xc，Xu/Xc］，可知 η的区间均值为1。由此可见，区间系数η描述了区间变量Xl的不确定性，对任意已知上下界的区间参数而言，均可求出其相应的区间系数。

2.2 质量矩阵与刚度矩阵区间模型的建立

结构参数由于各种客观原因存在不确定性因素，必将导致智能梁结构刚度矩阵和质量矩阵的不确定性，并最终导致结构特征值问题的不确定性。但结构参数不确定性的幅度或界限较易确定，如何建立区间参数结构的刚度矩阵和质量矩阵，是区间参数结构动力特性分析必须首先解决的问题。

根据区间运算法则［14］，可得出如下关系式的变换:

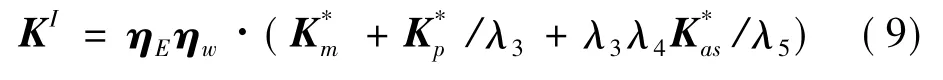
3 区间参数智能梁结构动力特性的数字特征

对结构动力特性的分析涉及到各阶固有频率和所对应的固有振型向量，两者为一一对应关系，且完全正相关。因此，确定了结构的每一阶固有频率也就确定了与之相对应的固有振型。故只需分析结构的固有频率。将式(6)和式(9)代入结构动力学Rayleigh商表达式，结合文献［15］中的区间特征值表达式，即:

4 算例

压电智能悬臂梁结构单元划分与节点编号见图1所示，其传感层和致动层都是由同一种PVDF压电材料均匀地粘贴在弹性体的上、下表面。沿梁的轴向被均匀地离散为4个单元，其中节点编号由左向右依次为1、2、3、4、5，单元编号由左向右依次为:①、②、③、④。每个单元的长度l为(7.35，8.65)cm，其上下两层压电片厚度 h 同为(0.075，0.125)mm，基梁厚度 H=(4.37，5.63)mm，梁宽 w=(4.83，5.17)mm，且几何尺寸的区间分散性相同。PVDF的物理区间参数取值分别为:压电常数为 e31=(0.045，0.047)C/m2，压电体的介电常数为，压电体的弹性模量为 Ep=(1.97，2.03) ×109N/m2，质量密度为 ρp=(1.695，1.905) ×103kg/m3。弹性体的物理区间参数为:质量密度 ρm=(7.695，8.305) ×103kg/m3，弹性模量 Em=(1.83，2.37) ×1011N/m2。

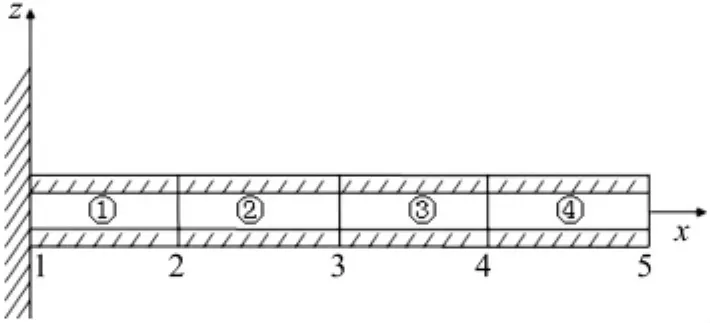
图1 智能悬臂梁结构图Fig.1 Intelligent cantilever beam

依据公式(12)、(13)和式(15)，在结构物理参数和几何尺寸分别或同时为区间变量时，可通过区间运算计算得出结构固有频率ωi的区间系数的区间均值以及的上下界取值范围，如表1所示。对应于表1中所得到的区间系数，在表2中相应地给出了压电智能悬臂梁结构开环系统的三种区间模型。其中区间模型Ⅰ为结构物理参数为区间变量时前5阶固有频率的计算结果，区间模型Ⅱ为结构几何尺寸取区间变量时前5阶固有频率计算结果，区间模型Ⅲ为结构物理参数和几何尺寸同时为区间变量时前5阶固有频率计算结果。同时，分别列出了在物理参数与几何参数分别和同时为区间变量时结构固有频率的区间变化率。为了对比本文方法的正确性与合理性，文中给出了所有区间变量取区间均值时以及区间参数同时取上限和下限时结构开环系统固有频率的确定性模型计算结果。

对比表2中区间变化率的计算结果可知，在结构几何参数和物理参数的区间分散性相同的情况下，前者对结构系统固有频率的区间分散性影响较大;在结构物理参数和几何参数同时为区间变量时，结构固有频率的区间变化率将显著增大。因此，在不确定性结构的分析中，结构参数的区间分散性是不容忽视的。

表1 固有频率区间系数的取值范围Tab.1 Value range of interval coefficient of natural frequency

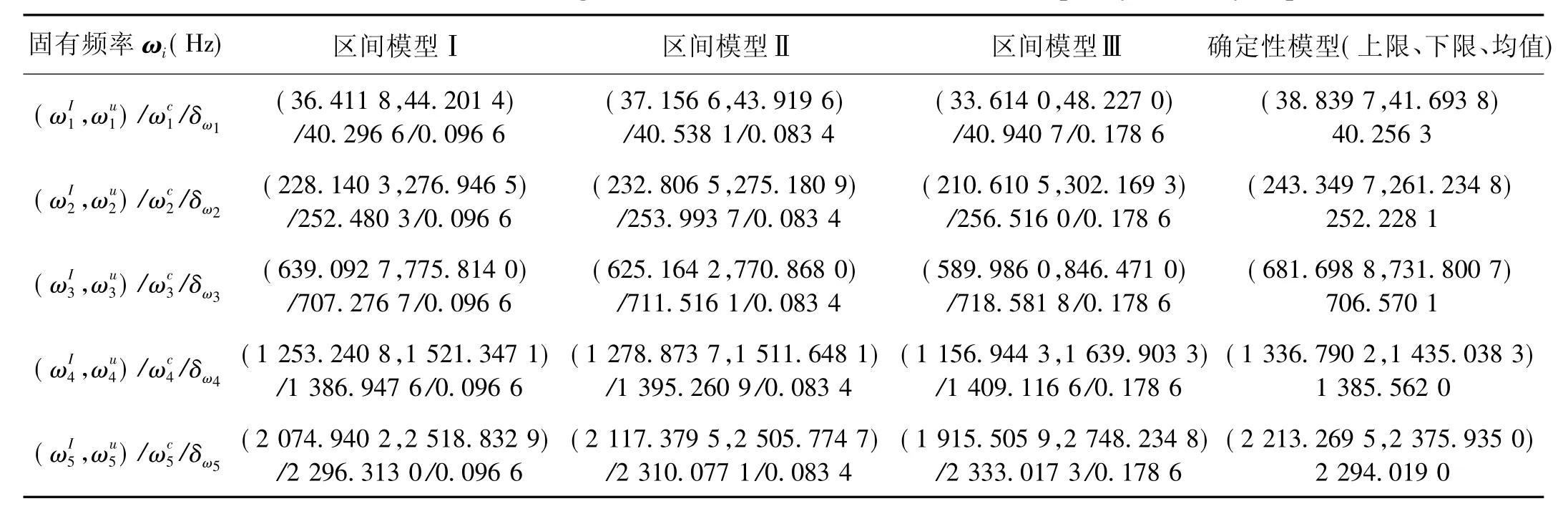
表2 各阶固有频率取值范围及区间均值的计算结果Tab.2 Results of value range and interval mean value of natural frequency for every step

5 结论

文中基于区间分析法构建了压电智能梁结构的质量和刚度矩阵的区间模型，并在结构的物理参数和几何参数均为区间变量的情况下，利用区间系数法分析了区间参数压电智能梁结构固有频率的数字特征。

通过算例考察了文中所建立的区间参数压电智能梁结构的有限元模型是合理的。该方法的优点在于只需已知系统中诸区间参数的上下界，即可反映出任一区间参数对压电智能梁结构固有频率区间分散性的影响程度。对比算例中确定性模型的计算结果可知:文中的求解方法是可行且有效的。

［1］Hwang W S，Park H C.Finite elementmodeling of piezoelectric sensors and actuactors［J］.AIAA，1993，31(5):930－937.

［2］陈塑寰，马爱军，刘中生.智能结构的梁有限元模型［J］，宇航学报，1997，18(2):72－77.

［3］曹宗杰，闻邦椿，陈塑寰.含压电材料智能结构动态特性的研究［J］.计算力学学报，2001，18(3):267－27.

［4］Chen J J，Che J W，Sun H A，et al.Probabilistic synamic analysis of truss structures［J］.Structural Engineering ＆Mechanics，2002，13(2):231 －239.

［5］陈建军，王小兵.随机参数智能板结构的动态特性分析［J］.西安电子科技大学学报，2004，31(5):661 －665.

［6］ Qiu Z P，Chen S H，Elishakoff I.Natural frequencies of structures uncertain but nonrandom parameters［J］.Journal Optimization Theory and Applications， 1995， 86(3):669－683.

［7］Chen S H，Zhang X M，Chen Y D.Interval eigenvalues of closed-loop systems of uncertain structures［J］.Computers ＆Structures，2006，84(3－4):243－253.

［8］CHEN S H，Wu J.Interval optimization of dynamic response for structures with interval parameters［J］.Computers ＆Structures，2004，82(1):1 －11.

［9］马 娟，陈建军，张建国.不确定性桁架结构区间有限元分析的区间因子法［J］.机械设计与研究，2005，21(6):6－9.

［10］林立广，陈建军，马 娟，等.基于区间因子法的不确定性桁架结构动力响应分析［J］.应用力学学报，2008，25(4):612－617.

［11］ Moens D，Vandepitte D.Interval sensitivity theory and its application to frequency response envelope analysis of uncertain structures［J］.Computer Methods in Applied Mechanics and Engineering，2007，196(21 － 24):2486－2496.

［12］ Adduri P R，Penmetsa R C.Bounds on structural system reliability in the presence of interval variables［J］.Computers and Structures，2007，85(5－6):320－329.

［13］Zalewski B F，Mullen R L，Muhanna R L.Interval boundary element method in the presence ofuncertain boundary conditions，integration errors，and truncation errors［J］.Engineering Analysis with Boundary Elements， 2009，33(4):508－513.

［14］邱志平著.非概率集合理论凸方法及其应用［M］.北京:国防工业出版社，2005.

［15］Chen S H，Qiu Z P，Song D T.A new method for computing the upper and lower bounds on frequencies of structures with interval parameters［J］.Mechanics Research communication，1994，21(6):583－592.

Dynamic characteristic analysis of an open-loop system for an intelligent beam with interval parameters

WANG Min-juan，CHEN Jian-jun，WEI Yong-xiang，ZHANG Chao，MA Hong-bo

(School of Electromechanical Engineering，Xidian University，Xi'an 710071，China)

Structures with a piezoelectric intelligent beam were taken as study objects here.According to the method of interval analysis，the interval models of mass matrix and stiffness matrices with interval variables for structural physical parameters and geometric dimensions were built.From Rayleigh quotient for dynamic characteristic of structural vibration，and based on the interval algorithms，the computation expressions of natural frequencies of a structural openloop system were deduced.Through an example，the effects of the uncertainty of the structural interval parameters on the structural natural frequency were inspected，and the model constructed and the method proposed here were verified.It was shown that the interval coefficient method is applicable in dealing with the dynamic characteristic of an open-loop system of an intelligent beam.

dynamic characteristic analysis; intervalalgorithms; intervalcoefficient; intervalvariables;piezoelectric intelligent beam

O324

A

国家863高技术研究发展计划项目(2006AA04Z402);国家自然科学基金项目(50905134)资助

2010－08－31 修改稿收到日期:2010－11－18

王敏娟 女，博士生，1981年生