基于模态应变能和小波变换的结构损伤识别研究

严 平，李胡生，葛继平，叶黔元

(1.上海理工大学 环境与建筑学院，上海 200093;2.上海应用技术学院 城市建设与安全工程学院，上海 200235)

基于模态应变能和小波变换的结构损伤识别研究

严 平1，2，李胡生2，葛继平2，叶黔元1

(1.上海理工大学 环境与建筑学院，上海 200093;2.上海应用技术学院 城市建设与安全工程学院，上海 200235)

针对单一方法对结构同时发生多处不同程度损伤识别的不敏感性缺陷，结合小波变换在时域、频域内表征信号局部特性且能够聚焦到信号或函数的任意细节进行处理的能力，提出了一种基于单元模态应变能和小波变换的结构损伤识别方法。在单元模态应变能基础上，利用小波变换系数的变化和分布情况构建单元模态应变能小波变换结构损伤指标，通过对简支梁的数值模拟和斜拉桥模型试验研究的结果与单元模态应变能平均变化率作为损伤识别指标的计算结果进行对比，结果表明该方法能有效确定结构同时发生多处不同程度损伤的位置和估计损伤程度，为实际工程应用奠定了基础。

结构损伤识别;独塔斜拉桥;模态应变能;小波变换;试验研究

近年来，随着现代工业技术与结构振动分析理论的迅速发展，结构健康监测技术已经发展成为一门建立在损伤机理、传感器技术、信号分析技术、计算机技术及人工智能技术之上的多学科综合性技术。其中，核心问题是结构损伤识别方法的研究，基于结构动力特性和动力响应的损伤识别方法是近年来研究的热点。目前，学者提出了许多基于模态的损伤识别指标，主要有频率、振型、曲率模态等。这些指标对损伤的敏感程度差别较大，He［1］综述了模态应变能指标的发展历程，基于模态应变能的损伤识别综合考虑了振型、频率、单元刚度等因素的影响，对损伤具有较强的敏感性。

虽然在模态应变能变异指标进行损伤识别方面进行了大量的研究工作，取得了丰硕的研究成果，但对结构同时发生多处不同程度损伤的研究较少。在各种损伤识别方法中，对同时发生多处不同程度损伤较大处能很好地进行识别，对损伤程度相对较小处往往被忽略。而小波变换具有表征信号时域和频域局部特性的能力，能够聚焦到信号或函数的任意细节进行时、频域处理，适合分析和识别结构响应中其它方法难以发现的局部损伤信息，检测结构的损伤情况［2］。

因此，本文作者利用模态应变能和小波变换的优点，将结构模态应变能和小波变换有机结合起来，利用模态应变能小波变换系数的残差作为损伤识别指标，对结构进行损伤识别。首先，用数值仿真对混凝土简支梁进行损伤识别，并与单元模态应变能平均变化率作为损伤识别指标的计算结果进行对比，验证该方法的有效性。然后采用该方法对一室内斜拉桥模型进行损伤识别研究，验证该方法的实用性。结果显示，基于单元模态应变能小波变换损伤识别法能有效确定结构同时发生多处不同程度(差值不大于20%)损伤的位置和估计损伤程度。

1 模态应变能理论

在众多损伤标识量中，模态应变能能够反映结构局部特性的变化，并可以通过各阶振型和刚度矩阵得到，且对局部结构的敏感性大大高于振型，因此模态应变能以其对结构局部损伤的敏感性和较好的抗噪性能受到广泛关注。然而，结构损伤一般是结构局部刚度的损失，而与质量无关。针对这一特点，本文以单元模态应变能作为结构损伤的判断基本因子。

对于梁式结构而言，结构损伤前第j个单元关于第i阶模态的单元模态应变能(MSE):

同理，结构损伤后第j个单元关于第i阶模态的单元模态应变能(MSEd):

式中:aj和aj+1分别为节点j和j+1的x坐标，(EI)j为第j个单元的抗弯刚度，上标“d”表示结构损伤，{Φi}为结构第i阶模态振型。

对于实验模态分析而言，结构受损后的抗弯刚度(EI)d是无从得知的。因此，用受损前的抗弯刚度EI代替受损后的抗弯刚度(EI)d，并考虑当选取的梁单元相对较小时，第j个单元的抗弯刚度(EI)j可以近似为常量，则式(1)和式(2)可写成:

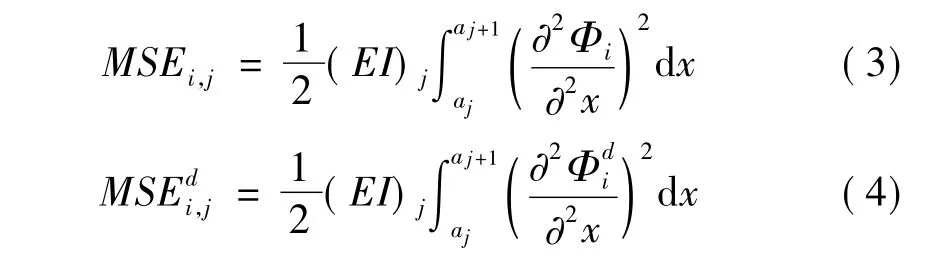
结构损伤前后的单元模态应变能变化(MSEC)为(略去高阶项):

文献［3，4］证明了单元模态应变能变化是对结构损伤敏感的定位指示因子，可用来诊断结构的损伤位置。定义模态应变能变化率(MSECR)作为识别损伤的指标:

为降低试验模态振型随机噪声的影响，可同时用多阶模态振型来诊断结构的损伤位置，考虑它们的平均值得到第j个单元用m阶模态振型计算的单元模态应变能变化率(MSECRj):

2 小波变换理论

在单一损伤识别方法中，对于同时发生多处不同程度损伤的较大处能很好地识别，对相对较小处则往往被忽略。而小波变换具有表征信号时域和频域局部特性的能力，能够聚焦到信号或函数的任意细节进行时、频域处理，适合分析和识别结构响应中其它方法难以发现的局部损伤信息，检测结构的损伤情况。

2.1 小波变换

小波变换是一种窗口大小固定，但其形状可改变的时频局部化分析方法。小波变换对信号具有良好的自适应性，可以对非稳态信号进行多分辨率分析，为信号检测、特征参数提取、故障诊断与定位等方面提供了一条有效的途径。

小波变换的思想来源于伸缩与平移方法，每个小波函数都有两个参数:尺度因子 a和平移因子b，a、b均为实数。设ψ(x)∈L2(R)(L2(R)表示平方可积的实数空间，即能量有限的信号空间)，若函数ψ(x)被认定为是一个母小波函数，则分别用a、b伸缩和平移后，产生一系列小波函数:

对于任意函数或信号f(x)∈L2(R)的小波变换为:

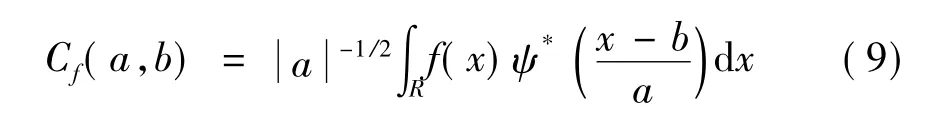
式(7)是一个关于a和b的二元函数(上标 *代表取共轭)，体现以ψa，b(x)为标准f(x)的变化快慢情况，当取小尺度时，小波沿x轴收缩，小波变换将给出被分析信号的局部信息;当取大尺度时，小波沿x轴膨胀，小波变换将给出被分析信号的整体信息。

结构损伤一般是结构局部刚度的损失，结构一旦发生损伤，损伤部位的单元模态应变能将出现难以直接观测到的微小突变。利用小波变换对局部信号进行放大，可通过小波变换系数的变化更好地分析和确定信号中的突变点，有效地确定损伤的存在和损伤位置。

2.2 小波函数选取

小波分析在工程应用中，一个十分重要的问题是最优小波基的选择问题，这是因为不同的小波基分析同一问题会产生不同的结果。根据小波函数选取的通常标准:

(2)对称性;

(3)ψ和φ(如果存在)的消失矩阶数;

(4)正则性。

结合本文研究的信号特征和分析目的，在小波变换过程中本文采用能实施快速变换、正交的、正则性和消失矩较好的bior6.8小波函数来检测局部突变信号，此时结构损伤信号的局部突变将引起小波变换系数比较明显的变化［2，5］。

2.3 模态应变能和小波变换损伤识别

具体考虑梁结构的振动方程:

式中:［M］、［C］、［K］分别为质量、阻尼和刚度矩阵，y为梁弯曲变形挠度。

引入模态坐标q(t)，则弯曲变形挠度y可表示为:

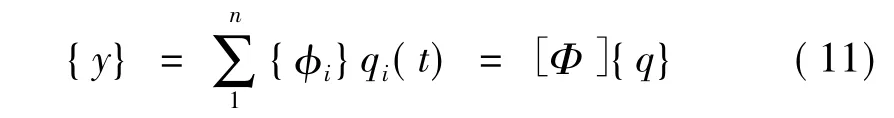
式中:φi和Φ分别代表位移模态振型和模态矩阵。将式(11)代人方程(10)并求解方程得到r阶模态响应:

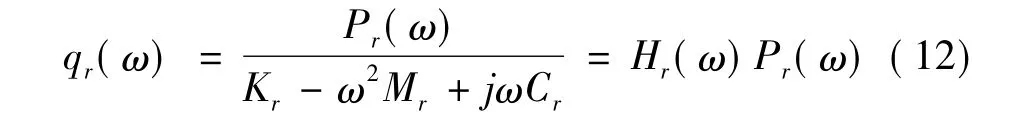
式中:Mr、Cr、Kr分别为模态质量、阻尼和刚度，Hr(ω)为频响函数，Pr(ω)为r阶广义力。根据位移模态振型由式(3)和式(4)可求出结构损伤前后第 j个单元关于第i阶模态的单元模态应变能MSEi，j。

在进行信号分析时本文采用三次样条插值法拟合式(3)和式(4)，进而进行小波变换。通过此方法对信号特征处理非常敏感，小波变换系数的变化情况极易识别结构损伤。用MSEDCi，j表示结构损伤前后第i阶模态应变能下第j个单元的小波变换系数差，按下式计算:

为降低试验模态振型随机噪声的影响，可同时用多阶模态振型来诊断结构的损伤位置，考虑它们的平均值得到第j个单元用m阶模态振型计算的单元模态应变能小波变换系数变化情况的损伤指标MSEDj:

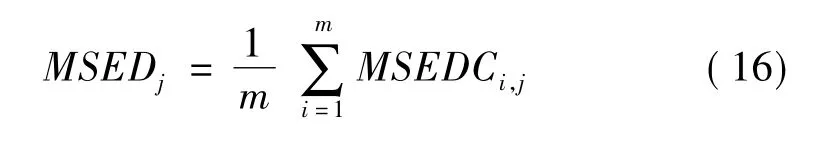
3 数值算例

本文以一简支混凝土梁为例，如图1所示。其几何尺寸和材料特性参数为:梁长l=6.0 m，矩形梁截面尺寸 b×h=0.3 m ×0.5 m，截面惯性矩 I=0.001 125 m4，材料的弹性模量 E=3.0 ×1010N/m2，泊松比 ν=0.2，密度ρ=2.6×103kg/m3。将梁等长划分为24个单元，每个单元长度为0.25 m，共25个节点。

图1 简支梁有限元模型Fig.1 Finite model of simple beam

结构损伤一般是结构局部刚度的损失，数值模拟中用单元刚度降低来模拟混凝土梁损伤，分8种损伤工况如表1所示。

表1 单元损伤工况Tab.1 Damage condition of element

由于测试系统和测试环境的影响，在观测信号中不可避免地存在噪声。为了考虑噪声对结构损伤识别的影响，本文在模拟数据中加入均值为零的白噪声得到含噪声信号:

式中:σ为均值为零的白噪声。考虑到模拟损伤程度的大小和实际工程中噪声的大小，本文拟采用2%的噪声进行模拟。图2为工况5损伤前后前四阶模态，显然单从模态曲线是很难确定损伤发生和损伤位置。

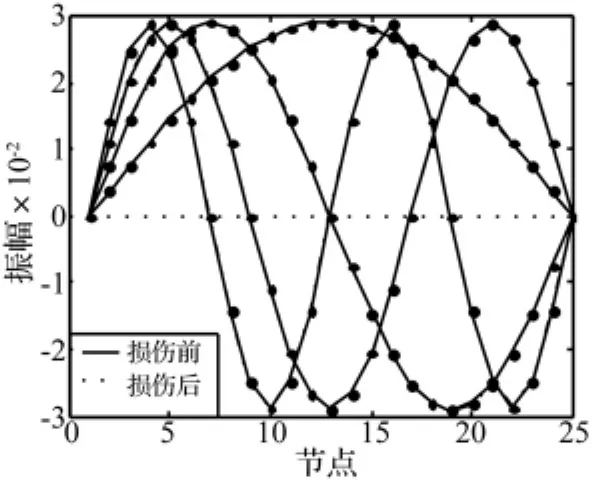
图2 工况5损伤前后前四阶模态Fig.2 First four mode damage of condition 5

3.1 单处损伤

考虑前四阶模态，分别以式(7)定义的MSECRj和式(16)定义的MSEDj作为损伤标识量并计算其值，单处损伤的前三种工况识别结果如图3所示。

图3 单处损伤指标MSECR、MSED识别结果Fig.3 The simply damage identification result of MSECR or MSED

从图3中可知，当结构发生一处损伤时，损伤指标MSECRj和MSEDj在不同的损伤程度下单元9处会发生突变，由此可推出该处可能出现损伤，且MSEDj指标法比MSECRj指标法损伤识别的抗噪性好，不容易产生误判。随着损伤程度的增加，损伤指标MSEDj比MSECRj的值变化更明显。因此，采用单元模态应变能小波变换损伤识别方法能更好的识别单处不同程度损伤，具有良好的抗噪性。

3.2 两处损伤

考虑前四阶模态，分别以式(7)定义的MSECRj和式(16)定义的MSEDj作为损伤标识量并计算其值，两处损伤的后五种工况识别结果如图4所示。

由图4(a)可知，对两处损伤程度相同情况下本文所述两种方法均能较好地识别出损伤。从图4(b－e)可知，对两处不同程度的损伤，MSECRj指标法只能识别出损伤程度较大处，较小处则容易被忽略。而MSEDj指标法则能有效地识别出两处损伤程度差值在20%以内的损伤，且具有良好的抗噪性，不易产生误判。

因此，无论是单处损伤还是多处不同程度的损伤，MSEDj指标法均能通过MSEDj的改变而产生的突变有效地识别损伤位置，具有良好的抗噪性。如图5所示，对不同程度的损伤，MSEDj变化明显且随着损伤程度的变大而增大，能更好地了解损伤的程度。

图4 两处损伤指标MSECR、MSED识别结果Fig.4 The two place damage identification result of MSECR or MSED

图5 单元9损伤程度变化Fig.5 Change of element 9 damage extent

4 模型试验分析

4.1 试验模型

本斜拉桥模型采用单塔斜拉桥形式，两跨对称布置，模型全长5.2 m;塔梁铰结，索塔形式采用门式，塔高1.83 m，设三道横梁，横梁上锚固斜拉索;斜拉索采用稀索扇式布置，单面设六根索，全桥共设十二根索，斜拉索采用3 mm的钢丝。纵向主梁采用30 mm×30 mm×2.5 mm的角钢，桥面板为1 mm厚的薄钢板，桥宽0.47 m。墩高0.58 m，索塔和桥墩材料均为60 mm×100 mm×2 mm的槽钢。斜拉桥的总体布置图和实物图如图6和图7所示。

图6 斜拉桥模型三视图Fig.6 Different view of cable-stayed bridge model

本文采用对一侧主梁角钢进行切口的方式来模拟损伤。试验研究采用密布传感器的锤击试验方法将斜拉桥模型分6个测段进行测量［6］，测点1－33沿纵桥向等距布置，其中测点R为参考点，位于左侧跨的3/16处;损伤位置一位于测点12和测点13中间;损伤位置二位于测点25和测点26中间，如图8所示。试验研究中分两种损伤工况:① 只有位置二损伤;② 位置一和位置二同时损伤。位置一损伤切口深度为1 cm，经计算主梁损伤位置一截面处刚度减小63%，对应斜拉桥模型在该损伤位置的整体截面刚度减少20%左右;位置二损伤切口深度为2 cm，经计算主梁损伤位置二截面处刚度减少75%，对应斜拉桥模型在该损伤位置的整体截面刚度减少30%左右。试验采用INV9824 ICP加速度传感器、INV3018C型智能信号采集处理分析仪。采样频率为100 Hz，频率分析通过峰值法确定，模态振型通过自谱互谱之间的相互关系确定［6－8］。

图7 斜拉桥模型实物图Fig.7 Photo of cable-stayed bridge model

图8 测点布置图Fig.8 Arrangement of sensor plan

4.2 试验结果分析

通过试验可测得斜拉桥模型的各阶模态振型，在进行信号分析时本文采用三次样条插值法进行拟合，图9为该桥试验模型频率分别为 9.125、12.000、35.625、43.375(Hz)对应的四阶无损试验模态。从该图中可知，实际试验中由于受到噪音、传感器的疏密布置、采集仪器本身的灵敏度等方面的影响，试验模态并没有如数值仿真中得到的模态理想，但试验模态数据亦能对结构的损伤进行有效识别。

图9 前四阶试验模态Fig.9 First four experimental mode

考虑测得的四阶试验模态，分别以式(7)定义的MSECRj和式(16)定义的MSEDj作为损伤标识量并计算其值。单处损伤识别结果如图10所示，对结构的单处损伤，本文所述两种方法均能很好地识别损伤的位置，具有良好的抗噪性。两处损伤识别结果如图11(a)可知，MSEDj指标法对试验模型两处损伤的位置二可以有效识别，对损伤程度较小处则无法识别，易产生误判、抗噪性差。从(b)图中可知，MSEDj指标法能有效地对试验模型的两处损伤进行识别，通过MSEDj幅值的大小可估计不同位置损伤程度的相对大小，且具有良好的抗噪性。

图10 单处损伤指标MSECR、MSED识别结果Fig.10 The simply damage identification result of MSECR or MSED

图11 两处损伤指标MSECR、MSED识别结果Fig.11 The two place damage identification result of MSECR or MSED

综上所述，通过斜拉桥模型的试验研究验证了MSEDj指标法能够有效确定结构同时发生多处不同程度损伤的位置和估计损伤程度，具有良好的抗噪性。

5 结论

本文作者利用小波变换在时域、频域内表征信号局部特性且能够聚焦到信号或函数的任意细节进行处理的能力，提出了一种基于模态应变能的小波变换结构损伤识别方法。通过数值模拟和斜拉桥模型试验分析研究，结果表明:

(1)通过分析比较MSECRj指标法和MSEDj指标法的识别结果，损伤指标MSEDj能较好地从结构响应信号中提取损伤信息，根据损伤尖峰沿结构的分布情况能有效地识别损伤的位置。

(2)通过比对两种方法的识别结果还可以看出，MSEDj指标法具有良好的抗噪性能。

(3)文中分析可知，指标MSEDj比MSECRj对损伤更为敏感，损伤程度越大，损伤尖峰的幅值也越大，但需要进一步研究探讨用损伤尖峰幅值估计结构损伤程度。

［1］He X.Vibration-based damage identification and health monitoring of civil structures［D］.University of California，San-Diego，2008.

［2］孙增寿，韩建刚，任伟新.基于曲率模态和小波变换的简支梁桥损伤识别方法［J］.郑州大学学报(工学版)，2005，26(3):24－27.

［3］史治宇，罗绍湘，张令弥.结构破损定位的单元模态应变能变化率法［J］.振动工程学报，1998，11(3):356 －360.

［4］Shi Z Y ，Law S S，Zhang L M.Structural damage detection from modal strain energy change［J］.Journal of engineering mechanics，2000:1216 －1223.

［5］杨晓楠，姜绍飞，唐和生，等.小波函数的选择对结构损伤识别的影响［J］.沈阳建筑大学学报，2005，21(6):635－639.

［6］葛继平，李胡生，陈 明.基于模态应变能变异指标的斜拉桥模型损伤识别研究［J］.武汉理工大学学报(交通科学与工程版)，2011，35(2):55 －59.

［7］李德葆，陆秋海.实验模态分析及其应用［M］.北京:科学出版社，2001.

［8］闵志华，孙利民，淡丹辉.影响斜拉桥模态参数变化的环境因素分析［J］.振动与冲击，2009，28(10):99 －105.

［9］Hsu T Y，Loh C H.Damage diagnosis of frame structures using modified modal strain energy change method［J］.Journal of engineering mechanics，2008:1000 －1012.

［10］葛继平，李胡生.基于小波包能量累积变异的梁桥损伤识别试验研究［J］.振动、测试与诊断，2011，31(1):85－88.

Structural damage identification based on modal strain energy and wavelet transformation

YAN Ping1，2，LI Hu-sheng2，GE Ji-ping2，YE Qian-yuan1

(1.School of Environment and Architecture，University of Shanghai for Science and Technology，Shanghai 200093，China;2.School of Urban Construction and Safety Engineering，Shanghai Institute of Technology，Shanghai 200235，China)

Single identification method is not sensitive to structural multiple different level damages.An approach of structural damage identification based on modal strain energy and wavelet transformation with the ability to denote local features of a signal in time domain or frequency domain and to process any details of a signal or a function was proposed.The structural damage index was built with the change and distribution of wavelet transformation coefficients based on elemental modal strain energy.Through numerical simulation of a simply supported beam and a cable-stayed bridge model experiment study，compared with the elemental modal strain energy method，the proposed method could effectively determine multiple different level damage locations in a structure and estimate damage levels.The results laid a foundation for the practical engineering applications of the proposed method.

structural damage identification;cable-stayed bridge;modal strain energy;wavelet transformation;experimental study

TU 317

A

上海市科学委员会重点科技攻关项目(072105115);铁道部科研项目(2010G007－J);上海市教委优青项目资助(YYY09007)

2011－02－17 修改稿收到日期:2011－05－04

严 平 男，硕士，1985年5月生

李胡生 男，博士后，1960年3月生