正确理解变压器原线圈上的电流

陈丹燕

(绍兴市第一中学 浙江 绍兴 312000)

如图1所示，变压器原线圈和交流电源相连，副线圈不接负载时，称变压器空载.变压器空载时，“副线圈上电流I2为零”的正确性毫无疑问.但有的教师和学生对于“此时原线圈上的电流I1是否等于零”这一点却颇感疑惑.

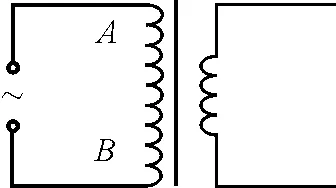
图1

上述两种说法似乎各有道理，但结论却完全相反.那么此时变压器原线圈上到底有没有电流呢？要回答这个问题，我们必须正确理解变压器的变流比公式.下面，将从变压器的能量转化和工作原理进行分析说明.

1 从能量转化的角度分析

设理想变压器副线圈开路，原线圈接入如图2所示交变电压

uAB=Umcosωt

(1)

原线圈中会产生阻碍电流变化的自感电动势

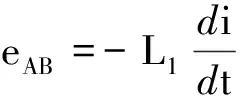
又因为理想变压器

uAB=-eAB

故

即

两边积分后得

(2)

式(2)表明：此时原线圈中电流不为零，如图3中虚线所示，除非L1→∞,才会有i→0.

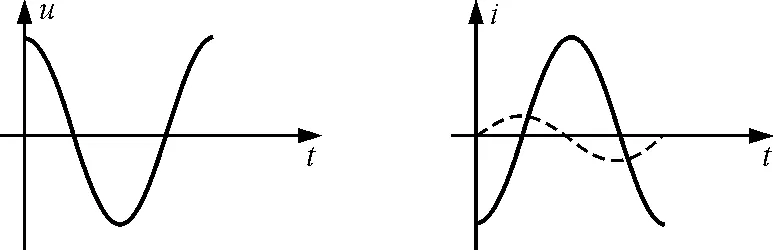
图2 图3

从图3中，也可以看出，i有时与uAB方向相反，需要克服电源电压做功；i有时与uAB方向相同，电源对其做功，似乎在循环往复.下面计算一个周期内的总功.

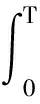
把式(1)、(2)代入后得

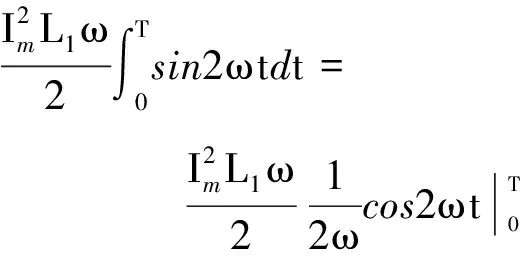
(3)

(4)

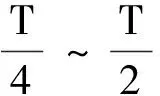
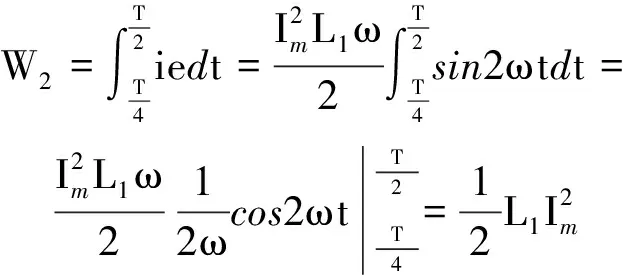
(5)

由此可见，理想变压器开路时，原线圈中有电流，其所起的作用是给电能和磁能之间的互相转化提供了桥梁.有时电能转化成磁能，有时磁能转化成电能.但一个周期内总功为零，不对外输出能量，我们称此为“有功功率等于零”，这样的电流，称为无功电流，用i0表示.

2 从电磁感应的角度分析

2．1需用到的基本物理量

如图4所示，设原线圈接入交流电压uAB，分别在原、副线圈上产生电流i1和i2，变压器铁芯中产生磁通量Φ.这些量都随时间做周期性变化，暂设Φ=Φ0sinωt.

此时，原、副线圈的磁通匝链数分别为

Ψ1=N1Φ

(6)

Ψ2=N2Φ

(7)

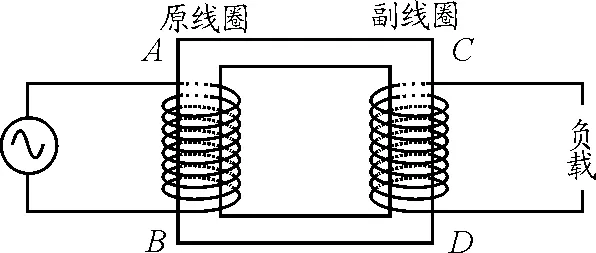
图4

又因为线圈中磁通量的产生，既有i1的贡献(自感磁通)，又有i2的贡献(互感磁通)，故磁通匝链数又可表示为

Ψ1=N1Φ=L1i1+M21i2

(8)

其中，M21表示副线圈对原线圈的互感系数.同理，对于副线圈也成立

Ψ2=N2Φ=L2i2+M12i1

(9)

其中，M12表示原线圈对副线圈的互感系数.可以证明M21和M21相等(此处略)，一般用M表示.

2．2规律推导说明变流比公式

考虑到理想变压器，原副线圈上没有电阻，可得交流电源对原线圈的输出电压与原线圈上自感电动势的关系为

uAB=-eAB

又因为

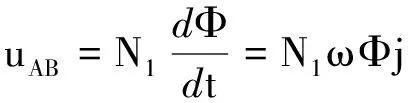
(10)

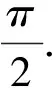
(1)空载时

i2=0 ，式(8)可简化为

N1Φ=L1i0

(11)

即

此原线圈上的电流只是让线圈中产生磁通Φ，故称励磁电流，也即本文第一部分中提到的无功电流.因理想变压器的L1→∞，故励磁电流(无功电流)i0→0.

(2)接负载时

当副线圈接有负载时，i2不等于零,会产生附加磁通.但因为原线圈的输入电压uAB没有变，线圈中的总磁通量Φ也必保持不变.将式(11)代入式(8)可得

L1i1+M21i2=L1i0

移项后

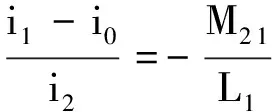
(12)

由此式可以看出，理想变压器接入负载后原线圈上的电流变化了(i1-i0)，这部分电流与i2成正比且同生同灭.所以，人们把它叫做负载电流“反射”到原线圈中的电流.等式右边的负号表示反射电流和负载电流产生的磁通相反，起平衡作用，这样才可以保证总磁通量Φ不变.

通常，在接近满载(即I2接近额定电流)时，反射电流(i1-i0)比励磁电流i0大得多，即i1-i0≈i1.因此，式(12)可近似写成

另外，在变压器无漏磁的情况下，可以证明

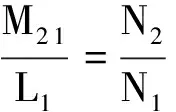
故，我们可以得到变压器的变流比公式

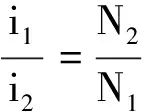
严格地讲，此中的i1，是理想变压器反射电流近似处理后的结果.并不是空载下的无功电流(励磁电流)i0,也不是此时原线圈上的总电流.

3 总结

回到开篇的问题，关于理想变压器原线圈上电流规律如下：

(1)空载电流I0≠0,但这个是无功电流，又称励磁电流.对理想变压器，I0→0.

参考文献

1 赵凯华,陈熙谋．电磁学．北京：高等教育出版社，1985

2 程守洙,江之永．普通物理学．北京：高等教育出版社，1998