基于EViews6.0软件下的普朗克常量测定
2012-01-23卢森杰马江剑芦立娟张艳春
卢森杰 马江剑 芦立娟 张艳春
(浙江海洋学院 浙江 舟山 316004)
大学物理实验中利用传统手工方法进行曲线拟合,其中的过程繁琐,精确度较低.本实验运用EViews 6.0①,输入数据后可得出高度拟合曲线,过程简单、快捷,得出的数据精确,再用C语言进行数据计算,使误差更小[1~10].
1 实验仪器
GD-Ⅲ型光电效应实验仪,电脑等.
2 实验原理
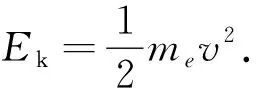
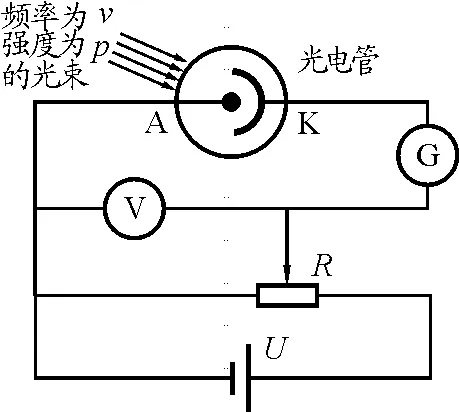
图1 光电效应原理图
(1)
上式称为爱因斯坦光电效应方程,式中h为普朗克常量,其公认值为6.626 075 5×10-34J·s;WS为受光线照射金属材料的光电子逸出功,是金属材料的固有属性,与入射光的频率无关;ν为入射光的频率;me为电子的质量;v为光电子逸出金属表面时的初速度[6].
如果阳极的电位比阴极低,即UAK为负值,它建立起来的电场对光电阴极逸出的光电子起减速作用,但也会落到阳极.随着阳极电位的进一步降低,到达阳极的光电子(光电流)将逐渐减小,直到阳极电位低于某一数值时,所有光电子都被抑制,不能到达阳极,此时光电流为零.这个相对于阴极为负值的阳极电位,被称为光电效应的截止电位,或称作截止电压,以US表示(这里的US代表截止电压的绝对值,为正值),如图2所示.

图2 伏安特性曲线
在光电效应的截止电位上,电子的初动能等于它克服电场力所做的功,即
可见电子的初动能和截止电压成正比.即
eUS=hν-WS
将上式变形得
(2)
(2) 拐点法求截止电压.光电管阳极反向光电流虽然较大,但在结构设计上,若是反向光电流能较快地饱和,则伏安特性曲线在反向电流进入饱和段后有着明显的拐点,如图2所示,拐点US即为截止电压[1].
(3)普朗克常量的数据处理原理.将实验数据用EViews 6.0软件进行伏安特性曲线的高度拟合,再在伏安特性曲线上利用拐点法求截止电压.将求出的频率和截止电压再次利用EViews 6.0软件画出回归直线并得到直线斜率k,再用h=ek(e=1.6×10-19C),最后求出h.
(4)普朗克常量不确定度的数据处理原理.利用Excel选4个空格→fx→统计→Linest(双击) →分别在表格最上的1,2两行中,填入原始数据(截止电压、频率);在3,4两行中,分别填入true,true→(Ctrl+Shift+Enter),则第一列第一行为斜率拟合值,第一列第二行为斜率拟合不确定度,再用Δh=eΔk求出Δh.
(5)利用C语言编程,自动计算出普朗克常量、不确定度和百分差[9].
3 方案设计
(1)测量光电管的伏安特性曲线.让光出射孔对准暗盒窗口,除去物镜盖,调节“电压调节”旋钮从-3.00 V或+3.00 V开始,缓慢增加,先粗测一遍,观察不同滤色片下的电流变化情况、电流明显变化的电压值以及饱和电流值.然后,从短波长起小心地逐次换上滤色片,仔细记录不同频率入射光照射下的光电流(在电流明显变化处多取几个数据)和相应的电压值.
(2)将实验数据用EViews 6.0软件高度拟合出伏安特性曲线方法如下.
下载软件并打开,新建一个变量,选择变量类型为其他,变量1~10,然后点击OK.建立一个空的变量,再输入数据,最后得到数据组.以图的形式打开一组电压-电流数据,出现一个对话框,点击左上方的View,选择Grope,出现Graph Options对话框,在Specifi栏选择Scatter,并在Fit lines栏中选择Nearest Neighbor Fit,然后点击“确定”.出现伏安特性曲线图.
(3)求回归直线方法同上,当出现Graph Options对话框时,在Specifi栏选择Scatter,并在Fit lines栏中选择Regression Line, 然后点击“确定”.得到回归直线图.从图中看到斜率.
4 实验数据及图线
(1)斜率的数据处理

表1 伏安特性曲线实验数据 (距离L=20.00 cm 光栏孔径为8 mm)
表2频率和截止电压(距离L=20.00 cm光栏孔径为8 mm )

波长/nm365405436546577h/×10-34 J·sE/%频率/×10-14Hz8.227.416.885.495.20US/V-1.66-1.24-1.07-0.53-0.386.55±0.251.2
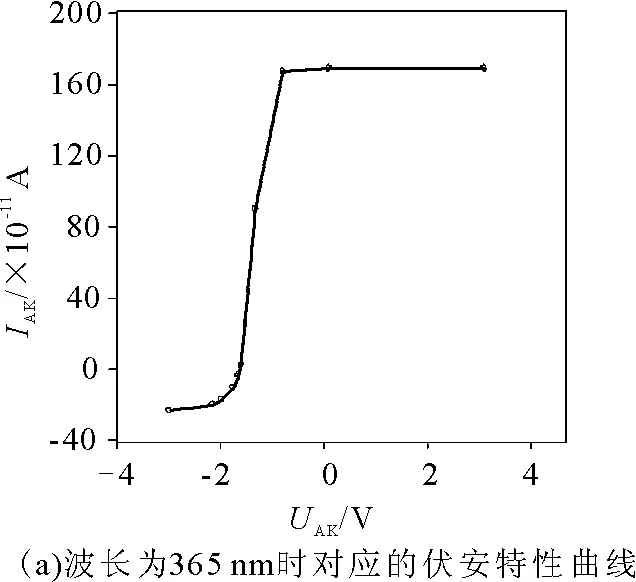

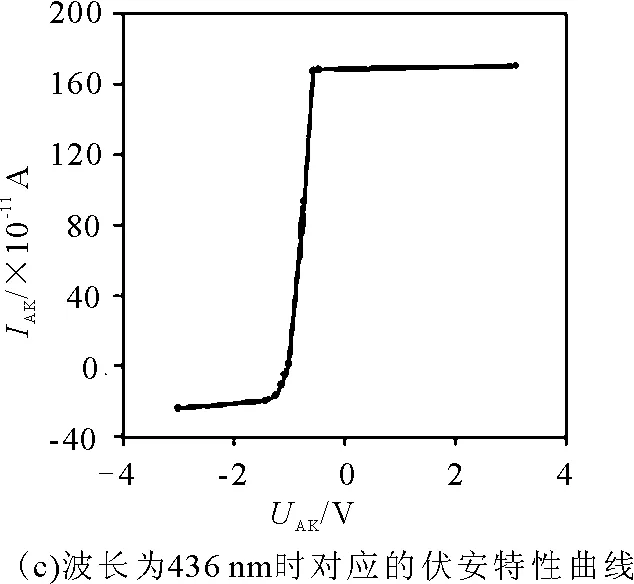


图3 用EViews 6.0软件进行高度拟合的伏安特性曲线
(2)斜率不确定度的数据处理
根据以上结果,由普朗克常量不确定的数据处理原理可得不确定度值为0.015 442.
(3)用C语言进行数据处理得普朗克常量、普朗克常量不确定度和百分差分别为h=6.55×10-34J·s,Δh=0.25×10-34J·s,E=-0.012 368.
5 实验结果讨论及分析
(1)本实验通过EViews6.0软件进行曲线拟合和运算,再利用C语言进行编程并自动运算,从结果h=(6.55±0.25)×10-34J·s,E=-1.2%,看出误差很小,证明了此软件的可行性.此软件在保证精确实验结果的同时简化了数据处理过程,为计算复杂数据提供了快速、准确的途径.


图4 Excel和EViews 6.0软件分别拟合回归直线及斜率
(2)用Excel和EViews6.0求得的斜率基本相同,但后者拟合的曲线比较光滑,截止电压取值比较方便.
综上,经过本次实验,测得了测普朗克常量.最终证明了EViews6.0软件进行数据处理的可行性. 为我们提供了处理数据的另一种新方法,提高了实验效率.
参考文献
1 吴泳华. 近代物理实验.北京:中国科技大学出版社,1995
2 周世勋. 量子力学 .北京: 高等教育出版社, 1979
3 陈泽民. 近代物理与高新技术物理基础 . 北京: 清华大学出版社, 2001
4 张社奇.高等学校新世纪系列教程.基础物理学.北京: 科学出版社,2001
5 (英)彼得·迈克尔,哈曼著.龚少明译.19 世纪物理学概念的发展——能量、力和物质.上海:复旦大学出版社,2000.2
6 竺江峰,芦立娟,鲁晓东.大学物理实验.北京:中国科学技术出版社,2005.212~219
7 赵青生,等主编. 大学物理实验. 北京:中国科技大学出版社, 1993
8 章佳伟,殷士龙.在光电效应实验中用曲率法测普朗克常量.物理实验,1980,23(11):42~44
9 高禹,冯相忠.C语言程序设计(第二版).北京:中国农业大学出版社,2010.1
10 张杰. 普朗克常数的测量和作图误差分析.物理实验,1998(03)
