圆锥摆模型的横向拓展
2012-01-23满孝旭
满孝旭
(枣庄市第三中学 山东 枣庄 277100)
通过平时的教学,笔者发现对于习题,学生总是教师讲过哪些题目就会哪些题目,而对于一些变形的题目则找不出思路,不知如何下手.再者,教师在平时的教学中经常给学生说要学会思考,要触类旁通,可学生还是不知道该怎么办.实际上,在教学过程中,我们应教会学生怎么去触类旁通.笔者以圆锥摆模型为例谈谈如何将基本模型横向拓展.
1 圆锥摆模型
小球的质量为m,通过质量不计的细绳悬挂于O点.小球摆动后细线与竖直方向成θ角且小球在水平面内做匀速圆周运动,半径为R(因小球与细绳摆动后形成一个圆锥形,故称之为圆锥摆).
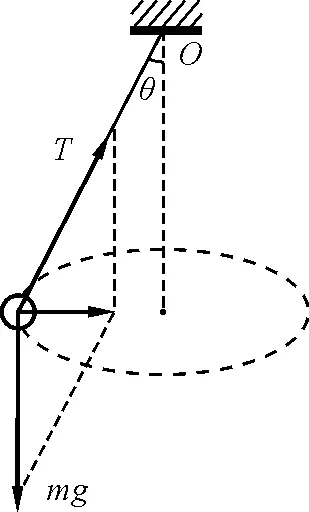
图1
小球在水平面内做匀速圆周运动,加速度必定指向圆心(合力指向圆心),又因为是匀速圆周运动,合力提供向心力.依据牛顿第二定律,对摆球受力分析(图1),得
F合=F向
F合=mgtanθ
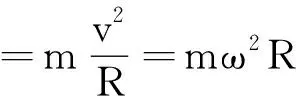
即
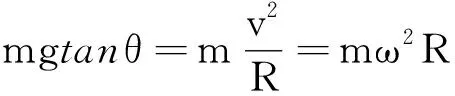
小结:问题的关键在于合力指向圆心,合力等于向心力.
2 拓展
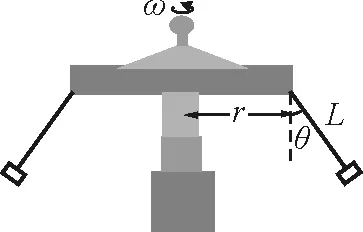
图2
【例1】有一种叫“飞椅”的游乐项目,示意图如图2所示,长为L的钢绳一端系着座椅,另一端固定在半径为r的水平转盘边缘,转盘可绕穿过其中心的竖直轴转动.当转盘以角速度ω匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向的夹角为θ.不计钢绳的重力,求转盘转动的角速度ω与夹角θ的关系.
分析:此题是一个很简单的圆锥摆模型的拓展,解决的办法还是先进行受力分析,然后得到方程F合=F向,即物体所受合力等于向心力.不同的是向心力表达式中的半径应表示为
R=r+Lsinθ
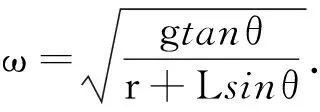
【例2】两个质量相同的小球甲和乙,用等长的不计质量的细绳悬挂于O点,且两球均在水平面内做匀速圆周运动,如图3所示.甲运动的半径比乙的大(甲在乙的上方),则
A.甲受到的向心力比乙的大
B.乙受到的向心力比甲的大
C.甲的角速度比乙的大
D.乙的角速度比甲的大
分析:读完此题后很多学生很快就能分析出A,B两个选项.设两绳子与竖直方向的夹角分别为θ甲和θ乙,由题意知,θ甲>θ乙,因
F合=mgtanθ=F向

图3
得甲受到的向心力大于乙受到的向心力.但到了后两个选项的时候就不知如何分析了.实际上基本思路没有变.用角速度表示出向心力,得方程
mgtanθ=mω2R
分析方程发现θ,ω,R三个量都不一样,根本判断不出角速度的大小.这时可能部分学生会选择放弃.但再读一遍题会发现,题目中还有一个条件,两绳长度一样没用上.由此,自然会想到用绳长表示半径,得方程
mgtanθ=mω2Lsinθ
化简得
因θ甲>θ乙,很明显甲的角速度比乙的大.
答案:选项A,C.
【例3】两个质量相同的小球丙、丁,在同一水平面内做匀速圆周运动,悬点相同.如图4所示,丙运动的半径比丁的大,则
A.丙受到的向心力比丁的大
B.丁受到的向心力比丙的大
C.丙的角速度比丁的大
D.丁的角速度比丙的大
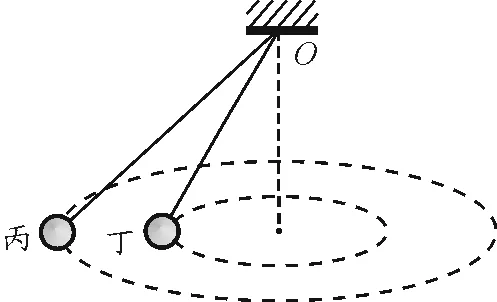
图4
分析:有了上一道题做铺垫,这道题就容易多了.只不过在分析角速度时要用高度来表示丙、丁两个小球做圆周运动的半径,因为题目中说两个小球在同一水平面内做匀速圆周运动.具体解析过程这里不再赘述.
答案:选项A.
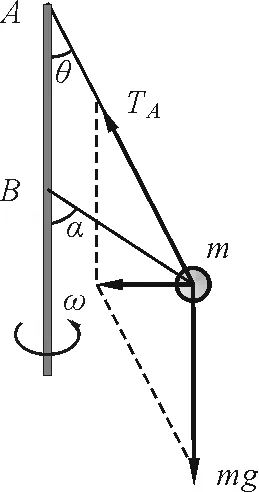
图5
【例4】如图5所示,两绳一端系一质量m=0.1 kg的小球,另一端分别固定于轴的A,B两处.上面绳长l=2 m,两绳拉直时与轴的夹角分别为30°和60°,问球的角速度在什么范围内两绳始终有张力?
分析:设两细绳都拉直时,A,B绳的拉力分别为TA,TB.小球的质量为m,A绳与竖直方向的夹角为θ=30°,B绳与竖直方向的夹角为α=60°.
当角速度无限小时B绳就不是拉直状态了,故角速度取最小值时B绳拉直且恰无拉力.受力分析如图5所示,可得
得
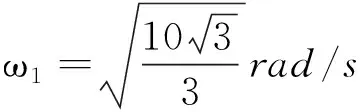
当角速度无限大时A绳就不是拉直状态了,故角速度取最大值时A绳伸直且恰无拉力.同理可得
得
所以,两绳始终有张力,角速度的范围是
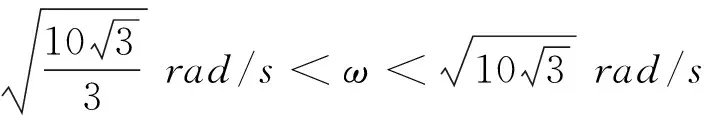
小结:该类问题无论怎么拓展,解题的基本思想不会变,即合力提供向心力,只不过向心力的表达式要根据题意表示出来.
3 结束语
其实学习物理并不难,很多学生之所以认为物理难学,实际是没有把握住物理规律或者是对物理规律的理解不透彻.所以,在以后的物理学习中要特别注意对物理规律的理解,对基本模型和一些拓展理解透彻,才能举一反三.
