对一道运动学问题的深度思考
2012-01-23何勇
何 勇
(新疆兵团二中 新疆 乌鲁木齐 830002)
在“乌鲁木齐地区2011年高三年级第一次诊断性测试”中,一道考查学生关于运动学的选择题引起了笔者的思考.
【例1】某兴趣小组作如下实验:将3块外形相同的正方形木板甲、乙、丙,如图1拼接起来放在水平地面上.一可视为质点的小物体以一定的初速度依次滑过3块木板.小物体与3块木板的动摩擦因数之比为μ甲∶μ乙∶μ丙=1∶2∶3;如果小物体每次初速度相同,3块木板的顺序可任意拼接.若要小物体滑过3块木板所用的时间最短,小物体依次滑过三块木板的顺序为
A.甲、乙、丙 B.丙、乙、甲
C.乙、甲、丙 D.乙、丙、甲
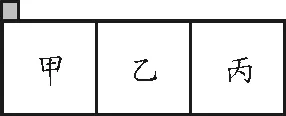
图1
首先,本道题应该保证“木板在地面上静止不动”,这一点题目表述含糊不清.3块木块拼接起来,成为一个长是宽的3倍的矩形.小物体运动的轨迹平行于矩形的长边.
接下来,对甲、乙、丙如果在地面上不滑动,进行以下分析.
设每块木板的宽度均为L,小物体滑上木板的初速度为v0,离开时速度为vt,小物体在木板上滑动根据动能定理可得
-μ甲mgL-μ乙mgL-μ丙mgL=
根据上式可知:小物块以相同初速度v0从一端滑上木板,离开时末速度vt也一定相等.
1 对两个木板运动的分析:令μ甲<μ乙
(1)图像法
由于滑块在每块木板上都做匀减速运动,在保证相同的初速度下,且每块木板上滑行的位移相同,则末速度必然相同,可画出图2(a)、(b)对应的v-t图,如图2(c).
根据v-t图可知,按图2(a)运动的时间ta较图2(b)运动的时间tb要短.

图2
(2)平均速度法
设物体滑到中点的速度为v,则其从左端滑到右端,有
t=t1+t2
根据以上两式可知:要想使物体在物块上运动的时间最短,必须保证小物体运动到中间的速度较大;故图2(a)较图2(b)方式的时间要短.
通过以上两种方法都可以确定先滑过光滑面,后滑过粗糙面的时间较短.同时可以推广到3块木板很容易分析得出结论:依次滑过甲、乙、丙的时间最短,选项A正确.
2 推广到在多块木块的减速运动
在分析之前不妨先来看一个相关问题.
【例2】如图3,一个木块滑上一个粗糙程度不均匀的固定水平木板,如果木板从A端至B端与滑块的动摩擦因数连续增大.试判断滑块从哪一端滑上木板的时间较短?

图3
解析:设物体的初速度为v0,末速度为vt,摩擦力做功为Wf.
根据动能定理可得
经分析木块从甲端滑至B端和木块从B端滑至甲端,摩擦力做功相同,由上式可以得出,木块的末速度vt也相同,其运动的v-t图如图4所示.显而易见,tAB 图4 如果滑块与木板间各处的动摩擦因数不同,而木板可以无限分割并且可以任意拼接,当木板按照动摩擦因数从小到大的顺序排列时,滑块在木板上运动时间是最短时间吗? 构造模型:如图5所示,一个可视作质点的质量为m1的物块,滑上一个粗糙程度不同的木板. 图5 问题分析:假设将AB之间粗糙水平面分成n段,其速度分别记作v1,v2,…,vj,vj+1,…,vn,vn+1,在可以看成相等很小位移Δl的动摩擦因数分别记作μ1,μ2,…,μj,μj+1,…,μn-1,μn,设{μn}为任意排列. 现将其中任意一段当做匀减速直线运动来处理,可以列出方程组 将以上各方程组累加可得 对于其中任意一段Δl的运动时间 所以,滑块从A端滑到B端的总时间 μ1<μ2<…<μn-1<μn μ1>μ2>…>μn-1>μn 探究结论:一个物体从光滑端向粗糙端滑行的时间最短,从粗糙端向光滑端滑行的时间最长. 现在,再来看物块滑过3个木板按甲、乙、丙拼接,小物体滑过3块木板所用的时间最短;物块滑过3个木板按丙、乙、甲拼接,小物体滑过3块木板所用的时间最长就显而易见了.



