发展性教学中渗透物理学史的尝试*①——“库仑定律”的案例教学

周诗文 彭玉霞

(海南大学材料与化工学院 海南 海口 570228)

发展性课堂教学的理念提倡在教学的过程中,不但要重视“知识技能”的教学，而且要关注对“人文精神”、“创新精神”的教育与传承，促使学生从“知识灌输”的“容器”转变为“知识意义”的主动“建构者”．这种教学理念有利于重新确立人文精神和创新精神的理性地位，让学生在获得知识、能力的过程中，赢得人格和尊严，并形成持久的学习和工作动力，以及强烈的研究志趣．笔者运用发展性教学的理念，充分挖掘物理学史的教育功能，以“库仑定律”为案例开展了探索性的研究．

1 案例教学的设计思想

库仑定律的发展和建立过程中，蕴含着经典的人文精神和创新思维素材．教师可以运用这些素材创设教学情境，引导学生经历一定的历史“重演”过程，从而训练和提高其创新思维能力与实验设计能力，培养其热爱科学的情怀．基于这种贯彻发展性课堂教学的理念，笔者以“历史背景简介-科学猜想-历史实验介绍-模拟实验验证-定律的理解” 为教学的主线，采用科学探究、自主学习与交流相结合的模式展开教学．

2 案例的教学过程

2.1 历史背景简介

1766年英国化学家和物理学家普列斯特利(J.Pristley)利用带电金属腔实验[1](图1)，发现腔内壁无电荷，且对置于其内的电荷明显地没有作用力．由此他提出猜想：静电力与距离的平方成反比．我们如何理解这一猜想呢？

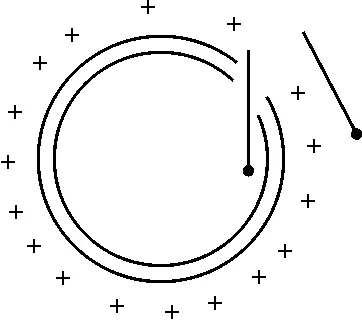
图1 带电金属腔对电荷的作用

2.2 猜想与假设

(1)现象与联想

由图1所示的实验现象，联想到万有引力的类似现象，即放在均质球壳内的物质不会受到来自壳体本身物质的作用力，而当物体放在壳外时，两者之间却存在引力作用．后一情形是显然的；前一情形，可从以下分析得出．

(2)推证

如图2，设一质量为m0的质点，置于匀质薄球壳(面密度为σ)P处，过P作一对小锥体，两锥体的“对顶立体角”为dΩ，锥体与球壳相交所截得的面元分别为dS1，dS2，自点P至两面元的距离分别为r1，r2．P处质点受到dS1，dS2上的质元的万有引力分别为

由立体角的定义

根据几何关系r1与(-r2)平行，得

θ=(dS1,r1)=(dS2,r2)

由以上三式可得

dF2=-dF1

故质元m0所受合力

F=∬S(dF1+dF2)=0

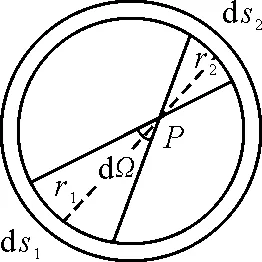
图2 均质球面内无引力

(3)类比及猜想

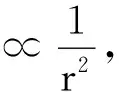
库仑定律相对应地也有属性：两电荷量分别为q1，q2，它们的间距r，两者之间作用力F电，带电金属腔对腔内的带电体无电力作用，对腔外的带电体有电力作用．

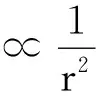
教师指出，类比得出的结论可能存在局限性，其正确与否还须用实验来验证．

2.3 历史实验介绍

2.3.1 第一小组的学习报告与讨论

(1)卡文迪什-麦克斯韦的“示零”实验介绍[2]

1773年卡文迪什的验证实验：把一个带电导体球放在一个不带电的空心导体球壳内(球壳由两个金属半球拼成)，接着通过外球壳上的一小孔，用细导线将内球与外球壳连接起来，经过一段时间，打开空心球壳，取出内球，使之与验电器相连，检测内球是否带电．

此实验的设计思想是：由测量力转化为测残留电荷，即如果实验测得内球不带电，就可间接确定静电力的大小符合距离平方反比律．考虑到测量误差，实验结果的形式可拟写为f∝r-2±δ，并且δ越小，内表面电荷就越小．卡文迪什根据检测内球所残留的电荷数量，推算出δ应满足δ≤2×10-2．由于δ很小，他推断静电力的大小应符合距离平方反比律．

1873年麦克斯韦进一步改进了上述实验，把测量空腔导体内球的电量改为测量其电位．麦克斯韦把一导体球同心地置于另一导体球壳内，并用短导线使两导体球相连，将外球与带电的莱顿瓶相接，充电到一定电位．充电完毕后，撤去两球间的短导线，并使外球接地，即使之放电．再用静电计通过外球上的一小孔，探入内球，测量内球电位．观察结果发现，内球的电位没有任何微弱的变化，即内球的电位保持为零．麦克斯韦由内球的这种电位 “示零”结果，便间接地证明了静电力符合距离平方反比律，而且实验精度提高了二个数量级．

(2)问题讨论与交流

问题与思考：卡文迪什的“示零”实验、麦克斯韦的“示零”实验、普列斯特利的实验，这3个实验的思想是一脉相承的吗？为什么说若检测到球壳内壁或内球所带的电荷为零，就间接证明了“静电力与距离平方成反比”的关系？

学生对问题一的主要观点：上述3个实验的基本实验思想是一脉相承的．因为卡文迪什的实验与麦克斯韦的实验要得到“示零”的结果，其内球都必定不能有净余电荷存在；而此时这2个实验都用短导线使内球与外球壳相连，这种实验操作的结果等效于内球为球壳的内壁；普列斯特利正是从金属腔的内表面没有电荷的现象，而提出静电力与距离平方成反比的猜想；所以3个实验的基本思想是一致的．

学生对问题二的主要观点：为论证问题二，需要利用猜想中的推证结论——当静电力符合距离平方反比律时，带电金属腔对腔内的带电体无电力作用，对腔外的带电体有电力作用．

首先，对于带电金属球壳，若内壁也带有净余电荷，则根据上述结论可知：内壁上的每个电荷所受静电力的合力只来自内壁上的其他电荷对它的排斥力，其合力的方向指向球壳的外法向；考虑到内壁之外的正电荷虽然也可能受到静电力的作用，但不会移动，因而对内壁之外的元电荷可只分析电子的受力情况，这些电子所受的力来自于内壁上所有净余电荷的斥力或引力作用或外壁对它的弹力(根据电荷分布的球对称性，壳内其余电荷对这些电子的作用力的合力应为零)．当内壁带负电荷(即电子)时，这些电子及内壁之外的电子会因斥力作用而向球壳外壁方向移动，直至内壁没有净余电荷为止．否则，只要内壁上有残余电荷，则总会有电子因受力而移动．同理，当内壁带正电荷时，就会有电子从内壁之外向内壁移动，直至内壁显中性为止．

其次，对卡文迪什-麦克斯韦“示零”实验，可进行类似分析：只要内球带有净余电荷，系统中就总有电子发生移动，直至内球呈中性为止．其实，此时内球就相当于球壳的内壁．

在推导上述内壁或内球所带电荷的“示零”过程中，已利用了“静电力与距离平方成反比”的假设．故若实验检测到内球不带电荷，便间接证明了假设成立的正确性．

教师小结：大家利用球壳具有球对称性，由此来分析其电子的受力情况，非常不错！等我们学了高斯定理后，可结合该定理用更简单的方法来论证．

2.3.2 第二小组的学习报告---库仑的扭秤实验[3]

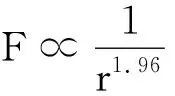
2.4 “电摆”模拟实验

问题：刚才有同学提到库仑还设计了“电摆”实验，设计“电摆”实验的目的是什么?

问题提出后学生们立即指出用扭秤不能测量异号电荷间的引力，并且说出了如下理由：

异号电荷之间的相互作用力为引力，而扭秤中的金属丝所对应的扭转回复力矩，仅与扭转角度的一次方成比例，因而扭秤不能稳定工作．当两带电球相距较远时，引力较小，测量误差将很大；当相距较近时，扭秤会出现左右摇摆，两球也往往会相碰、接触而发生电荷中和现象，使实验无法进行下去．

思考：如何理解“电摆”实验的原理？

教师激励学生进行联想、类比推理，学生由“愤悱”状态，找到了利用重力单摆来推理类比的出路．以下是学生提出的“电摆”实验原理：

教师赞赏地指出，学生们的实验思想与库仑当时的想法完全相同；同时要求学生下次课在实验室进行模拟实验并组织各小组同学以PPT的形式，将实验成果进行展示和交流．

2.5 库仑定律的理解与应用

(1)库仑定律的表述与理解

库仑定律的数学形式

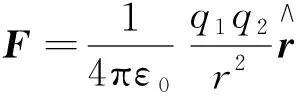
教师组织学生对定律中涉及的力的方向、定律成立的条件、适用的范围等问题进行讨论，并归纳得出如下结论.

结论一：必须通过实验与思维才能得到上述公式．如力的方向，分析点电荷的受力可知，其相互作用力只能沿两个点电荷的连线，否则空间旋转180°就会失去相应的对称性．

结论二：定律成立条件——静止、真空、点电荷．

1)“静止”条件是指发生相互作用的点电荷相对于观察者是静止的．

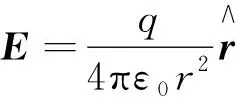
2)真空条件指发生相互作用的电荷处于真空．

引入这一条件的目的在于：免除其他电荷的影响，使两个点电荷只受到对方的作用力．

那么，如果真空条件破坏，结果将如何呢？

师生共同探讨得出：此时总作用力比真空时复杂些，两电荷各自所受到的作用力不仅只是来自对方电荷的作用，还会来自所处介质中其他电荷对它们所施加的电力作用．但根据力的独立性原理可知，这两个点电荷之间的力仍遵循库仑定律．因此库仑定律也适用处于介质、导体中的电荷之间的作用力，只是此时电荷所受的总静电作用力的大小要进行一定的修正．

3)点电荷的条件是指对于所研究的问题，带电体的形状、大小以及电荷分布等情况几乎可以忽略．此时，便可把带电体作为没有大小、形状，但带有一定电荷的几何点．

其实，点电荷的条件也可以不提，因为连续的带电体在数学上总可无限分割为无穷多个点电荷的集合，再根据叠加原理，就可以利用库仑定律并进行相应的积分运算，求得带电体间的相互作用力．

结论三：适用范围.

教师指出在现有实验条件下，以及已有的研究表明，库仑定律对于原子核尺度、地球物理尺度、天体物理、空间物理使用时都还没有发现不合理的问题，通常认为库仑定律的适用范围在10-13cm到若干千米的范围内，也有文献报道可以到109m之间[4]．

(2)库仑定律的理论地位和现代含义

随着科学的发展，库仑定律不断被赋予新的内涵．例如，在原子结构、分子结构、固体液体的结构，化学作用的微观本质等方面都与电磁力有关，其中主要的部分是库仑力．同时，库仑定律的平方反比关系的成立与否，对于现有的物理理论起着重要的检验作用．例如，光子的静质量是否为零与库仑定律是否满足平方反比律密切相关，这是因为电磁相互作用是由荷电粒子间交换(虚)光子而实现的．现代物理已经证明，若光子的静质量为零，则静电力严格遵循距离平方反比规律．反之，则不成立，由此将带来一些原则性的问题．如，直接导致电磁场的规范不变性不再成立；电荷守恒定律被破坏；电磁波在真空中也发生色散，从而破坏光速不变原理．凡此种种，都将是动摇物理基础的问题．

由此可见，库仑定律的精确验证，在现代物理中有着重要的理论地位与实践意义．

3 案例分析

本案例按照发展性课堂教学的理念，采取科学探究式教学模式，围绕库仑定律的建立过程和正确理解，有机地结合物理学史资源,展开了极富构建意义的教学活动．研究表明，发展性物理课堂教学中渗透物理学史的教学具有极强的操作性，其教学过程是师生共同经历发现问题、设计和实施研讨方案的过程．这种平等的探讨与交流、合作和分工的教学方式非常自然地调动学生自觉地参与到知识的产生和发展过程中来．显然，通过这种发展性教学可以同时实现新课程的“三维”教学目标，尤其是学生的创新思维能力、科学精神和人文情怀，以及学习与交流等重要能力和品质都得到了不同程度的培养和熏陶．

参考文献

1 郭奕玲,沈慧君. 物理学史. 北京: 清华大学出版社,1993.221～222

2 倪光炯，等.改变世界的物理学(第二版).上海: 复旦大学出版社，1999.9～16

3 郭奕玲,沈慧君.近代物理著名实验简介. 济南:山东教育出版社，2001.241～249

4 徐游.电磁学(第二版).北京:科学出版社,2004.233～235