外压圆锥壳开孔应力集中系数分析

，

(1.武汉船舶职业技术学院 船舶工程系，武汉 430050；2.武汉理工大学 交通学院，武汉 430063)

圆锥壳开孔与圆柱壳开孔一样具有重要的工程意义，由于圆锥母线与中心线的夹角，其开孔的力学特性比圆柱开孔复杂。目前，关于圆柱壳开孔的研究已比较成熟，关于在圆锥壳上开孔，具有代表性的研究是圆锥壳的精确解与等效圆柱壳的解的比较[1]及讨论圆柱壳曲率半径保持恒定，而圆锥壳的半径是一个变化量，且是一非圆孔[2]。对圆锥壳开孔的影响因素比较多，力学规律比较复杂。本文旨在分析圆锥壳开孔大小、锥角等因素对应力集中系数及应力分布规律的影响，并分析围栏加强对降低应力集中系数的影响，提出圆锥壳开孔的加强措施。

为了适应特定环境的需要，圆锥壳开孔中心线几乎可以与锥壳中心线平行，而圆柱壳是无法实现的。在外压作用下，圆锥壳开孔会导致应力集中，但关于应力集中的特点以及应力集中的量值均未见系统的研究。本文根据圆锥壳的开孔角度，将其分为三类，采用有限元方法，以锥角为变量，对圆锥壳开孔进行系列计算，分析应力集中系数的规律，为圆锥壳开孔设计提供理论依据。

1 圆锥壳开孔形式及参数定义

与圆柱壳一样，圆锥开孔也分为正交和斜交开孔两种形式，开孔形式及参数见图1。然而圆锥壳正交开孔的定义没有圆柱壳那样明确。如果参照圆柱正交开孔[3]的定义，圆锥正交开孔指的是开孔中心线垂直于锥壳中心线，即α=90°(见图1)。由于圆柱壳母线同中心线平行，因此圆柱壳正交孔实际上是垂直于壳体的，根据这一特性，圆锥壳的正交开孔也可定义为与圆锥壳母线垂直的开孔，即α=90°。以后一种形式作为正交孔的定义，前一种开孔作为一种典型的开孔形式。

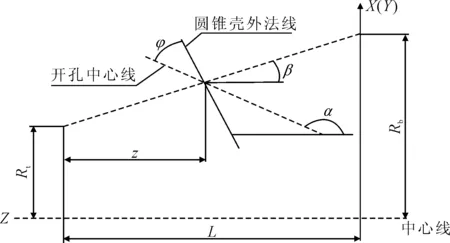
图1 圆锥壳开孔形式及参数

为了表述应力集中的大小，定义应力集中系数k为

k=σ/σn

(1)

式中：σ——开孔处的最大应力;

σn——开孔中心的名义应力，σn=PRZ/t。

2 有限元模型的建立

主要分析理想圆锥壳开孔应力集中系数的大小及应力分布的规律，不对圆锥壳开孔结构进行强度校核，因此结构的计算载荷采用单位载荷，即计算压力p=1 MPa。

圆锥壳开孔有限元模型采用shell63单元，开孔区域网格划分较小，单元最小尺寸不超过30 mm，并向四周过渡；对于大倾角开孔，开孔局部区域采用solid45单元。模型小端设置封板，大端刚性固定，小端仅留轴向以及转动自由度。

3 锥角对应力集中系数的影响

根据变量转换公式[4]，通过量级分析，略去h/R量级的小量，从而将圆锥壳有矩问题求解的基本微分方程转换成一个二阶复常系数的常微分方程式。计算时保持开孔中心处圆锥壳截面半径恒定，通过改变锥壳大小端半径控制锥角的大小。根据开孔中心线与锥壳的关系将开孔分为三类。

1) 第一类开孔，α=90°，开孔中心线与圆锥壳中心线垂直；

2) 第二类开孔，α-β=90°，开孔中心线垂直于圆锥壳曲面；

3) 第三类为大倾角开孔，一般取α=150～180°，中心线与锥壳母线成小夹角。

计算作以下假定：锥段长度L=5 000 mm，开孔半径a=400 mm，开孔中心位置锥壳半径RZ=3 000 mm，开孔中心位于锥壳段中心，即z=L/2，锥壳厚度t=20 mm，其余参数根据已知参数求得，计算结果见表1，孔边壳板的应力分布见图2～5。

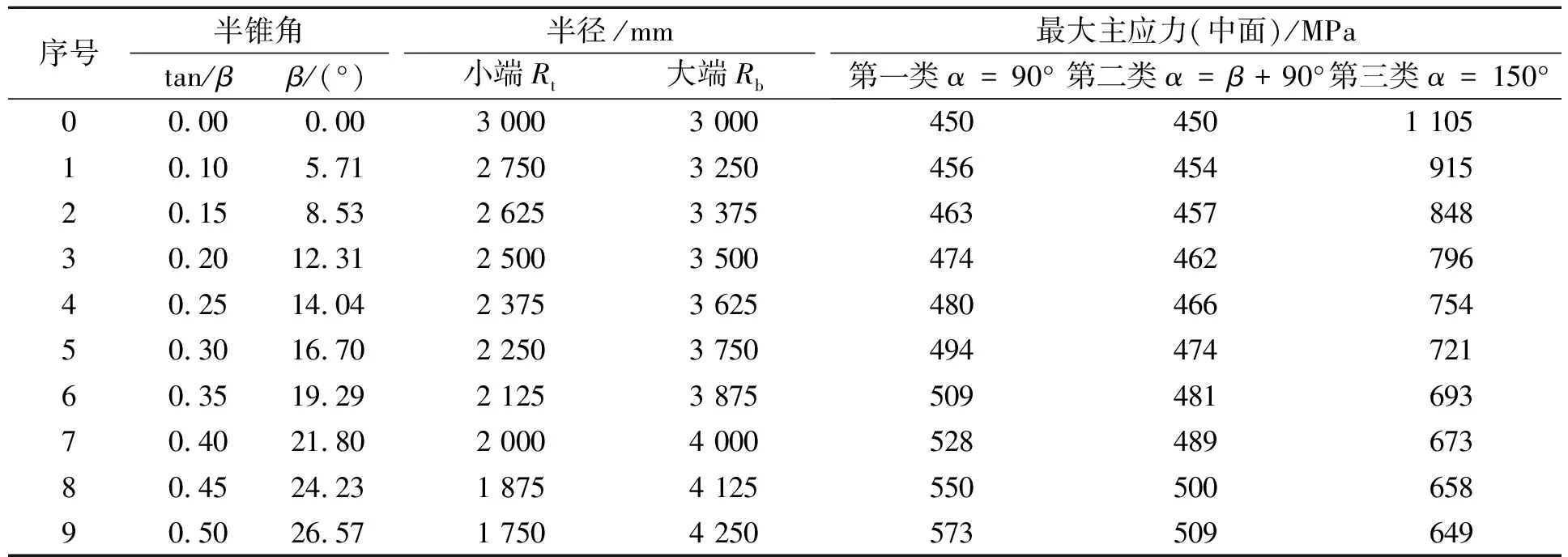
表1 不同锥角情况下孔边壳板最大主应力

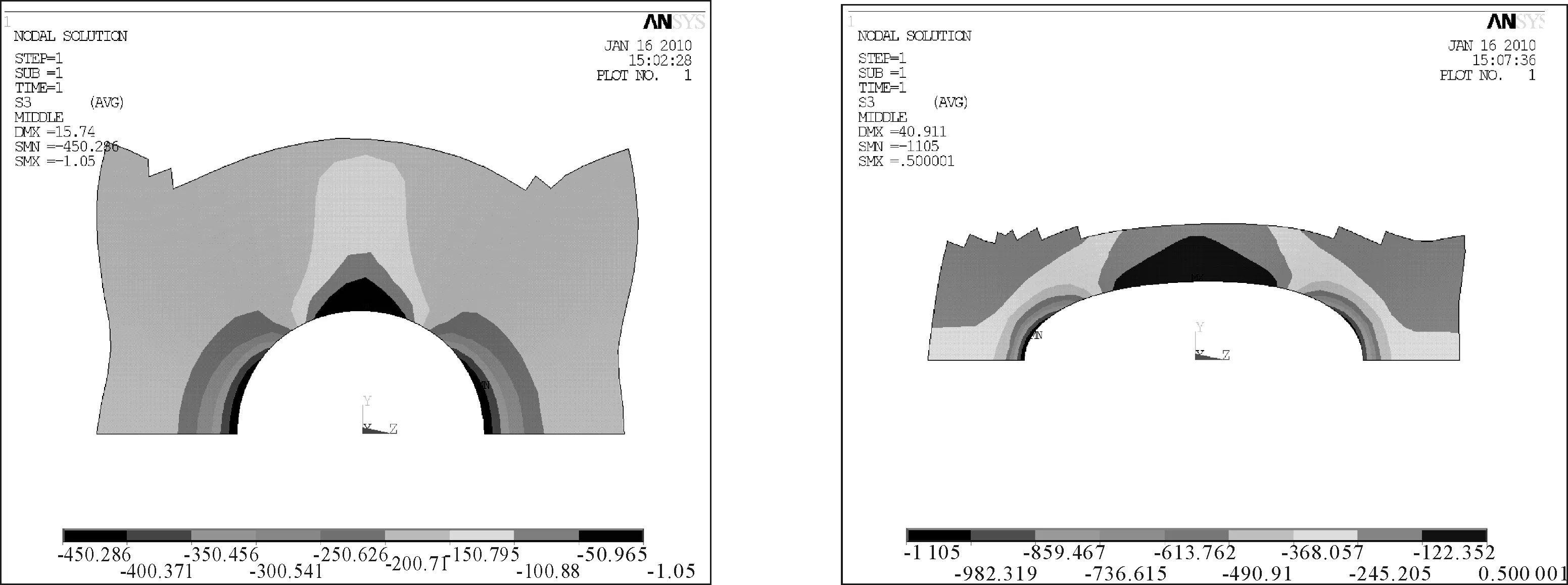
图2 圆柱壳正交开孔孔边中面应力 图3 tanβ=0第三类开孔孔边中面应力

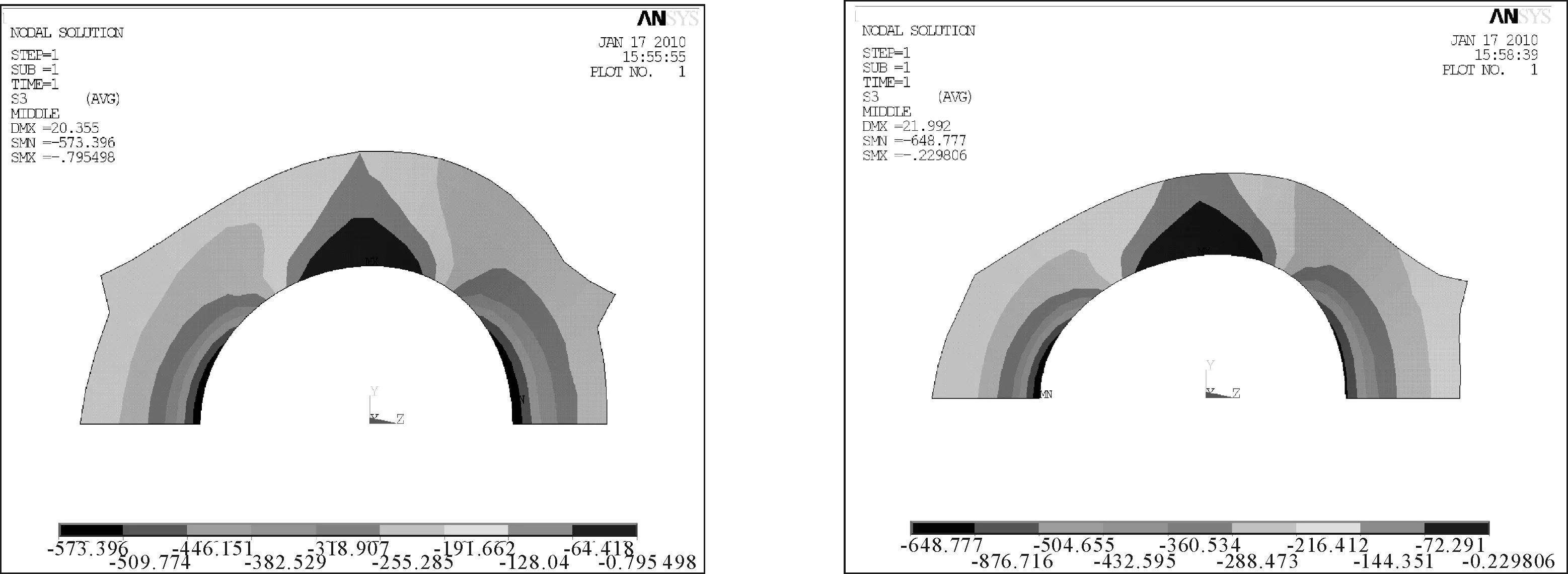
图4 tanβ=0.3第一类开孔孔边中面 图5 tanβ=0.3第三类开孔孔边中面应力

从表1可见，随着圆锥壳半锥角的增大，第一、二类开孔中面主应力逐步增大，其中第二类开孔主应力增加缓慢，而第三类开孔主应力减小，且减小的幅度随着半锥角的增大而变缓；第三类开孔的最大主应力明显高于第一、二类开孔。三类开孔中，第二类开孔孔边壳板主应力最低，第一类介于第二、三类之间。

通过上述分析发现，开孔应力的大小实际上与开孔的面积有较为直接的关系，由于第二类开孔中心线与壳板正交，因此开孔面积最小，且开孔面积几乎不变；而第一、三类开孔与壳板斜交，开孔面积较大，尤其是第三类大倾角开孔，当半锥角较小时，开孔面积较大，极端的当β=0(圆柱壳)时，开孔面积最大，应力也最大。

以圆锥壳壳板外法线方向作为0°角，将开孔中心线与外法线的夹角定义为新的开孔角度φ，φ=α-β-90°，相应的三类开孔的角度分别为：第一类φ=-β;第二类φ=0;第三类φ=-β+60°。根据新定义的开孔角，在不同半锥角情况下，孔边壳板的应力集中系数见表2。

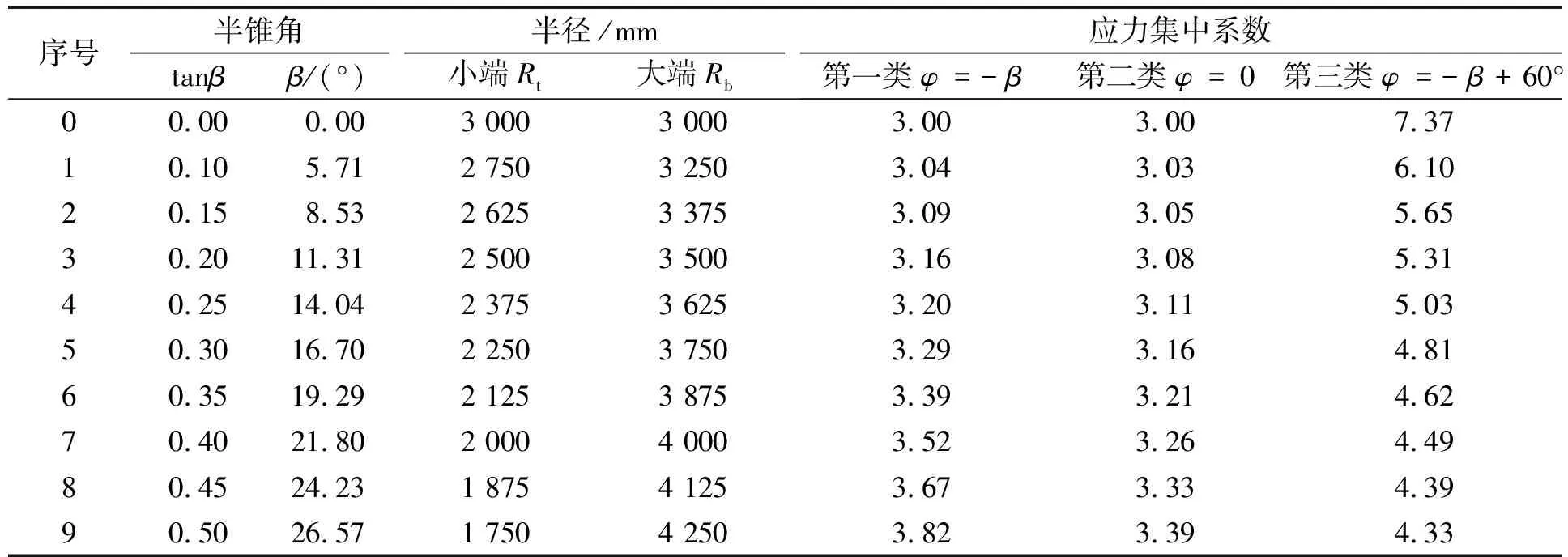
表2 不同锥角情况下孔边壳板应力集中系数

从孔边壳板的应力云图可以看出，应力集中发生在开孔前后端，第三类开孔的最大应力位于开孔后端，即圆锥壳直径较小的一端。开孔前后端曲率半径存在一定差异，靠大端的曲率半径大于小端的曲率半径。

4 结论

圆锥壳正交开孔的应力集中系数最小，大斜角开孔的应力集中系数明显高于正交开孔，实际应用时应严格控制开孔的偏斜角。文中仅讨论自由开孔的应力集中系数，其值均较高，但只要采取合理的加强措施，如围壁加强，可有效降低应力集中系数，满足工程要求。

[1] 崔维成,裴俊厚,张 伟.圆锥壳的精确解与等效圆柱壳的解的比较[J].船舶力学,2000,4(4):34-42.

[2] 刘殿魁,胡 超. 圆柱壳开孔的应力集中——非圆孔问题的一般解[J].应用数学和力学,1997,18(7):585-602.

[3] 徐秉汉,裴俊厚,朱邦俊.壳体开孔的理论与实验[M].北京:国防工业出版社,1987.

[4] 崔维成,裴俊厚,张 伟.具有薄壳理论同样精度的圆锥壳简化解[J].上海交通大学学报, 2002,36(1):125-128.