海洋工程结构物碰撞失效准则探讨
2012-01-22,
,
(德国劳氏船级社 未来船舶技术咨询,上海 200020)
在当今的非线性有限元模拟仿真领域,V-M等效应变εeff普遍地被用作为失效应变准则[1]
(1)
在动力显式分析中,程序按照增量理论计算单元的塑性应变,通过式(1)来衡量结构的变形是否超出了预设的范围,当应变超出了设定的失效应变值时,单元就会自动失效,不再参与有限元分析。该失效准则有两个显著的特点:①综合考虑的三个主应变对单元失效的影响;②由于Von-Mises应力和应变是从能量角度推导出来的,因此没有方向性,无法区分结构承受的载荷是拉应力还是压应力,当单元的V-M等效应变达到预设值时,单元就会失效。
由此可见,结构受拉还是受压对V-M等效应变准则是没有区别的,但是在实际工程中,结构受载形式的不同却会对其强度和稳性有着至关重要的影响。以单轴拉伸压缩试验为例,对于低碳钢这种弹塑性材料,其受拉时分为明显的弹性阶段、屈服阶段、强化阶段和颈缩阶段,其抗拉极限强度很容易测出。而当其受压时,试件越压越扁,曲线不断上升,得不到材料的抗压极限强度。对于铸铁这种典型的脆性材料,其抗压极限是抗拉极限的5~6倍。所以通常情况下钢材的破坏是因为受拉导致的,大部分情况下受压只会导致结构的失稳。因此,V-M失效准则不能真实地描述复杂应力状态下的结构失效。为此,考虑应用理论上可行的厚度应变准则来代替V-M失效准则。
1 有限元分析模型的选取和建立
1.1 模型选取
典型的船体舷侧结构板架或海洋平台结构板架见图1、2。

图1 船体舷侧结构

图2 典型船体板架结构
以板格为研究对象。当发生板平面法向载荷作用时,面板和上面的骨材会向内侧凹曲,板格两端会受到其它桁材和骨材的约束限制,不仅会发生转动,还会有向内侧的位移,其变形见图3。
故可以简单地将其视为两端弹性固定的简支梁。

图3 典型板格结构受外载变形
1.2 材料属性的定义
应用非线性有限元软件LS-DYNA进行模拟仿真。选取软件中的*MAT123作为材料模型,*MAT123是修改后的多线性弹塑性材料模型,可以单独设定材料达到屈服后的硬化过程曲线,见图4。除此之外,它也嵌入了应变率的影响。

图4 材料的真实应力应变关系曲线
*MAT123的最大特点是融合了三种失效准则——V-M等效应变失效准则、材料厚度方向应变失效准则以及最大主应变失效准则,通过对这三种失效准则进行搭配组合,可以找到一种能够更加精确描述材料失效准则的方案。
应用LS-DYNA软件作为分析工具,选取*MAT123为材料的本构模型。当结构受到冲击载荷时,结构各个部位的应变变化速率不同。此次模拟没有考虑应变率的影响。
由于非线性破坏计算涉及到结构的极端几何特性和材料特性,而且材料属性中的极端拉伸应力对结构的变形能有重要的影响。针对这种非线性模拟仿真,推荐使用材料的真实应力应变关系曲线。可以从拉伸试验获取该曲线,并通过公式(2)计算得到[2]。
σ=Cεn
(2)
式中:
进而,为了实现这样一个目标,不仅应当明确提倡理论的多元化,“当两个隐喻相互竞争并不断相映证可能的缺陷,这样就更有可能为学习者和教师提供更自由的和坚实的效果”[25];也应始终坚持自己的独立思考,而这事实上也正是何以特别强调“理论的实践性解读”的又一重要原因,即是应当通过积极的教学实践对相关理论的真理性做出必要的检验,并促使其不断完善和进一步发展.
n=ln(1+Ag)
(3)
(4)
其中:Ag——最大均匀应变;
Rm——极限拉伸应力。
Ag、Rm值都可以从拉伸试验中获得。德国劳氏船级社专家研究发现,当Rm为已知的时候,Ag可以通过公式(5)获得。
(5)
材料的真实应力、应变曲线关系见图5。

图5 材料的真实应力-应变关系曲线
2 选取不同失效准则时的非线性有限元模拟分析
2.1 V-M失效准则
首先应用V-M失效准则进行梁的弯曲模拟,由于只关注梁的破坏形式,并不关注能量的转化守恒,所以对梁跨中中性面上的3个节点设置速度,保证梁的跨中中性面3个节点以1 m/s的速度向下运动。梁的边界条件采用简支梁的形式,一端限制水平和垂向的位移,一端只限制垂向的位移,不限制转角。为了防止网格产生大变形而导致结果不准确,采用自适应网格技术。为了完全模拟出钢材的真实应力变化情况,采用德国劳氏船级社通过实验获得的钢材的真实应力应变关系曲线对材料的塑性硬化阶段进行描述。模拟过程中几个关键时刻的应力云图见图6。
从图6最后一幅图中可见,大约在模拟开始后的0.04 s时,梁跨中部分的顶部和底部的单元几乎同时失效破坏。说明模拟结果是梁跨中的上部和下部都同时破坏,而根据之前的叙述,钢材的受压极限远大于其受拉极限。真实情况是梁的跨中底部边缘首先破坏,其失效是由于其结构内部应力超过了结构本身的受拉承载极限,而模拟结果与真实实验结果明显不符,说明V-M失效准则有局限性。

图6 V-M失效应变下梁的应力云图变化过程
对梁结构进行受力与变形分析,选取跨中4个单元(505、506、350和349),见图7。
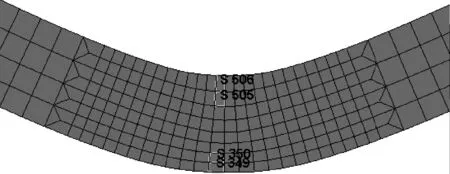
图7 失效单元位置及编号
图8是4个单元的V-M应力-时间变化曲线。可以看出在模拟开始后,结构的应力呈现出明显的线性阶段,这是由于此时单元内部的应力还没有达到钢材的比例极限。随后钢材进入了塑性硬化阶段,约在0.040 s的时刻,A、B、C和D曲线在很短时间内迅速下降,这代表4个单元几乎同时发生破坏失效。
从应变-时间关系曲线(见图9)中可见,在刚开始0.001 s内,钢材处于弹性阶段,由于钢材本身弹性模量很大,所以其应变维持在一个较小的增长范围。屈服阶段大约维持了0.002 s,所以此时的应变没有发生变化,维持在0.0025左右。
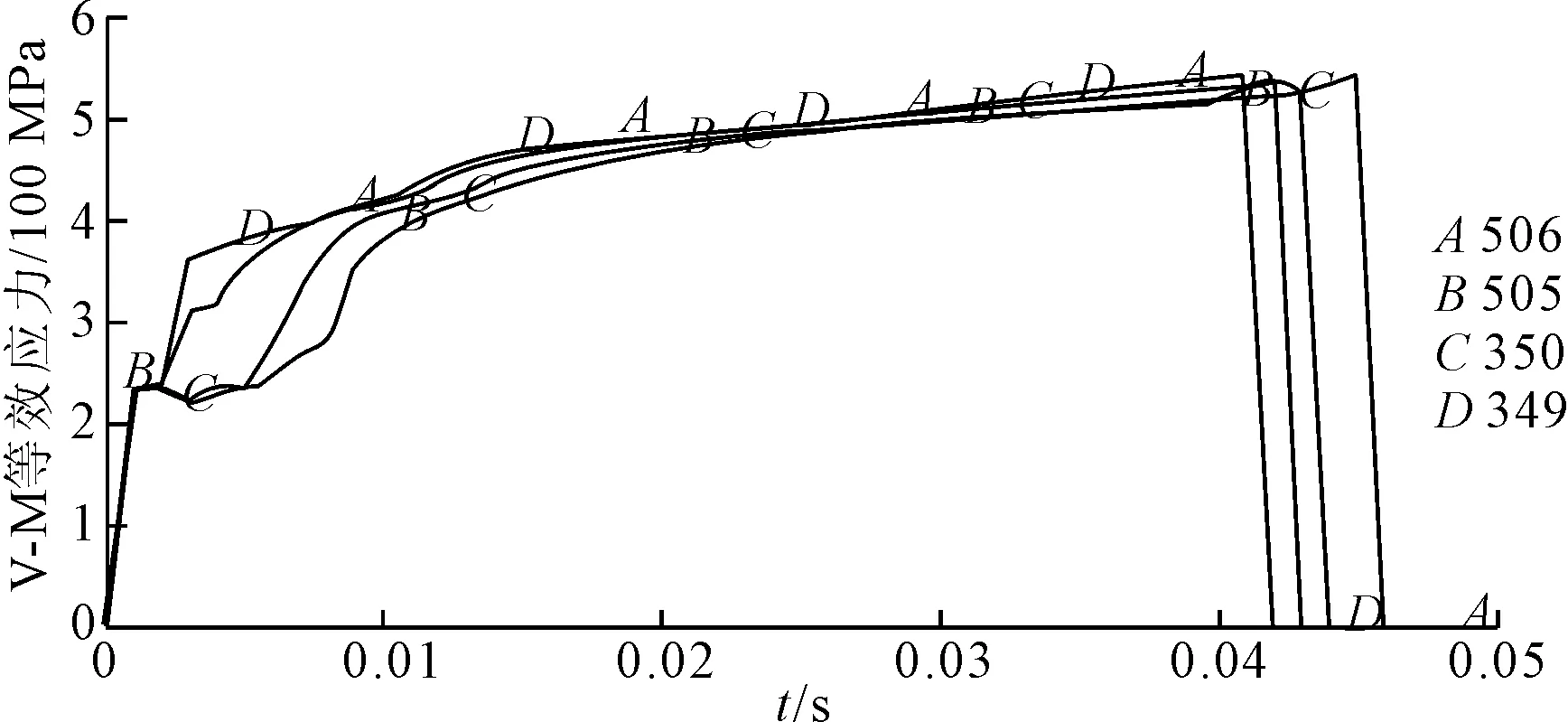
图8 失效单元的应力-时间关系
之后钢材发生了塑性变形,单元的应变迅速增长,直到达到了预设的失效应变。

图9 失效单元的应变-时间关系
2.2 最大主应变失效准则
按照工程力学中的定义,各主应力和主应变之间存在如下关系:σ1>σ2>σ3和ε1>ε2>ε3。最大主应变是ε1,亦即数值最大的主应变。
选取*MAT123作为材料模型对梁结构进行模拟,设置最大主应变为其失效准则,其余设置与上相同,其应力变形云图见图10。

图10 最大主应变失效准则下梁的破坏形式
由图10可见,下侧单元由于其内部应变首先达到钢材的受拉极限而发生失效破坏,应力最大区域维持在梁跨中的上侧,该结果与实际实验结果相似。由于上侧单元所受的力为压力(即σ3),按照工程力学的定义,单元受压时其应力为负值,所以上侧单元的最大压应力是最小主应力,因此并不受最大主应变失效准则的制约。
选取梁下侧破坏的两个单元与上侧受压单元进行分析,单元位置及其编号见图11。
图12为单元的V-M应力-时间变化曲线,从图中可见,在大约0.045 s的时刻,下侧的两个单元先后破坏失效,而上侧的两个单元虽然其有效应力值与下侧单元的应力值十分接近,但是并没有发生破坏,反而在下侧单元失效之后还在继续增长。这也证明了以上的推论——上侧单元受压,其应力值为负。而选取的失效准则为最大主应变失效准则,并不会对受压单元的失效起到判决的作用,直至下侧单元失效向上扩展至上侧单元也受拉时,失效准则才起到判决作用。
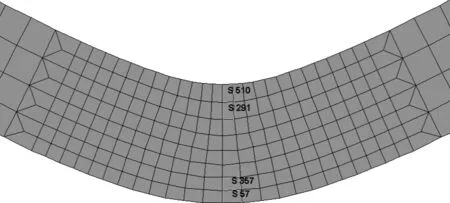
图11 失效单元位置及编号
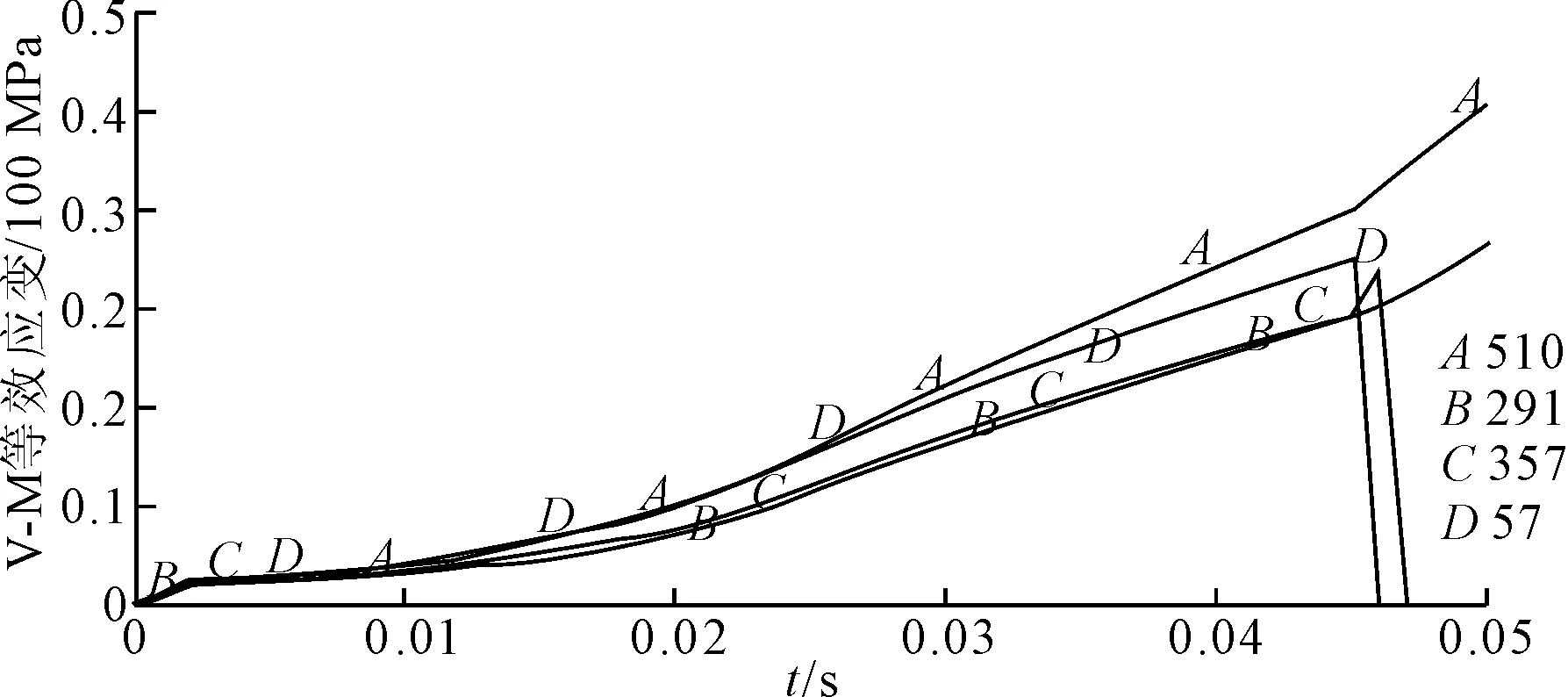
图12 失效单元的应力-时间关系曲线
图13为单元的V-M等效应变-时间曲线,可以看出与之前相似的推论,在达到了钢材的屈服极限之后,应变开始迅速增长,在大约0.045 s 时刻,下侧两个单元失效,而上侧两个单元的应变值继续增长。
图14为单元最大主应力-时间曲线,可见,当梁开始弯曲时,下侧两个单元(曲线C和D)的最大主应力迅速增长;在0.003 s之后过了结构的弹性阶段与屈服阶段,进入了强化阶段,并且一直呈增长趋势;0.045 s之后,由于其最大主应变达到了预设值,单元失效。而上侧的两个单元,其最大主应力基本维持在0(曲线G和H),从最小主应力-时间曲线上可以看到上侧两个单元的主应力变化情况,结果与之前的推论完全一致。

图14 失效单元的最大主应力与最小主应力曲线
2.3 厚度方向应变失效准则
厚度方向应变失效准则是指当结构受力变形时,以单元厚度方向的变化值除以原厚度值这一应变值作为单元失效与否的衡量标准,该准则仅对单元受拉导致的厚度变薄这种受力情况起衡量作用,对于单元受压力变厚的情况失效。
下面讨论以厚度方向应变作为失效准则对梁弯曲模拟结果的影响,设置厚度方向失效应变为0.05,其它设置与以上相似,进行有限元模拟。图15为梁的有效应力及变形云图。
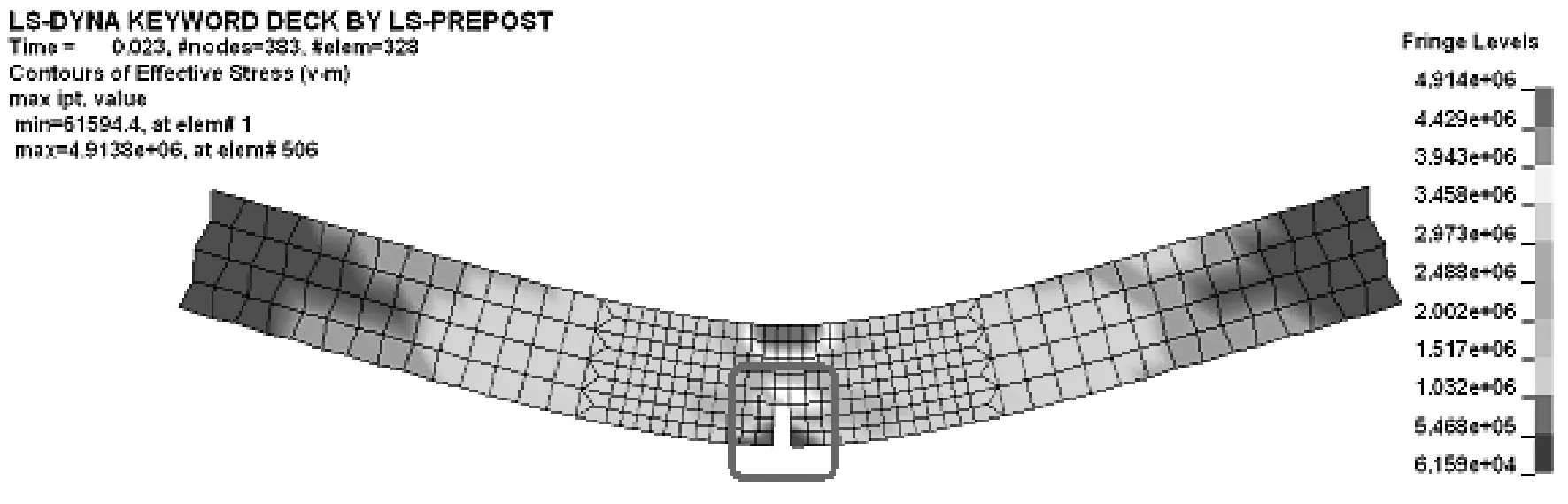
图15 厚度应变失效准则下的梁破坏形式
从图15中可见,梁跨中下边缘的单元由于受到拉应力而变薄,首先发生破坏,这说明厚度方向的失效应变也能够反映出梁的真实破坏特性,梁跨中上侧单元由于受到压力作用变厚,因而不会失效。其V-M应力应变关系曲线,最大主应力关系曲线与以上相似。
需要强调的是,这种失效准则只对shell单元有效。从理论上解释,对于shell单元,厚度方向即是单元的法线方向,当应变超出设定的失效准则后自然会发生破坏,而对于solid单元,由于单元本身的三维性,无法确切指定它的厚度方向。
3 分析总结

(6)
在任意应力状态下,形状改变比能为
(7)
整理后得
(8)
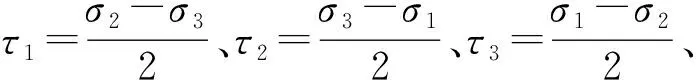
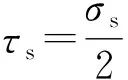
(9)
式(9)是根据形状改变比能理论建立的屈服准则的另一种表达形式。由此可以看出,这个理论在本质上仍然认为切应力是使材料屈服的决定性因素。它只适用于材料受拉极限与受压极限相同的材料,而在实际工程中,钢材的受压极限大都远大于受拉极限,所以单纯用这种失效准则来模拟材料的失效不准确且不可信。
2)最大主应变失效准则与厚度方向应变失效准则。最大主应变失效准则能够描述出结构受力方向对单元失效的影响,对于某些简单的结构,该准则能够较准确地模拟出真实失效情况,但是工程力学的应力定义考虑到了方向的影响,亦即数值有正负之分,最大主应力与其它两个主应力相比只是数值上的最大值,所以这种失效准则也有其局限性。厚度方向应变失效准则仅适用于shell单元,它是基于几何的角度考虑的,针对一个单元,在受力变形过程中,它的体积是不会发生变化的,厚度方向的应变对其单元是否会发生破坏具有一定的衡量性,而且多年的实践也证明,金属材料发生破坏最终是由于颈缩引起的,也即板厚变薄至一定程度,厚度方向应变超出了一定的范围导致的。所以它有着V-M等效应变失效和最大主应力失效所不可替代的优势。
基于以上各种失效准则的优缺点,可以将各种失效模式进行合理的搭配,以更好地模拟出真实情况下结构的受力破坏情况。由于厚度方向应变准则综合考虑了单元各方向受拉导致的厚度变薄失效,而主应变失效准则侧重于最大主应变方向的失效,所以厚度应变可作为主要的衡量标准。对于海洋工程用钢,根据其受拉极限远小于其受压极限的特点,可以选用厚度应变失效准则作为判别材料受拉破坏的标准,再选用V-M失效准则和主应变失效准则作为辅助判别准则,最终模拟出更加准确的结果。
[1] 陈惠发,A ·F·萨里普.弹性和塑性力学[M].北京:中国建筑出版社,2003.
[2] LESHAN ZHANG, EGGE E D, BRUHNS H. Approvalprocedure concept for alternative arrangements [D]. ICCGS, 2004.
